并查集

标签：return   就是   查询   while   并集   含义   数组   images   集合   

一、定义

并查集是一种树形的数据结构，用于处理一些不相交集合的合并以及查询问题。

二、操作

1、void make_set(int n)

含义：有n个元素，把这n个元素初始化成n个集合，每个集合包含1个元素。

2、int find_root(int x)

含义：查找元素x所在的集合，返回集合的根结点。通过查找两个元素的根结点是否相同，可以判断两个元素是否属于同一个集合。

3、void union_set(int a, int b)

含义：合并两个不相交的集合。

三、举例

假设有3个元素，编号分别为1,2,3，则进行初始化make_set后，这3个元素形成了3个集合{1},{2},{3},集合之间互不相交，对应的树如下图所示：

可以看到3个元素形成了3颗独立的树，每颗树只包含一个根结点。我们使用数组p[x]来表示结点x的父结点，若x为根结点，则令p[x]=-1（或者令p[x]=x），所以有p[1]=-1,p[2]=-1,p[3]=-1。合并集合则是将一棵树的根结点变成另一颗树的孩子结点，合并集合{1},{2}后，对应的数如下所示：

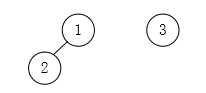
此时有p[1]=-1,p[2]=1,p[3]=-1。再将集合{3}与集合{1,2}合并，则有

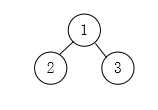
此时p[1]=-1，普p[2]=1,p[3]=1，3个集合最终合并成了一个集合。

四、优化

并查集最初的状态时一个个不相交的集合，如果只是简单的合并而不采取任何优化，那么树高可能会不断增加，最坏的情况是一棵树退化成了一条链，树高越高，查找根结点所花费的时间也就越长我们希望树应该尽可能的低，可以使用下面两种方法来进行优化：

1、路径压缩

在查找某结点x的根结点的过程中，将结点x与根结点和x之间的所有结点都直接指向根结点，这就是路径压缩。如下图：

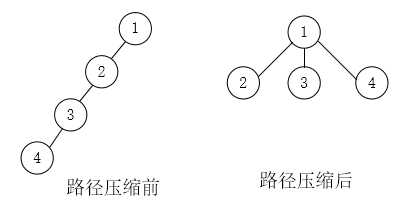
代码实现（递归）：

//查找根结点时路径压缩，递归实现
int find_root(int x)
{
    if(p[x] == -1)
        return x;
    else 
    {
        int t = find_root(p[x]);
        p[x] = t;
        return t;
    }
}

代码实现（非递归）：

//查找根结点时路径压缩，非递归实现
int find(int x)
{
    int k, j, r;
    r = x;
    while(r != parent[r])     //查找跟节点
        r = parent[r];      //找到跟节点，用r记录下
    k = x;        
    while(k != r)             //非递归路径压缩操作
    {
        j = parent[k];         //用j暂存parent[k]的父节点
        parent[k] = r;        //parent[x]指向跟节点
        k = j;                    //k移到父节点
    }
    return r;         //返回根节点的值            
}

2、按秩合并

按秩合并即将元素少的集合合并到元素多的集合中，这样有利于降低树高。

并查集

标签：return   就是   查询   while   并集   含义   数组   images   集合   

原文地址：http://www.cnblogs.com/sench/p/7953768.html