[POJ2409]Let it Bead - Polya定理

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It‘s a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced. 

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

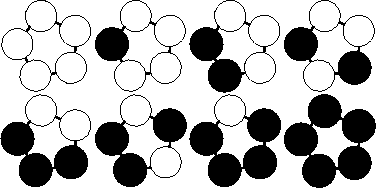For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0

1
2
3
5
8
13
21

题目大意
给出一串长为s的环，用c种颜色染色，可以翻转可以旋转，问有多少种不同的，即两两之间不能通过翻转或旋转得到的染色方法？

题解

看到这种题目，便想到了Polya定理(What‘s that?)。
如果不知什么是置换以及Polya定理，请戳上面的链接。

先考虑旋转的置换：
共n个置换
对于翻转m次(翻转一次就是翻360°/n，或第k+m个元素变为第k个元素的值）,一共有gcd(n,m)个循环节(1≤m≤n）
我们记S1=∑sgcd(n,m) (1≤m≤n）

接着考虑翻转的置换：
能发现一共也是n个置换
其次可以发现，偶数和奇数翻转的情况不一样
那么我们分类讨论

首先讨论最简单的奇数：
那当然是从每个点对半切开

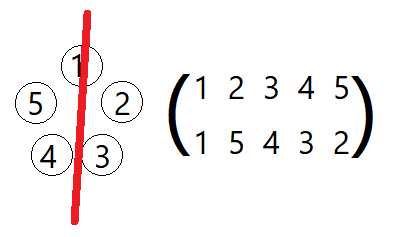
然后可以容易地发现对于每个点都有(n+1)/2个置换
那么我们记S2=n*s(n+1)/2

然后是偶数的情况
类似于奇数
但是有两种情况
1：从相对的两点切开，共n/2个置换，每个有(n+2)/2个循环节
2：切开后两边都是n/2个点，共n/2个置换，每个有n/2个循环节
那么我们记S2=n/2*s(n+2)/2　+　n/2*sn/2=(s+1)*n/2*sn/2

根据公式

可以算出最终的答案
其中|G|=2n,右边括号里边的和即之前的S1+S2
Ans=(S1+S2)/2n

代码如下：

 1 #include <iostream>
 2 #include <cstdio>
 3 using namespace std;
 4 #define LLI long long
 5 int gcd(int a,int b){
 6     return b==0?a:gcd(b,a%b);
 7 }
 8 int fastpow(int a,int b){int res=1;
 9 for(;b;b>>=1,a=a*a)if(b&1)res=a*res;return res;}
10 int main(){
11     int a,b;LLI ans;
12     while(scanf("%d%d",&a,&b)==2){
13         if(a==0&&b==0)break;
14         ans=0;
15         for(int i=1;i<=b;++i)ans+=fastpow(a,gcd(i,b));
16         if(b&1)ans+=1LL*b*fastpow(a,b+1>>1);
17         else ans+=1LL*(a+1)*(b>>1)*fastpow(a,b>>1);
18         ans/=b<<1;
19         printf("%lld\n",ans);
20     }
21     return 0;
22 }

代码写的有点丑……