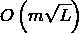标签:相等 hash pool 维护 应该 ada 并且 cond har
Description
火星人最近研究了一种操作:求一个字串两个后缀的公共前缀。比方说,有这样一个字符串:madamimadam,
我们将这个字符串的各个字符予以标号:序号: 1 2 3 4 5 6 7 8 9 10 11 字符 m a d a m i m a d a m 现在,
火星人定义了一个函数LCQ(x, y),表示:该字符串中第x个字符开始的字串,与该字符串中第y个字符开始的字串
,两个字串的公共前缀的长度。比方说,LCQ(1, 7) = 5, LCQ(2, 10) = 1, LCQ(4, 7) = 0 在研究LCQ函数的过程
中,火星人发现了这样的一个关联:如果把该字符串的所有后缀排好序,就可以很快地求出LCQ函数的值;同样,
如果求出了LCQ函数的值,也可以很快地将该字符串的后缀排好序。 尽管火星人聪明地找到了求取LCQ函数的快速
算法,但不甘心认输的地球人又给火星人出了个难题:在求取LCQ函数的同时,还可以改变字符串本身。具体地说
,可以更改字符串中某一个字符的值,也可以在字符串中的某一个位置插入一个字符。地球人想考验一下,在如此
复杂的问题中,火星人是否还能够做到很快地求取LCQ函数的值。
Input
第一行给出初始的字符串。第二行是一个非负整数M,表示操作的个数。接下来的M行,每行描述一个操作。操
作有3种,如下所示
1、询问。语法:Qxy,x,y均为正整数。功能:计算LCQ(x,y)限制:1<=x,y<=当前字符串长度。
2、修改。语法:Rxd,x是正整数,d是字符。功能:将字符串中第x个数修改为字符d。限制:x不超过当前字
符串长度。
3、插入:语法:Ixd,x是非负整数,d是字符。功能:在字符串第x个字符之后插入字符d,如果x=0,则在字
符串开头插入。限制:x不超过当前字符串长度
Output
对于输入文件中每一个询问操作,你都应该输出对应的答案。一个答案一行。
Sample Input
madamimadam
7
Q 1 7
Q 4 8
Q 10 11
R 3 a
Q 1 7
I 10 a
Q 2 11
Sample Output
5
1
0
2
1
HINT
1、所有字符串自始至终都只有小写字母构成。
2、M<=150,000
3、字符串长度L自始至终都满足L<=100,000
4、询问操作的个数不超过10,000个。
对于第1,2个数据,字符串长度自始至终都不超过1,000
对于第3,4,5个数据,没有插入操作。
题目大意 支持插入、修改字符,并且询问两个位置开始的最长公共前缀。
Solution 1 平衡树
用平衡树维护区间的Hash值,对于询问操作,二分答案,然后再区间查询check。
(比较懒,改天再写这个做法)
Solution 2 块状链表
对于普通的数组,插入最坏O(n),对于普通的链表,插入最坏O(n)。
导致链表速度慢的原因是找到插入位置,导致数组插入慢的原因是挪动元素。
考虑一个数据就够能够解决这两个问题。
我们对链表进行分块就能很好地解决这个问题。
不过要注意一点:当块大小足够大时,需要分裂,否则会容易被卡。
对于这个问题,我的做法是如果插入的块满了,并且下一个块也满了才新开一块放溢出的元素。
现在考虑查询操作。
每一块维护前缀Hash值和后缀Hash值,然后每次考虑向前 个元素,比较这一段的Hash值,如果它们相等就往前跳,如果不相等就一个字符一个字符地往前跳,直到某个字符不相等。
个元素,比较这一段的Hash值,如果它们相等就往前跳,如果不相等就一个字符一个字符地往前跳,直到某个字符不相等。
注意一个问题,就是查询的两个起始位置相等,特判一下就好。
然后注意插入的边界问题。
总时间复杂度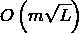
(我本来天真地以为这个会比平衡树好写,然后我发现我想多了。。)
Code
1 /**
2 * bzoj
3 * Problem#1014
4 * Accepted
5 * Time: 3972ms
6 * Memory: 3824k
7 */
8 #include <bits/stdc++.h>
9 using namespace std;
10 typedef bool boolean;
11
12 const int cs = 350;
13 const int base = 200379;
14 int powb[100005];
15
16 typedef class Chunk {
17 public:
18 Chunk *suf;
19 int s;
20 char str[cs + 5];
21 int psh[cs + 5];
22 int ssh[cs + 5];
23
24 Chunk():suf(NULL), s(0) { }
25 Chunk(Chunk* org, int s):suf(org), s(s) { }
26
27 static Chunk* alloc();
28
29 void maintain() {
30 psh[0] = ssh[s + 1] = 0;
31 for(int i = 1; i <= s; i++)
32 psh[i] = psh[i - 1] + str[i] * powb[i - 1];
33 for(int i = s; i; i--)
34 ssh[i] = ssh[i + 1] * base + str[i];
35 }
36
37 void insert(int p, char x) {
38 for(int i = s + 1; i > p; i--)
39 str[i] = str[i - 1];
40 str[p] = x;
41 if(full()) {
42 Chunk* nc = suf;
43 if(suf->full()) {
44 nc = alloc();
45 nc->suf = suf;
46 suf = nc;
47 }
48 nc->insert(1, str[s + 1]);
49 } else s++;
50 if(p <= s)
51 maintain();
52 }
53
54 void modify(int p, char x) {
55 str[p] = x;
56 maintain();
57 }
58
59 boolean full() {
60 return s == cs;
61 }
62 }Chunk;
63
64 Chunk pool[650];
65 Chunk *top = pool;
66
67 Chunk* Chunk::alloc() {
68 return top++;
69 }
70
71 typedef pair<Chunk*, int> pci;
72 #define fi first
73 #define sc second
74
75 int m;
76 Chunk nsta = Chunk(&nsta, cs), nend = Chunk(&nend, cs);
77 char str[100005];
78
79 inline void init() {
80 nsta.suf = &nend;
81 powb[0] = 1;
82 for(int i = 1; i <= 100002; i++)
83 powb[i] = powb[i - 1] * base;
84 memset(nend.psh, -1, sizeof(nend.psh));
85
86 gets(str + 1);
87 scanf("%d", &m);
88
89 int fin = 1;
90 Chunk* pc = &nsta, *nc;
91 while(str[fin]) {
92 nc = Chunk::alloc();
93 nc->suf = pc->suf;
94 pc->suf = nc;
95 for(nc->s = 0; str[fin] && nc->s < cs; )
96 nc->str[++nc->s] = str[fin++];
97 nc->maintain();
98 pc = nc;
99 }
100 }
101
102 pci findc(int pos) {
103 int skip = 0;
104 pci rt(nsta.suf, 0);
105 while(skip + rt.fi->s < pos) {
106 skip += rt.fi->s;
107 rt.fi = rt.fi->suf;
108 }
109 rt.sc = pos - skip;
110 return rt;
111 }
112
113 int getHash(pci p, pci& nxt) {
114 int skip = 0, rt = 0;
115 rt = p.fi->ssh[p.sc];
116 skip = p.fi->s - p.sc + 1;
117 p.fi = p.fi->suf;
118 while(skip + p.fi->s < cs) {
119 rt += powb[skip] * p.fi->psh[p.fi->s];
120 skip += p.fi->s;
121 p.fi = p.fi->suf;
122 }
123 nxt = pci(p.fi, cs - skip + 1);
124 if(nxt.sc > nxt.fi->s) {
125 nxt.sc -= nxt.fi->s;
126 nxt.fi = nxt.fi->suf;
127 }
128 rt += powb[skip] * p.fi->psh[cs - skip];
129 return rt;
130 }
131
132 void getnext(pci &p) {
133 if(p.sc == p.fi->s)
134 p.sc = 1, p.fi = p.fi->suf;
135 else
136 p.sc++;
137 }
138
139 void debugout() {
140 Chunk* p = nsta.suf;
141 while(p != &nend) {
142 puts(p->str + 1);
143 p = p->suf;
144 }
145 }
146
147 inline void solve() {
148 char buf[5];
149 int x, y, rt;
150 pci p1, p2, pn1, pn2;
151 // debugout();
152 while(m--) {
153 scanf("%s%d", buf, &x);
154 if(buf[0] == ‘Q‘) {
155 scanf("%d", &y);
156 if(x != y) {
157 rt = 0, p1 = findc(x), p2 = findc(y);
158 while(getHash(p1, pn1) == getHash(p2, pn2)) p1 = pn1, p2 = pn2, rt += cs;
159 while(p1.fi->str[p1.sc] == p2.fi->str[p2.sc]) {
160 getnext(p1);
161 getnext(p2);
162 rt++;
163 }
164 } else {
165 p1 = findc(x);
166 rt = p1.fi->s - p1.sc + 1;
167 p1.fi = p1.fi->suf;
168 while(p1.fi != &nend) {
169 rt += p1.fi->s;
170 p1.fi = p1.fi->suf;
171 }
172 }
173 printf("%d\n", rt);
174 } else if(buf[0] == ‘R‘) {
175 scanf("%s", buf);
176 p1 = findc(x);
177 p1.fi->modify(p1.sc, buf[0]);
178 } else {
179 scanf("%s", buf);
180 p2 = p1 = findc(x);
181 getnext(p1);
182 if(p1.fi != &nend)
183 p1.fi->insert(p1.sc, buf[0]);
184 else
185 p2.fi->insert(p2.sc + 1, buf[0]);
186 }
187 }
188 }
189
190 int main() {
191 init();
192 solve();
193 return 0;
194 }
bzoj 1014 火星人prefix - 链表 - 分块
标签:相等 hash pool 维护 应该 ada 并且 cond har
原文地址:http://www.cnblogs.com/yyf0309/p/7965692.html

 个元素,比较这一段的Hash值,如果它们相等就往前跳,如果不相等就一个字符一个字符地往前跳,直到某个字符不相等。
个元素,比较这一段的Hash值,如果它们相等就往前跳,如果不相等就一个字符一个字符地往前跳,直到某个字符不相等。