标签:区别 detail 定义 无法 应该 就是 总结 line 存在
我是按照这里的思路来的。这个博文只是感性理解。
关于递归树,这篇博文讲的很好,我只是给自己总结一下。
定义vis数组,在dfs连通图时赋予它们不同的含义:
一个连通图,一定可以表示成一个递归树,加上一些边。这些边的种类有:
一个强连通的东西,必定在一棵递归树上,不会分散到多个上。不然那东西就不连通了,想要强连通更是不可能。
对了,如果将dfs访问到的时间,给递归树上的点编号,一个点的祖先的编号一定比这个点小。
还记得tarjan里,判断一个点是否出栈的依据吗?就是\(dfn[u]=low[u]\)。这意味着在u的子结点中,没有回往u以上的边,不然\(low[u]<dfn[u]\)。所以根据tarjan算法,如果u出栈,出栈的东西中编号最小的就是u。出栈的东西应该类似于这样(没画有向边,所以脑补吧):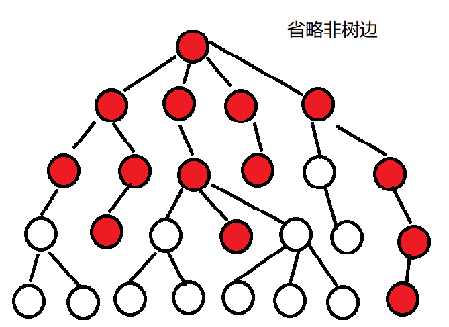
也就是说,一个节点只有间接连向u,才能和u组成一个强连通的东西。这导致强连通分量在递归树上,其实就是一堆链的集合体,也就是树。
重点来了。如果tarjan搞出来的东西中,有一些点不和其它点强连通,说明它不能间接连向u,而是会间接连向u的一个儿子v。如果\(low[v]<dfn[v]\),这个点又可以间接连向\(low[v]\)...,以此类推,最终连向一个可以出栈的点,那个点u的是儿子。这就证明了,一次出栈搞出来的东西,和u都是强连通的。
这个标题和前面哪一个的区别是什么呢?就是一个是“东西”,一个是“分量”。分量意味着它大的不能再大了。所以这里要证明(弥天大雾,其实我这个根本不算证明)的,就是一次tarjan搞出来的,最小结点为u的强连通分量中,不会有其它点被遗漏。至于这个证明,我贴一个引用过来:
假设出栈的部分不完整,则本应该在这次出栈的点可能存在于栈的哪些部分呢?
1.之前出栈的部分
2.还没有入栈的部分
3.还没有出栈的部分
首先看2,不可能。因为假如没有入栈,说明这些点没有在这棵深度优先搜索树中,假如这些点在本该在该强连通分量中,则和定理1相违背,所以情况2中不可能包含本应该出栈的强连通分量中的点。再看3,也不可能。3中的点的dfn 和 low都分别小于本次出栈的点的dfn和low,也就说明本次出栈的点都无法访问到还没有出栈的点,所以情况3中不可能包含本应该出栈的强连通分量中的点。最后看情况1,其实情况1和情况3是类似的,之前出栈的部分A如果和本次出栈的强连通分量B可以组成更大的强连通分量,这就等价于,以之前出栈的强连通分量A为视角,亦是说A是不完整的,A中缺少的部分在还未出栈的节点和还没有访问的节点之中。这和之前的情况2,情况3推导矛盾,所以,情况1也不可能。
标签:区别 detail 定义 无法 应该 就是 总结 line 存在
原文地址:http://www.cnblogs.com/MyNameIsPc/p/7966152.html