标签:比较 microsoft family class nbsp stream span arp clear
T1

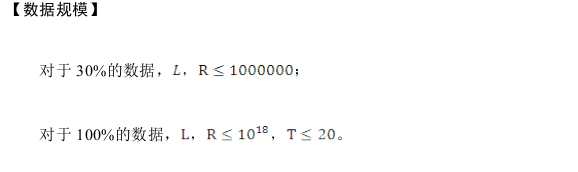
卡死在T1。
打了两个小时数位dp,结果tmd是道结论题。
∵d(x)==x%9
∴喜欢的数一定可以写成(x*9+b)*b==9*x*b+b*b的形式
b从1~9,把d*d按模9的余数分类算一下,然后容斥一下即可。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
#define LL long long
LL calc(LL x) {
LL res=0,a,b;
if(x>=1) res+=(x-1)/9+1;
a=x>=4?(x-4)/18+1:0; b=x>=49?(x-49)/63+1:0;
res=res+a+b-a/7;
a=x>=16?(x-16)/36+1:0LL; b=x>=25?(x-25)/45+1:0;
res=res+a+b-a/5;
a=x>=9?(x-9)/27+1:0LL; b=x>=36?(x-36)/54+1:0;
if(x>=81) res+=x/81;
res=res+a+b-a/2;
return res;
}
int main()
{
int T;
LL l,r;
scanf("%d",&T);
while(T--)
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",calc(r)-calc(l-1));
}
return 0;
}
忘了return然后wa成傻逼
T2

一个因为数据水可以过的歪解
因为可以发现最小路径上显然每个点只会经过一次
只要只要不从从一出去的这条路再走回来即可
枚举每条出去的边,删掉它的反向边,跑spfa
数据很水,加个slf优化就过了90.第一个点比较毒不管。
//Achen
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<vector>
#include<queue>
#include<ctime>
#include<cmath>
const int N=10005;
const int M=400007;
typedef long long LL;
using namespace std;
int n,m;
template<typename T> void read(T &x) {
char ch=getchar(); x=0; T f=1;
while(ch!=‘-‘&&(ch<‘0‘||ch>‘9‘)) ch=getchar();
if(ch==‘-‘) f=-1,ch=getchar();
for(;ch>=‘0‘&&ch<=‘9‘;ch=getchar()) x=x*10+ch-‘0‘; x*=f;
}
int ecnt=1,fir[N],nxt[M],to[M],val[M];
void add(int u,int v,int w) {
nxt[++ecnt]=fir[u]; fir[u]=ecnt; to[ecnt]=v; val[ecnt]=w;
}
deque<int>que;
int vis[N],dis[N];
int spfa(int idd) {
memset(dis,127/3,sizeof(dis));
dis[to[idd]]=0; vis[to[idd]]=1;
que.push_back(to[idd]);
while(!que.empty()) {
int x=que.front();
que.pop_front();
vis[x]=0;
for(int i=fir[x];i;i=nxt[i]) if(i!=(idd^1)) {
int y=to[i];
if(dis[y]>dis[x]+val[i]) {
dis[y]=dis[x]+val[i];
if(!vis[y]) {
vis[y]=1;
if(!que.empty()) {
int tp=que.front();
if(dis[y]<dis[tp]) que.push_front(y);
else que.push_back(y);
}
else que.push_back(y);
}
}
}
}
return val[idd]+dis[1];
}
void work() {
int ans=1e9+7;
for(int i=fir[1];i;i=nxt[i]) {
ans=min(ans,spfa(i));
}
printf("%d\n",ans);
}
void init() {
read(n); read(m);
for(int i=1;i<=m;i++) {
int u,v,w,ww;
read(u);
read(v);
read(w);
read(ww);
add(u,v,w);
add(v,u,ww);
}
}
int main() {
#ifdef DEBUG
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
init();
work();
return 0;
}
/*
3 3
1 2 2 1
2 3 4 5
3 1 3 2
*/
T3
好像T2,T3搞反了,无所谓了。

二分答案跑有上下界的网络流。
设现在check的答案为ans
源点向每一行连上界为sumh[i]+ans,下界为max(sumh[i]-ans,0)的边
每一行向每一列连上界R下界L的边
每一列向汇点连上界为suml[i]+ans,下界为max(suml[i]-ans,0)的边
注意超级源点和超级汇点的处理方法,每个点是出流减入流,然后记得汇点向源点连inf的边
最后判断超级源点的边是否满流即可
又验证了一下ISAP的优越性
//Achen
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<vector>
#include<queue>
#include<ctime>
#include<cmath>
#define inf 0x7fffffff
const int N=405;
typedef long long LL;
using namespace std;
int n,m,L,R,tot,lim,a[N][N],b[N][N],sumh[N],suml[N];
template<typename T> void read(T &x) {
char ch=getchar(); x=0; T f=1;
while(ch!=‘-‘&&(ch<‘0‘||ch>‘9‘)) ch=getchar();
if(ch==‘-‘) f=-1,ch=getchar();
for(;ch>=‘0‘&&ch<=‘9‘;ch=getchar()) x=x*10+ch-‘0‘; x*=f;
}
struct edge {
int from,to,cap,flow,nxt;
edge() {}
edge(int from,int to,int cap,int flow,int nxt):from(from),to(to),cap(cap),flow(flow),nxt(nxt) {}
}e[N*N*2];
int ecnt=1,fir[N],cur[N];
void add(int u,int v,int w) {
e[++ecnt]=edge(u,v,w,0,fir[u]); fir[u]=ecnt;
e[++ecnt]=edge(v,u,0,0,fir[v]); fir[v]=ecnt;
}
int d[N],c[N],p[N],ve[N];
queue<int>que;
void bfs(int s,int t) {
for(int i=1;i<=tot;i++) d[i]=tot,c[i]=0;
d[t]=0; que.push(t);
while(!que.empty()) {
int x=que.front();
que.pop();
for(int i=fir[x];i;i=e[i].nxt) {
int y=e[i].to;
if(d[y]==tot&&e[i].flow==e[i].cap) {
d[y]=d[x]+1;
que.push(y);
}
}
}
return;
}
int cal(int s,int t) {
int res=inf;
for(int x=t;x!=s;x=e[p[x]].from)
res=min(res,e[p[x]].cap-e[p[x]].flow);
for(int x=t;x!=s;x=e[p[x]].from) {
e[p[x]].flow+=res;
e[p[x]^1].flow-=res;
}
return res;
}
int ISAP(int s,int t) {
bfs(s,t);
int res=0;
for(int i=1;i<=tot;i++) cur[i]=fir[i],c[d[i]]++;
for(int x=s;d[x]<tot;) {
if(x==t) {
res+=cal(s,t);
x=s;
}
int ok=0;
for(int &i=cur[x];i;i=e[i].nxt) {
int y=e[i].to;
if(d[y]+1==d[x]&&e[i].cap>e[i].flow) {
p[x=y]=i; ok=1; break;
}
}
if(!ok) {
cur[x]=fir[x];
int M=tot;
for(int i=fir[x];i;i=e[i].nxt) {
int y=e[i].to;
if(e[i].cap>e[i].flow) M=min(M,d[y]+1);
}
if(M==tot) break;
if(!(--c[d[x]])) break;
c[d[x]=M]++;
if(x!=s) x=e[p[x]].from;
}
}
return res;
}
void clear() {
memset(fir,0,sizeof(fir));
ecnt=1; lim=0;
memset(ve,0,sizeof(ve));
}
int check(int ans) {
clear();
int s=n+m+1,t=s+1,ss=t+1,tt=ss+1;
tot=tt;
for(int i=1;i<=n;i++) {
int up=(ans+sumh[i]),dn=max(0,sumh[i]-ans);
add(s,i,up-dn);
ve[s]+=dn;
ve[i]-=dn;
}
for(int i=1;i<=m;i++) {
int up=(ans+suml[i]),dn=max(0,suml[i]-ans);
add(n+i,t,up-dn);
ve[n+i]+=dn;
ve[t]-=dn;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) {
int up=R,dn=L;
add(i,n+j,up-dn);
ve[i]+=dn;
ve[n+j]-=dn;
}
for(int i=1;i<=tot;i++) {
if(ve[i]>0) add(i,tt,ve[i]);
else if(ve[i]<0) { add(ss,i,-ve[i]); lim-=ve[i];}
}
add(t,s,inf);
return ISAP(ss,tt)>=lim;
}
void work() {
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sumh[i]+=a[i][j];
for(int j=1;j<=m;j++)
for(int i=1;i<=n;i++)
suml[j]+=a[i][j];
int l=0,r=2e5,ans=r;
while(l<=r) {
int mid=(l+r)>>1;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
check(ans);
printf("%d\n",ans);
for(int i=1;i<=n;i++)
for(int j=fir[i];j;j=e[j].nxt)
if(e[j].to>=n+1&&e[j].to<=n+m)
b[i][e[j].to-n]=e[j].flow+L;
for(int i=1;i<=n;i++) {
for(int j=1;j<m;j++)
printf("%d ",b[i][j]);
printf("%d",b[i][m]);
printf("\n");
}
}
void init() {
read(n); read(m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
read(a[i][j]);
read(L); read(R);
}
int main() {
#ifdef DEBUG
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
init();
work();
return 0;
}
/*
2 2
0 1
2 1
0 1
*/
标签:比较 microsoft family class nbsp stream span arp clear
原文地址:http://www.cnblogs.com/Achenchen/p/7976592.html