标签:第一个 base 不同的 缓冲区 col ase cout idt count
代码实现:

#include <bits/stdc++.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 #define LIST_INIT_SIZE 100 //线性表初始空间分配量 #define LISTINCREMENT 10 //线性表空间分配的增量 using namespace std; typedef int Status; typedef int ElemType; typedef struct LNode{ ElemType *elem; //存储空间的基地址 int lenght; //当前的长度 int listsize; //当前分配的存储容量 }SqList; // 初始化 线性表 空表 Status initList(SqList &L, int lenght){ if (lenght == 0) lenght = LIST_INIT_SIZE; L.elem = (ElemType *)malloc(lenght * sizeof(ElemType)); if(!L.elem) exit(OVERFLOW); //分配存储空间失败 L.lenght = 0; //初始空表长度为0 L.listsize = lenght ;//初始存储容量为100 return OK; } // 在 i 位置 插入 e Status insertList(SqList &L, ElemType e, int i){ ElemType *p, *q; if(i<0 ||i > L.lenght) return ERROR; //i值不合法 if (L.lenght >= L.listsize) { ElemType *newbase = (ElemType *)realloc(L.elem ,(L.listsize +LISTINCREMENT)*sizeof(ElemType)); if(!newbase) return OVERFLOW; //存储分配失败 L.elem = newbase; //新基值 L.listsize += LISTINCREMENT; //增加存储容量 } q = &L.elem[i]; //q为插入的位置 for (p = &L.elem[L.lenght]; p>=q; --p) { *p = *(p-1); //i元素之后的元素往后移动 } *q = e; //插入e L.lenght +=1; return OK; } /* void ListInsert(SqList *L,int i,ElemType e) // 插入操作的第二写法 //在线性表L的第i个位置插入新元素e { if(L->lenght==100) { printf("线性表已满\n"); return; } if(i<1||i>L->lenght+1) { printf("插入位置出错\n"); return; } for(int k=L->lenght;k>=i;k--) { L->data[k]=L->data[k-1]; } L->data[i-1]=e; L->lenght++; } */ // 删除元素操作 Status deleteListElem(SqList &L, int i, ElemType &e){ int *p, *q; if(i<0 ||i > L.lenght) return ERROR; //i值不合法 q = &L.elem[i]; //被删除元素的位置为i,L.elem就是数组名, e = *q; //被删除元素的值赋值给e for (p = q; p< (L.elem + L.lenght); p++){ //元素左移 *p = *(p+1); } --L.lenght; return OK; } /*// 第二删除操作 void ListDelete(SqList *L,int i,ElemType *e) //删除线性表L中的第i个位置元素,并用e返回其值 { if(L->length==0) { printf("线性表为空\n"); return; } if(i<1||i>L->length) { printf("位置出错\n"); return; } *e=L->data[i-1]; for(int k=i;k<l->length;k++) { L->data[k-1]=L->data[k]; } L->length--; return; } */ // 线性表快速排序 int partition(SqList &L, ElemType low, ElemType high){ ElemType pivotkey = L.elem[low]; //枢轴记录关键字 while (low < high) { //从表的两端向中间扫描 while (low < high && L.elem[high] >= pivotkey ) --high;//高端位置扫描 L.elem[low] = L.elem[high]; //交换数据,小于pivotkey移到低端 L.elem[high] = pivotkey; while (low < high && L.elem[low] <= pivotkey ) ++low; //低端扫描 L.elem[high] = L.elem[low]; //交换数据 大于pivotkey移到高端 L.elem[low] = pivotkey; } return low; } //分治法 : void quickSort(SqList &L, ElemType low, ElemType high){ int pivot; if(low < high) { pivot = partition(L, low, high); quickSort(L, low, pivot -1); //低端子表排序 quickSort(L, pivot +1, high); //高端子表排序 } } // 线性表合并操作 void mergeList(SqList La, SqList Lb, SqList &Lc){ ElemType *pa, *pb, *pc; Lc.listsize = La.lenght + Lb.lenght; initList(Lc, Lc.listsize); //初始化LC\pc = Lc.elem; Lc.lenght = Lc.listsize; pc = Lc.elem; pa = La.elem; pb = Lb.elem; while (pa <= &La.elem[La.lenght -1] && pb <= &Lb.elem[Lb.lenght -1]){ if (*pa <= *pb) *pc++ = *pa++; else *pc++ = *pb++; } while(pa <= &La.elem[La.lenght -1]) *pc++ = *pa++; //插入La的剩余元素 while(pb <= &Lb.elem[Lb.lenght -1]) *pc++ = *pb++; //插入Lb的剩余元素 } // 打印操作 void printList(SqList L){ printf("当前值:"); for (int i =0; i<L.lenght;i++) { printf("%d ", *(L.elem+i)); // L.elem为首地址 } printf("\r\n"); } int main() { SqList La,Lb,Lc; ElemType e; int init,i; init = initList(La, LIST_INIT_SIZE); int data[6] = {5,3,6,2,7,4}; for (i=0; i<6;i++) { insertList(La, data[i], i); } printf("LA:\r\n"); printList(La); deleteListElem(La, 3, e ); printList(La); insertList(La, e, 3); printList(La); //排序 quickSort(La,0, La.lenght-1); printList(La); printf("LB:\r\n"); initList(Lb, LIST_INIT_SIZE); int Bdata[5] = {1,3,2,4,6}; for (i=0; i<5;i++) { insertList(Lb, Bdata[i], i); } //排序 quickSort(Lb,0, Lb.lenght-1); printList(Lb); mergeList(La, Lb, Lc); printList(Lc); }
顺序存储结构:
原理:使用数组,数组把线性表的数据元素存储在一块连续地址空间的内存单位中
特点:线性表中逻辑上相邻的数据元素在物理地址上也相邻。
优点:算法简单,存储密度大,空间单位利用效率高
缺点:需要预先确定数据元素的最大个数,并且插入和删除操作时需要移动较多的数据元素。(可简化为:插入或删除元素时不方便)
在顺序表中实现的基本运算:
·插入:平均移动结点次数为n/2;平均时间复杂度均为O(n)。
·删除:平均移动结点次数为(n-1)/2;平均时间复杂度均为O(n)。

#include <bits/stdc++.h> using namespace std; #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 #define LT(a,b) ((a)<(b)) #define N = 100 typedef int Status; typedef int ElemType; /* 链表的存储特点: 链表的存储方式也于此类似,下面讨论一下链表的特点: (1)数据元素的逻辑顺序和物理顺序不一定相同。 (2)在查找数据元素时,必须从头指针开始依次查找,表尾的指针域指向NULL。 (3)在特定的数据元素之后插入或删除元素,不需要移动数据元素,因此时间复杂度为 O(1)。 (4) 存储空间不连续,数据元素之间使用指针相连,每个数据元素只能访问周围的一个元素。 (5)长度不固定,可以任意增删。 */ typedef struct LNode{ ElemType data; struct LNode *next; }LNode, *LinkList; /************************************************************************/ /* 初始化链表 */ /************************************************************************/ Status initList(LinkList &L){ /*单链表的初始化*/ L = (LinkList)malloc(sizeof(LNode)); //申请一个头节点 if(!L) exit(OVERFLOW); //申请空间失败 L->next=NULL; //建立一个带都节点的空链表 return OK; /* 需要改变指针的指针,所以参数必须是引用或者是 *L: (*L) = (Lnode *)malloc(sizeof(Lnode)); (*L)->next=NULL; return 1; */ } /************************************************************************/ /* 创建链表 */ /************************************************************************/ void createList(LinkList L, int n){ /*单链表的初始化*/ if (!L) { initList(L); } ElemType data; LinkList p,q = L; printf("输入节点数据的个数%d:\r\n", n); for(int i = 0; i<n; i++) { p = (LinkList) malloc( sizeof(LNode)); //申请一个新节点 scanf("%d",&data); p->data = data; p->next = q->next; q->next = p; q = p; } } /************************************************************************/ /* 在第i位置插入e */ /************************************************************************/ Status insertList(LinkList L, ElemType e, int i){ LinkList s, p = L; int j = 0; while (p && j<i){ //寻找i节点 p = p->next; j++; } if (!p ||j >i) return ERROR; s = (LinkList) malloc(sizeof(LNode)); //生成新节点 s->data = e; s->next = p->next; //插入L中 p->next = s; return OK; } /************************************************************************/ /* 删除第i位置元素,并用e返回其值 */ /************************************************************************/ Status deleteListElem(LinkList L, int i, ElemType &e){ LinkList p, q; int j = 0; p = L; while (p && j<i){ p = p->next; ++j; } if (!p->next || j>i) return ERROR; //删除的位置不对 q = p->next; p->next = q->next; e = q->data; free(q); //释放节点 return OK; } /************************************************************************/ /* 插入排序 */ /************************************************************************/ void InsertSort(LinkList L) { LinkList list; /*为原链表剩下用于直接插入排序的节点头指针*/ LinkList node; /*插入节点*/ LinkList p; LinkList q; list = L->next; /*原链表剩下用于直接插入排序的节点链表*/ L->next = NULL; /*只含有一个节点的链表的有序链表。*/ while (list != NULL) { /*遍历剩下无序的链表*/ node = list, q = L; while (q && node->data > q->data ) { p = q; q = q->next; } if (q == L) { /*插在第一个节点之前*/ L = node; } else { /*p是q的前驱*/ p->next = node; } list = list->next; node->next = q; /*完成插入动作*/ } } /************************************************************************/ /* 合并两个线性表 */ /************************************************************************/ void mergeList(LinkList &La, LinkList &Lb, LinkList &Lc){ LinkList pa, pb, pc; pa = La->next; pb = Lb->next; Lc = pc = La; while (pa && pa) { if (pa->data > pb->data) { pc->next = pb; pc = pb; pb =pb->next; }else{ pc->next = pa; pc = pa; pa =pa->next; } } pc->next = pa? pa :pb; free(Lb); } /************************************************************************/ /* 打印list */ /************************************************************************/ void printList(LinkList L){ printf("当前值:"); LinkList p; p = L->next; while(p){ printf("%d ", p->data); p = p->next; } printf("\r\n"); } int main() { LinkList La,Lb,Lc; ElemType e; int init,i; printf("LA:\r\n"); initList(La); createList(La, 5); insertList(La, 7, 3); printList(La); deleteListElem(La, 3, e); printList(La); InsertSort(La); printList(La); printf("Lb:\r\n"); initList(Lb); createList(Lb, 4); InsertSort(Lb); printList(Lb); printf("Lc:\r\n"); initList(Lc); mergeList(La, Lb, Lc); printList(Lc); }
链式存储结构:
原理:把存放数据元素的结点用指针域构造成链。
特点:数据元素间的逻辑关系表现在结点的连接关系上
优点:不需要预先确定数据元素的最大个数,插入和删除操作是不需要移动数据元素(可简
化为:优点:插入或删除元素时很方便,使用灵活。
缺点:存储密度小,空间单位利用效率低
链表三节点区别:
·头指针:指向链表中第一个结点(或为头结点或为首元结点)的指针。
·头结点:链表的首元结点之前附设的一个结点。即头指针所指的不存放数据元素的第一个结点。
·首结点:链表中存储线性表中第一个数据元素的结点。
头结点的作用主要是使插入和删除等操作统一,在第一个元素之前插入元素和删除第一个结点不必另作判断。另外,不论链表是否为空,链表指针不变。

#include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int ElemType; typedef struct LNode { ElemType data; struct LNode *next; }LNode, *LinkList; /** * 操作结果:构造一个空的线性表L * @param L */ void InitList(LinkList *L) { *L = (LinkList)malloc(sizeof(struct LNode)); if (!*L) { exit(OVERFLOW); } (*L)->next = NULL; } /** * 初始条件:线性表 L存在 * 操作结果:销毁线性表 L * @param L */ void DestroyList(LinkList *L) { LinkList q; while (*L) { q = (*L)->next; free(*L); *L = q; } } /** * 初始条件:线性表 L 存在 * 操作结果:将 L 置为空表 * @param L */ void ClearList(LinkList L) { LinkList p, q; p = L->next; while (p) { q = p->next; free(p); p = q; } L->next = NULL; } /** * 初始条件:线性表 L 存在 * 操作结果:若 L 为空表,返回 TRUE,否则返回 FALSE * @param L * @return */ Status ListEmpty(LinkList L) { return L->next == NULL; } /** * 初始条件:线性表 L 存在 * 操作结果:返回 L 中的数据元素个数 * @param L * @return */ int ListLength(LinkList L) { int i = 0; LinkList p = L->next; while (p) { i++; p = p->next; } return i; } /** * 初始条件:线性表 L 存在,且 1 <= i <= ListLength(L) * 操作结果:用 e 返回 L 中第 i 个元素的值 * @param L * @param i * @param e * @return */ Status GetElem(LinkList L, int i, ElemType *e) { LinkList p = L->next; int j = 1; while (p && j < i) { p = p->next; ++j; } if (!p || j > i) { return ERROR; } *e = p->data; return OK; } /** * 初始条件:线性表 L 存在 * 操作结果:返回 L 中第一个值与元素 e 相同的元素在 L 中的位置。若元素不存在,则返回 0 * @param L * @param e * @param compare * @return */ int LocateElem(LinkList L, ElemType e, Status(*compare)(ElemType, ElemType)) { int i = 0; LinkList p = L->next; while (p) { i++; if (compare(p->data, e)) { return i; } p = p->next; } return 0; } Status compare(ElemType e1, ElemType e2) { if (e1 == e2) { return 1; } else { return 0; } } /** * 初始条件:线性表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是第一个,则用 pre_e 返回其前驱,否则失败,pre_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status PriorElem(LinkList L, ElemType cur_e, ElemType *pre_e) { LinkList q, p = L->next; while (p->next){ q = p->next; if (q->data == cur_e) { *pre_e = p->data; return OK; } p = q; } return INFEASIBLE; } /** * 初始条件:线性表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是最后一个,则用 next_e 返回其后驱,否则失败,next_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status NextElem(LinkList L, ElemType cur_e, ElemType *next_e) { LinkList q, p = L->next; while (p->next) { if (p->data == cur_e) { *next_e = p->next->data; return OK; } p = p->next; } return INFEASIBLE; } /** * 初始条件:线性表 L 存在,且 1 <= i <= ListLength(L) + 1 * 操作结果:在 L 中第 i 个元素前插入新的元素 e,L 的长度加 1 * @param L * @param i * @param e * @return */ Status ListInsert(LinkList L, int i, ElemType e) { int j = 0; LinkList p = L, s; while (p && j < i - 1) { p = p->next; ++j; } if (!p || j > i - 1) { return ERROR; } s = (LinkList)malloc(sizeof(struct LNode)); s->data = e; s->next = p->next; p->next = s; return OK; } /** * 初始条件:线性表 L 存在且非空,且 1 <= i <= ListLength(L) * 操作结果:删除 L 中的第 i 个元素并用 e 返回其值,L 的长度减 1 * @param S * @param i * @param e * @return */ Status ListDelete(LinkList L, int i, ElemType *e) { int j = 0; LinkList q, p = L; while (p->next && j < i - 1) { p = p->next; ++j; } if (!p || j > i - 1) { return ERROR; } *e = p->next->data; q = p->next; p->next = q->next; free(q); return OK; } /** * 初始条件:线性表 L 存在 * 操作结果:对线性表进行遍历,在遍历过程中对每个结点访问一次,遍历过程中调用 vi() 操作元素 * @param L * @param vi */ void TraverseList(LinkList L, void(*vi)(ElemType)) { LinkList p = L->next; while (p) { vi(p->data); p = p->next; } printf("\n"); } void vi(ElemType e) { printf("%d ", e); } /** * 操纵结果:前插法创建含 n 个元素的单链表 * @param L * @param n */ void CreateList_H(LinkList *L, int n) { InitList(L); LinkList p; for (int i = 0; i < n; ++i) { p = (LinkList)malloc(sizeof(struct LNode)); scanf("%d",&p->data); p->next = (*L)->next; (*L)->next = p; } } /** * 操纵结果:后插法创建含 n 个元素的单链表 * @param L * @param n */ void CreateList_R(LinkList *L, int n) { InitList(L); LinkList p, r = *L; for (int i = 0; i < n; ++i) { p = (LinkList)malloc(sizeof(struct LNode)); scanf("%d", &p->data); p->next = NULL; r->next = p; r = p; } } /*--------------------主函数------------------------*/ /** * 测试程序 * @return */ int main() { // 测试程序只测试函数是否有逻辑错误 LinkList list; int temp; ElemType *e; // CreateList_H(&list, 3); CreateList_R(&list, 3); printf("%d\n", ListEmpty(list)); printf("%d\n", ListLength(list)); TraverseList(list, vi); temp = ListInsert(list, 1, 99); TraverseList(list, vi); temp = ListInsert(list, 5, 100); TraverseList(list, vi); temp = GetElem(list, 3, e); printf("%d\n", *e); temp = PriorElem(list, 4, e); printf("%d\n", *e); temp = NextElem(list, 6, e); printf("%d\n", *e); printf("%d\n", LocateElem(list, 6, compare)); temp = ListDelete(list, 4, e); TraverseList(list, vi); ClearList(list); printf("%d\n", ListLength(list)); DestroyList(&list); }
---------> 引用自简书
考点在Code里面。

#include <stdio.h> #include <stdlib.h> #include "1.h" /************************************************************************ *这个结构体里定义的是链表头的信息,我们的链表操作和链表遍历都离不开链表头 ************************************************************************/ typedef struct student { DLinkListNode header; DLinkListNode *slider; //游标 int length; }TDLinkList; /*********************************************************************************************** *函数名: DLinkList_Create *参数:void *返回值:DLinkList*类型,是一个void*类型,然后再由接收函数进行强制类型转换 *功能:创建链表,并返回链表头 ***********************************************************************************************/ DLinkList* DLinkList_Create() { /* 为链表头获得空间,链表中其他数据节点的空间是在主函数中定义的,也就是插入链表时候由 结构体进行定义。 */ TDLinkList* ret = (TDLinkList*)malloc(sizeof (TDLinkList)); if (ret != NULL) { ret->length = 0; ret->slider = NULL; ret->header.next = NULL; ret->header.pre = NULL; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Destroy *参数:DLinkList* list 传进来的是链表头 *返回值:void *功能:销毁链表头 ***********************************************************************************************/ void DLinkList_Destroy(DLinkList* list) { free(list); } /*********************************************************************************************** *函数名: DLinkList_Clear *参数:DLinkList* list 传进来的是链表头 *返回值:void *功能:清空链表,并把链表头信息清空 ***********************************************************************************************/ void DLinkList_Clear(DLinkList* list) { TDLinkList *slist = (TDLinkList*)list; if (slist != NULL) { slist->length = 0; slist->header.next = NULL; slist->header.pre = NULL; slist->slider = NULL; } } /*********************************************************************************************** *函数名: DLinkList_Length *参数:DLinkList* list 传进来的是链表头 *返回值:int类型的整数 *功能:获得链表长度,并将链表的长度返回 ***********************************************************************************************/ int DLinkList_Length(DLinkList* list) { /*首先给返回值赋初值,如果函数的返回值为-1,则证明链表并不存在*/ int ret = -1; TDLinkList *slist = (TDLinkList*)list; if (slist != NULL) { ret = slist->length; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Insert *参数:DLinkList* list 传进来的是链表头 DLinkListNode* node 要插入的数据节点,其实是我们 *实际要插入的数据节点的指针 int pos 要插入链表中的位置(注意这个是从0开始算起的) *返回值:int类型的整数 *功能:如果插入元素成功返回1,否则返回其他。 ***********************************************************************************************/ int DLinkList_Insert(DLinkList* list, DLinkListNode* node, int pos) { TDLinkList *slist = (TDLinkList*)list; int ret = (slist != NULL); ret = ret && (pos >= 0); ret = ret && (node != NULL); int i = 0; if (ret) { DLinkListNode*current = (DLinkListNode*)slist; DLinkListNode*next = NULL; for (i = 0; (i < pos) && (current->next != NULL); i++) { current = current->next; } next = current->next; current->next = node; node->next = next; if (next != NULL) { // node->next = next; next->pre = node; } node->pre = current; if (current == (DLinkListNode*)slist) { node->pre = NULL; } if (slist->length == 0) { slist->slider = node; } slist->length++; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Get *参数:DLinkList* list 传进来的是链表头 int pos 要插入链表中的位置(注意这个是从0开始算起的) *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的链表指针和位置,可以获得这个位置上的数据节点信息。 ***********************************************************************************************/ DLinkListNode* DLinkList_Get(DLinkList* list, int pos) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode* ret = NULL; int i = 0; if ((slist != NULL)&& (pos >= 0) && (pos < slist->length)) { DLinkListNode*current = (DLinkListNode*)slist; //DLinkListNode*next = NULL; for (i = 0; i < pos; i++) { current = current->next; } /*current永远都是我们要找的节点的前一个节点*/ ret = current->next; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Delete *参数:DLinkList* list 传进来的是链表头 int pos 要插入链表中的位置(注意这个是从0开始算起的) *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的链表指针和位置,可以获取删除指定位置上的元素,并对指定位置上的元素进行删除。 ***********************************************************************************************/ DLinkListNode* DLinkList_Delete(DLinkList* list, int pos) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode * ret = NULL; int i = 0; if ((slist != NULL) && (pos >=0) && (pos < slist->length)) { DLinkListNode* current = (DLinkListNode*)(slist); DLinkListNode*next = NULL; for (i = 0; i < pos; i++) { current = current->next; } ret = current->next; next->pre = current;*/ next = ret->next; current->next = next; if (next != NULL) { next->pre = current; if (current == (DLinkListNode*)slist) { current->next = NULL; next->pre = NULL; } } if (slist->slider == ret) { slist->slider = next; } slist->length--; } return ret; } /*********************************************************************************************** *函数名: DLinkList_DeleteNode *参数:DLinkList* list 传进来的是链表头 int pos 要插入链表中的位置(注意这个是从0开始算起的) *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的链表指针和位置,通过游标指向我们要删除的元素,然后调用DLinkList_Delete函数 进行删除。 ***********************************************************************************************/ DLinkListNode* DLinkList_DeleteNode(DLinkList* list, DLinkListNode* node) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode * ret = NULL; int i = 0; if (slist != NULL) { DLinkListNode* current = (DLinkListNode*)(slist); for (i = 0; i < slist->length; i++) { if (current->next == node) { ret = current->next; break; } current = current->next; } if (current != NULL) { DLinkList_Delete (list, i); } } return ret; } /*********************************************************************************************** *函数名: DLinkList_Reset *参数:DLinkList* list 传进来的是链表头 *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的链表指针将游标重新指向头结点所指向的下一个元素的位置,也就是所谓的游标复位。 进行删除。 ***********************************************************************************************/ DLinkListNode* DLinkList_Reset(DLinkList* list) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode* ret = NULL; if (slist != NULL) { slist->slider = slist->header.next; ret = slist->slider; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Current *参数:DLinkList* list 传进来的是链表头 *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的指针,找到游标当前指向的元素,并将这个当前元素返回。 ***********************************************************************************************/ DLinkListNode* DLinkList_Current(DLinkList* list) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode* ret = NULL; if (slist != NULL) { ret = slist->slider; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Next *参数:DLinkList* list 传进来的是链表头 *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的指针,找到游标指向前一个元素,并将这个前一个元素返回。 ***********************************************************************************************/ DLinkListNode* DLinkList_Next(DLinkList* list) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode* ret = NULL; if( (slist != NULL) && (slist->slider != NULL) ) { ret = slist->slider; slist->slider = ret->next; } return ret; } /*********************************************************************************************** *函数名: DLinkList_Pre *参数:DLinkList* list 传进来的是链表头 *返回值:DLinkListNode*类型 也就是返回的是一个链表的节点结构体指针 *功能:通过传进来的指针,找到游标指向前一个元素,并将这个前一个元素返回。 ***********************************************************************************************/ DLinkListNode* DLinkList_Pre(DLinkList* list) { TDLinkList* slist = (TDLinkList*)list; DLinkListNode* ret = NULL; if (slist != NULL && slist->slider != NULL) { slist->slider = slist->slider->pre; ret = slist->slider; } return ret; }

#include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int ElemType; typedef struct LNode { ElemType data; struct LNode *next; }LNode, *LinkList; /** * 操作结果:构造一个空的线性表L * @param L */ void InitList(LinkList *L) { *L = (LinkList)malloc(sizeof(struct LNode)); if (!*L) { exit(OVERFLOW); } (*L)->next = *L; } /** * 初始条件:线性表 L存在 * 操作结果:销毁线性表 L * @param L */ void DestroyList(LinkList *L) { LinkList q, p = (*L)->next; while (p != *L) { q = p->next; free(p); p = q; } free(*L); *L = NULL; } /** * 初始条件:线性表 L 存在 * 操作结果:将 L 置为空表 * @param L */ void ClearList(LinkList *L) { LinkList p, q; *L = (*L)->next; p = (*L)->next; while (p != *L) { q = p->next; free(p); p = q; } (*L)->next = *L; } /** * 初始条件:线性表 L 存在 * 操作结果:若 L 为空表,返回 TRUE,否则返回 FALSE * @param L * @return */ Status ListEmpty(LinkList L) { if (L->next == L) { return TRUE; } else { return FALSE; } } /** * 初始条件:线性表 L 存在 * 操作结果:返回 L 中的数据元素个数 * @param L * @return */ int ListLength(LinkList L) { int i = 0; LinkList p = L->next; while (p != L) { i++; p = p->next; } return i; } /** * 初始条件:线性表 L 存在,且 1 <= i <= ListLength(L) * 操作结果:用 e 返回 L 中第 i 个元素的值 * @param L * @param i * @param e * @return */ Status GetElem(LinkList L, int i, ElemType *e) { LinkList p = L->next->next; int j = 1; if (i < 0 || i > ListLength(L)) { return ERROR; } while (j < i) { p = p->next; ++j; } *e = p->data; return OK; } /** * 初始条件:线性表 L 存在 * 操作结果:返回 L 中第一个值与元素 e 相同的元素在 L 中的位置。若元素不存在,则返回 0 * @param L * @param e * @param compare * @return */ int LocateElem(LinkList L, ElemType e, Status(*compare)(ElemType, ElemType)) { int i = 0; LinkList p = L->next->next; while (p != L->next) { i++; if (compare(p->data, e)) { return i; } p = p->next; } return 0; } Status compare(ElemType e1, ElemType e2) { if (e1 == e2) { return 1; } else { return 0; } } /** * 初始条件:线性表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是第一个,则用 pre_e 返回其前驱,否则失败,pre_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status PriorElem(LinkList L, ElemType cur_e, ElemType *pre_e) { LinkList q, p = L->next->next; q = p->next; while (q != L->next) { if (q->data == cur_e) { *pre_e = p->data; return OK; } p = q; q = q->next; } return INFEASIBLE; } /** * 初始条件:线性表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是最后一个,则用 next_e 返回其后驱,否则失败,next_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status NextElem(LinkList L, ElemType cur_e, ElemType *next_e) { LinkList p = L->next->next; while (p != L) { if (p->data == cur_e) { *next_e = p->next->data; return OK; } p = p->next; } return INFEASIBLE; } /** * 初始条件:线性表 L 存在,且 1 <= i <= ListLength(L) + 1 * 操作结果:在 L 中第 i 个元素前插入新的元素 e,L 的长度加 1 * @param L * @param i * @param e * @return */ Status ListInsert(LinkList *L, int i, ElemType e) { int j = 0; LinkList p = *L, s; if (i <= 0 || i > ListLength(*L) + 1) { return ERROR; } while (j < i - 1) { p = p->next; j++; } s = (LinkList)malloc(sizeof(struct LNode)); s->data = e; s->next = p->next; p->next = s; return OK; } /** * 初始条件:线性表 L 存在且非空,且 1 <= i <= ListLength(L) * 操作结果:删除 L 中的第 i 个元素并用 e 返回其值,L 的长度减 1 * @param S * @param i * @param e * @return */ Status ListDelete(LinkList *L, int i, ElemType *e) { int j = 0; LinkList q, p = (*L)->next; if (i < 0 || i > ListLength(*L)) { return ERROR; } while (j < i - 1) { p = p->next; ++j; } *e = p->next->data; q = p->next; p->next = q->next; free(q); return OK; } /** * 初始条件:线性表 L 存在 * 操作结果:对线性表进行遍历,在遍历过程中对每个结点访问一次,遍历过程中调用 vi() 操作元素 * @param L * @param vi */ void TraverseList(LinkList L, void(*vi)(ElemType)) { LinkList p = L->next; while (p != L) { vi(p->data); p = p->next; } printf("\n"); } void vi(ElemType e) { printf("%d ", e); } /** * 操纵结果:前插法创建含 n 个元素的单链表 * @param L * @param n */ void CreateList_H(LinkList *L, int n) { InitList(L); LinkList p; for (int i = 0; i < n; ++i) { p = (LinkList)malloc(sizeof(struct LNode)); scanf("%d",&p->data); p->next = (*L)->next; (*L)->next = p; } } /** * 操纵结果:后插法创建含 n 个元素的单链表 * @param L * @param n */ void CreateList_R(LinkList *L, int n) { InitList(L); LinkList p, r = (*L)->next; for (int i = 0; i < n; ++i) { p = (LinkList)malloc(sizeof(struct LNode)); if (!p) { exit(OVERFLOW); } scanf("%d", &p->data); p->next = *L; r->next = p; r = p; } } /*--------------------主函数------------------------*/ /** * 测试程序 * @return */ int main() { // 测试程序只测试函数是否有逻辑错误 LinkList list; int temp; ElemType *e; CreateList_H(&list, 3); // CreateList_R(&list, 3); printf("%d\n", ListEmpty(list)); printf("%d\n", ListLength(list)); TraverseList(list, vi); temp = ListInsert(&list, 1, 99); TraverseList(list, vi); temp = ListInsert(&list, 5, 100); TraverseList(list, vi); temp = GetElem(list, 3, e); printf("%d\n", *e); temp = PriorElem(list, 4, e); printf("%d\n", *e); temp = NextElem(list, 6, e); printf("%d\n", *e); printf("%d\n", LocateElem(list, 6, compare)); temp = ListDelete(&list, 4, e); TraverseList(list, vi); ClearList(&list); printf("%d\n", ListLength(list)); DestroyList(&list); }

#include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int ElemType; typedef struct DuLNode { ElemType data; struct DuLNode *prior; struct DuLNode *next; }DuLNode, *DuLinkList; /** * 操作结果:构造一个空的双向链表 L * @param L */ void InitList(DuLinkList *L) { *L = (DuLinkList)malloc(sizeof(struct DuLNode)); if (*L) { (*L)->next = (*L)->prior = *L; } else { exit(OVERFLOW); } } /** * 初始条件:双向链表 L存在 * 操作结果:销毁双向链表 L * @param L */ void DestroyList(DuLinkList *L) { DuLinkList q, p = (*L)->next; //p 指向第一个节点 while (p != *L) { q = p->next; free(p); p = q; } free(*L); *L = NULL; } /** * 初始条件:双向链表 L 存在 * 操作结果:将 L 置空 * @param L */ void ClearList(DuLinkList L) { DuLinkList q, p = L->next; //p 指向第一个节点 while (p != L) { //p 没有到表头 q = p->next; free(p); p = q; } L->next = L->prior = L; //头节点两个指针均指向本身 } /** * 初始条件:双向链表 L 存在 * 操作结果:若 L 为空表,返回 TRUE,否则返回 FALSE * @param L * @return */ Status ListEmpty(DuLinkList L) { if (L->next == L && L->prior == L) { return TRUE; } else { return FALSE; } } /** * 初始条件:双向链表表 L 存在 * 操作结果:返回 L 中的数据元素个数 * @param L * @return */ int ListLength(DuLinkList L) { int i = 0; DuLinkList p = L->next; //p 指向第一个节点 while (p != L) { //p 没有到表头 i++; p = p->next; } return i; } /** * 初始条件:双向链表表 L 存在,且 1 <= i <= ListLength(L) * 操作结果:用 e 返回 L 中第 i 个元素的值 * @param L * @param i * @param e * @return */ Status GetElem(DuLinkList L, int i, ElemType *e) { DuLinkList p = L->next; //p 指向第一个节点 int j = 1; //计数器 while (p != L && j < i) { //顺指针向后查询,直到 p 指向第 i 个元素或 p 指向头结点 p = p->next; ++j; } if (p == L || j > i) { //第 i 个元素不存在 return ERROR; } *e = p->data; //取得第 i 个元素 return OK; } /** * 初始条件:双向链表 L 存在 * 操作结果:返回 L 中第一个值与元素 e 相同的元素在 L 中的位置。若元素不存在,则返回 0 * @param L * @param e * @param compare * @return */ int LocateElem(DuLinkList L, ElemType e, Status(*compare)(ElemType, ElemType)) { int i = 0; DuLinkList p = L->next; //p 指向第一个节点 while (p != L) { //p 没有到表头 i++; if (compare(p->data, e)) { //找到该元素 return i; } p = p->next; } return 0; } Status compare(ElemType e1, ElemType e2) { if (e1 == e2) { return 1; } else { return 0; } } /** * 初始条件:双向链表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是第一个,则用 pre_e 返回其前驱,否则失败,pre_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status PriorElem(DuLinkList L, ElemType cur_e, ElemType *pre_e) { DuLinkList p = L->next->next; //p 指向第二个元素 while (p != L) { if (p->data == cur_e) { *pre_e = p->prior->data; //返回前驱 return OK; } p = p->next; } return INFEASIBLE; } /** * 初始条件:双向链表表 L 存在 * 操作结果:若 cur_e 是 L 中的元素,且不是最后一个,则用 next_e 返回其后驱,否则失败,next_e 无定义 * @param L * @param cur_e * @param pre_e * @return */ Status NextElem(DuLinkList L, ElemType cur_e, ElemType *next_e) { DuLinkList p = L->next->next; //p 指向第二个元素 while (p != L) { if (p->prior->data == cur_e) { *next_e = p->data; //返回后驱 return OK; } p = p->next; } return INFEASIBLE; } /** * 返回 L 中第 i 个元素的地址,若 i = 0 返回头结点,若 i 不存在,返回 NULL * @param L * @param i * @return */ DuLinkList GetElemP(DuLinkList L, int i) { DuLinkList p = L; //p 指向头结点 if (i < 0 || i > ListLength(L)) { //i 值不合法 return NULL; } for (int j = 1; j <= i; j++) { p = p->next; } return p; } /** * 初始条件:双向链表 L 存在,且 1 <= i <= ListLength(L) + 1 * 操作结果:在 L 中第 i 个元素前插入新的元素 e,L 的长度加 1 * @param L * @param i * @param e * @return */ Status ListInsert(DuLinkList L, int i, ElemType e) { DuLinkList p, s; if (i < 1 || i > (ListLength(L) + 1)) { //i 值不合法 return ERROR; } p = GetElemP(L, i - 1); if (!p) { //在 L 中确定第 i 个元素的前驱位置指针 p return ERROR; // p = NULL 时,第 i 个元素不存在 } s = (DuLinkList)malloc(sizeof(struct DuLNode)); if (!s) { exit(OVERFLOW); } s->data = e; s->prior = p; //在 i - 1 个元素后插入 s->next = p->next; p->next->prior = s; p->next = s; return OK; } /** * 初始条件:双向链表 L 存在且非空,且 1 <= i <= ListLength(L) * 操作结果:删除 L 中的第 i 个元素并用 e 返回其值,L 的长度减 1 * @param S * @param i * @param e * @return */ Status ListDelete(DuLinkList L, int i, ElemType *e) { DuLinkList p; p = GetElemP(L, i); if (!p) { //在 L 中确定第 i 个元素的位置指针 p return ERROR; //p = NULL 是,第 i 个元素不存在,也就是 i 值不合法 } *e = p->data; p->prior->next = p->next; //修改被删除结点的前驱结点的后继指针 p->next->prior = p->prior; //修改被删除结点的后继结点的前驱指针 free(p); return OK; } /** * 初始条件:双向链表 L 存在 * 操作结果:由头结点出发,对链表进行遍历,在遍历过程中对每个结点访问一次,遍历过程中调用 vi() 操作元素 * @param L * @param vi */ void TraverseList(DuLinkList L, void(*vi)(ElemType)) { DuLinkList p = L->next; //p 指向第一个元素 while (p != L) { //遍历 vi(p->data); p = p->next; } printf("\n"); } void vi(ElemType e) { printf("%d ", e); } /** * 操纵结果:前插法创建含 n 个元素的双向链表 * @param L * @param n */ void CreateList_H(DuLinkList *L, int n) { InitList(L); DuLinkList p; for (int i = 0; i < n; ++i) { p = (DuLinkList)malloc(sizeof(struct DuLNode)); if (!p) { exit(OVERFLOW); } scanf("%d",&p->data); p->prior = *L; p->next = (*L)->next; (*L)->next->prior = p; (*L)->next = p; } } /** * 操纵结果:后插法创建含 n 个元素的单链表 * @param L * @param n */ void CreateList_R(DuLinkList *L, int n) { InitList(L); DuLinkList p, r = (*L)->next; for (int i = 0; i < n; ++i) { p = (DuLinkList)malloc(sizeof(struct DuLNode)); if (!p) { exit(OVERFLOW); } scanf("%d", &p->data); p->prior = r; p->next = *L; r->next->prior = p; r->next = p; r = p; } } /*--------------------主函数------------------------*/ /** * 测试程序 * @return */ int main() { // 测试程序只测试函数是否有逻辑错误 DuLinkList list; int temp; ElemType *e; // CreateList_H(&list, 3); CreateList_R(&list, 3); printf("%d\n", ListEmpty(list)); printf("%d\n", ListLength(list)); TraverseList(list, vi); temp = ListInsert(list, 1, 99); TraverseList(list, vi); temp = ListInsert(list, 5, 100); TraverseList(list, vi); temp = GetElem(list, 3, e); printf("%d\n", *e); temp = PriorElem(list, 5, e); printf("%d\n", *e); temp = NextElem(list, 5, e); printf("%d\n", *e); printf("%d\n", LocateElem(list, 6, compare)); temp = ListDelete(list, 4, e); TraverseList(list, vi); ClearList(list); printf("%d\n", ListLength(list)); DestroyList(&list); }

#include <bits/stdc++.h> using namespace std; #define Stack_size 10010 #define Stack_Rise 100 typedef struct { int *base; int *top; int roomstack;//栈的容量 }Stack; bool InitStack(Stack &S) { S.base = (int *)malloc(Stack_size*sizeof(int)); if(S.base==NULL)//if(!S.base) return false; S.top = S.base; S.roomstack+=Stack_size; return true; } int GetTop(Stack &S) { if(S.top==S.base) return -1; // 栈空 , 返回 -1 return *(S.top-1); } bool Push(Stack &S,int e) { if(S.top-S.base>=S.roomstack) // 空间不足 , 继续分配 S.base = (int *)realloc(S.base,(S.roomstack+Stack_Rise)*sizeof(int)); if(!S.base) return false; S.top = S.base+S.roomstack; S.roomstack+=Stack_Rise; *S.top++ = e; return true; } int Pop(Stack &S) { if(S.base==S.top) return -1; else return *(--S.top); } int main() { Stack Sta; InitStack(Sta); int n; scanf("%d",&n); int t; while(n--) { scanf("%d",&t); Push(Sta,t); } printf("%d\n",GetTop(Sta)); }

#include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int SElemType; typedef struct StackNode { SElemType data; //数据域 struct StackNode *next; //指针域 }StackNode, *LinkStack; Status InitStack(LinkStack *S); Status DestroyStack(LinkStack *S); Status ClearStack(LinkStack *S); Status StackEmpty(LinkStack S); int StackLength(LinkStack S); Status GetTop(LinkStack S, SElemType *e); Status Push(LinkStack *S, SElemType e); Status Pop(LinkStack *S, SElemType *e); void StackTraverse(LinkStack S, void(*vi)(SElemType)); /** * 操作结果:构造一个空栈 S * @param L * @return */ Status InitStack(LinkStack *S) { S = NULL; //构造一个空栈,栈顶指针置空 return OK; } /** * 初始条件:栈 S 存在 * 操作结果:栈 S 被销毁 * @param S * @return */ Status DestroyStack(LinkStack *S) { LinkStack p; while (*S) { //未到栈底 p = (*S)->next; free(*S); //释放栈顶空间 *S = p; } return OK; } /** * 初始条件:栈 S 存在 * 操作结果:将栈 S 清空 * @param S */ Status ClearStack(LinkStack *S) { LinkStack q, p = (*S)->next; // p 指向栈顶元素 while (p) { //未到栈底 q = p->next; free(p); p = q; } (*S) = NULL; return OK; } /** * 初始条件:栈 S 存在 * 操作结果:若 S 是空栈,返回 true,否则返回 false * @param S * @return */ Status StackEmpty(LinkStack S) { if (S == NULL) { return TRUE; } else { return FALSE; } } /** * 初始条件:栈 S 存在 * 操作结果:返回栈 S 长度 * @param S * @return */ int StackLength(LinkStack S) { int i = 0; //计数器 LinkStack p = S; //p指向栈顶元素 while (p) { //未到栈底 i++; p = p->next; } return i; } /** * 初始条件:栈 S 存在且非空 * 操作结果;用 e 返回栈 S 的栈顶元素,不修改栈顶指针 * @param S * @return */ Status GetTop(LinkStack S, SElemType *e) { if (S) { //S 非空 *e = S->data; return OK; } return ERROR; } /** * 初始条件:栈 S 存在 * 操作结果:插入元素 e 为新的栈顶元素 * @param L * @param e * @return */ Status Push(LinkStack *S, SElemType e) { LinkStack p; p = (LinkStack)malloc(sizeof(struct StackNode)); //生成新结点 p->data = e; p->next = *S; //将新结点插入栈顶 *S = p; //修改栈顶指针 return OK; } /** * 初始条件:栈 S 存在且非空 * 操作结果:删除栈顶元素,并用 e 返回且值 * @param S * @param e * @return */ Status Pop(LinkStack *S, SElemType *e) { LinkStack p; if (!S) { return ERROR; } *e = (*S)->data; //返回栈顶元素 p = *S; //p 临时保存栈顶空间,以备释放 *S = (*S)->next; //修改栈顶指针 free(p); //释放原栈栈顶空间 return OK; } /** * 初始条件:栈 S 存在且非空 * 操作结果:从栈底到栈顶依次对 S 中的每个元素进行访问 * @param S * @param vi */ void StackTraverse(LinkStack S, void(*vi)(SElemType)) { LinkStack p = S; //p 指向栈顶 while (p) { vi(p->data); p = p->next; } printf("\n"); } void vi(SElemType e) { printf("%d ", e); } /** * 主函数,测试程序 * @return */ int main() { LinkStack s = NULL; SElemType e; InitStack(&s); printf("栈的长度:%d\n", StackLength(s)); printf("栈是否为空:%d\n", StackEmpty(s)); Push(&s, 3); Push(&s, 4); Push(&s, 5); Push(&s, 6); StackTraverse(s,vi); printf("栈的长度:%d\n", StackLength(s)); printf("栈是否为空:%d\n", StackEmpty(s)); GetTop(s, &e); printf("栈顶元素:%d\n", e); printf("栈的长度:%d\n", StackLength(s)); Pop(&s, &e); StackTraverse(s, vi); ClearStack(&s); printf("栈的长度:%d\n", StackLength(s)); printf("栈是否为空:%d\n", StackEmpty(s)); DestroyStack(&s); }

#include <stdio.h> #include <stdlib.h> #define MAX_QUEUE_SIZE 100 #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int QElemType; typedef struct { QElemType *base; //存储空间基地址 int front; //头指针 int rear; //尾指针 int QueueSize; //队列容量 }SqQueue; Status InitQueue(SqQueue *); Status DestroyQueue(SqQueue *); Status ClearQueue(SqQueue *); Status QueueEmpty(SqQueue ); int QueueLength(SqQueue); Status GetHead(SqQueue, QElemType *); Status EnQueue(SqQueue *, QElemType); Status DeQueue(SqQueue *, QElemType *); void QueueTraverse(SqQueue , void(*vi)(QElemType)); /** * 操作结果:构造一个空队列 Q * @param e * @return */ Status InitQueue(SqQueue *Q) { Q->base = (QElemType *)malloc(MAX_QUEUE_SIZE * sizeof(SqQueue)); if (!Q->base) { exit(OVERFLOW); } Q->front = Q->rear = 0; //头指针尾指针置为零,队列为空 return OK; } /** * 初始条件:队列 Q 存在 * 操作结果:队列 Q 被销毁 * @param Q * @return */ Status DestroyQueue(SqQueue *Q) { if (Q->base) { free(Q->base); } Q->base = NULL; Q->front = Q->rear = 0; } /** * 初始条件:队列 Q 存在 * 操作结果:清空队列 Q * @param Q * @return */ Status ClearQueue(SqQueue *Q) { Q->front = Q->rear = 0; } /** * 初始条件:队列 Q 存在 * 操作结果:若 Q 为空队列,则返回 true,否则返回 false * @param Q * @return */ Status QueueEmpty(SqQueue Q) { if (Q.front == Q.rear) { return TRUE; } else { return FALSE; } } /** * 初始条件:队列 Q 存在 * 操作结果:返回 Q 中元素个数,即队列长度 * @param Q * @return */ int QueueLength(SqQueue Q) { return (Q.rear - Q.front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:返回 Q 中队头元素 * @param Q * @param e * @return */ Status GetHead(SqQueue Q, QElemType *e) { if (Q.front == Q.rear) { return ERROR; } *e = Q.base[Q.front]; return OK; } /** * 初始条件:队列 Q 存在 * 操作结果:插入入元素 e 为 Q 的新队尾元素 * @param Q * @param e * @return */ Status EnQueue(SqQueue *Q, QElemType e) { if ((Q->rear + 1) % MAX_QUEUE_SIZE == Q->front) { return ERROR; //队尾指针在循环意义上加 1 后等于头指针,表示队满 } Q->base[Q->rear] = e; Q->rear = (Q->rear + 1) % MAX_QUEUE_SIZE; //队尾指针加 1 return OK; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:删除 Q 的队头元素,且用 e 返回 * @param Q * @param e * @return */ Status DeQueue(SqQueue *Q, QElemType *e) { if (Q->front == Q->rear) { return ERROR; } *e = Q->base[Q->front]; Q->front = (Q->front + 1) % MAX_QUEUE_SIZE; //队头指针加 1 return OK; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:从队头到队尾,依次对遍历队列中每个元素 * @param Q * @param vi */ void QueueTraverse(SqQueue Q, void(*vi)(QElemType)) { int i = Q.front; while (i != Q.rear) { vi(Q.base[i]); //遍历 i = (i + 1) % MAX_QUEUE_SIZE; } printf("\n"); } /** * 遍历函数 * @param e */ void vi(QElemType e) { printf("%d ",e); } /** * 主函数,测试程序 * @return */ int main() { SqQueue q; QElemType e; InitQueue(&q); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); EnQueue(&q, 3); EnQueue(&q, 4); EnQueue(&q, 5); EnQueue(&q, 6); QueueTraverse(q, vi); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); GetHead(q, &e); printf("队列的头元素:%d\n", e); DeQueue(&q, &e); QueueTraverse(q, vi); ClearQueue(&q); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); DestroyQueue(&q); }

#include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -1 #define INFEASIBLE 0 typedef int Status; typedef int QElemType; typedef struct QNode { QElemType data; struct QNode *next; }QNode, *QueuePtr; typedef struct { QueuePtr front; //队头指针 QueuePtr rear; //队尾指针 }LinkQueue; Status InitQueue(LinkQueue *); Status DestroyQueue(LinkQueue *); Status ClearQueue(LinkQueue *); Status QueueEmpty(LinkQueue ); int QueueLength(LinkQueue); Status GetHead(LinkQueue, QElemType *); Status EnQueue(LinkQueue *, QElemType); Status DeQueue(LinkQueue *, QElemType *); void QueueTraverse(LinkQueue , void(*vi)(QElemType)); /** * 操作结果:构造一个空队列 Q * @param Q * @return */ Status InitQueue(LinkQueue *Q) { if (!(Q->front = Q->rear = (QueuePtr)malloc(sizeof(struct QNode)))) { exit(OVERFLOW); } Q->front->next = NULL; return OK; } /** * 初始条件:队列 Q 存在 * 操作结果:队列 Q 被销毁 * @param Q * @return */ Status DestroyQueue(LinkQueue *Q) { while (Q->front) { //指向队尾时结束循环 Q->rear = Q->front->next; // 队尾指针指向队头指针的下一个结点 free(Q->front); //释放队头结点 Q->front = Q->rear; //修改队头指针 } return OK; } /** * 初始条件:队列 Q 存在 * 操作结果:清空队列 Q * @param Q * @return */ Status ClearQueue(LinkQueue *Q) { QueuePtr p, q; Q->rear = Q->front; //队尾指针指向头结点 p = Q->front->next; //p 指向队列第一个元素 Q->front->next = NULL; //队头指针 next 域置空 while (p) { q = p->next; free(p); p = q; } return OK; } /** * 初始条件:队列 Q 存在 * 操作结果:若 Q 为空队列,则返回 true,否则返回 false * @param Q * @return */ Status QueueEmpty(LinkQueue Q) { if (Q.front->next == NULL) { return TRUE; } else { return FALSE; } } /** * 初始条件:队列 Q 存在 * 操作结果:返回 Q 中元素个数,即队列长度 * @param Q * @return */ int QueueLength(LinkQueue Q) { int i = 0; //计数器 QueuePtr p = Q.front->next; //p 指向队头元素 while (p) { i++; p = p->next; } return i; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:返回 Q 中队头元素 * @param Q * @param e * @return */ Status GetHead(LinkQueue Q, QElemType *e) { if (Q.front != Q.rear) { *e = Q.front->next->data; return OK; } return INFEASIBLE; } /** * 初始条件:队列 Q 存在 * 操作结果:插入入元素 e 为 Q 的新队尾元素 * @param Q * @param e * @return */ Status EnQueue(LinkQueue *Q, QElemType e) { QueuePtr p; p = (QueuePtr)malloc(sizeof(struct QNode)); //开辟新结点 p->data = e; p->next = NULL; Q->rear->next = p; //将新结点插入到队尾 Q->rear = p; //修改队尾指针 return OK; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:删除 Q 的队头元素,且用 e 返回 * @param Q * @param e * @return */ Status DeQueue(LinkQueue *Q, QElemType *e) { QueuePtr p; if (Q->front == Q->rear) { //判断是否为空队列 return ERROR; } p = Q->front->next; //p 指向队头元素 *e = p->data; Q->front->next = p->next; //修改头指针 if (Q->rear == p) { //如果删除的是队列最后一个元素 Q->rear = Q->front; //队尾指针指向头结点 } free(p); return OK; } /** * 初始条件:队列 Q 存在且非空 * 操作结果:从队头到队尾,依次对遍历队列中每个元素 * @param Q * @param vi */ void QueueTraverse(LinkQueue Q, void(*vi)(QElemType)) { QueuePtr p = Q.front->next; //p 指向队头元素 while (p) { vi(p->data); //遍历 p = p->next; } printf("\n"); } /** * 遍历函数 * @param e */ void vi(QElemType e) { printf("%d ",e); } /** * 主函数,测试程序 * @return */ int main() { LinkQueue q; QElemType e; InitQueue(&q); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); EnQueue(&q, 3); EnQueue(&q, 4); EnQueue(&q, 5); EnQueue(&q, 6); QueueTraverse(q, vi); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); GetHead(q, &e); printf("队列的头元素:%d\n", e); DeQueue(&q, &e); QueueTraverse(q, vi); ClearQueue(&q); printf("队列的长度:%d\n", QueueLength(q)); printf("队列是否为空:%d\n", QueueEmpty(q)); DestroyQueue(&q); }

#include<iostream> #include<stdio.h> #include<math.h> #define LEN sizeof(struct DQueuelist) using namespace std; typedef struct DQueuelist //定义结构体结点 { int data; //结构体数据域 struct DQueuelist *prior; //结构体前向指针 struct DQueuelist *next; //结构体后向指针 }DQueuelist, *DQueueptr; typedef struct //定义双端队列 { DQueueptr front; //头指针,指向链队列头结点 DQueueptr rear; //尾指针,指向链队列最后一个结点 }LinkDQueue; //函数声明部分 void Error(char *s); LinkDQueue Creat_DQueuelist(); //错误处理函数 void En_DQueuelist(LinkDQueue &q, int e); //创建双端队列函数 void De_DQueuelist(LinkDQueue &q, int e); //入队函数 void Print_DQueuelist(LinkDQueue &q); //出队函数 int Getlength_DQueuelist(LinkDQueue &q); //计算双端队列长度函数 void Gethead_DQueuelist(LinkDQueue &q, int e); //得到双端队列的端口处的元素 void Destroy_DQueuelist(LinkDQueue &q); //销毁双端队列函数 //函数定义定义 void Error(char *s) { cout << s << endl; exit(1); } LinkDQueue Creat_DQueuelist() //创建双端队列 { DQueuelist *pnew; //初始化双端队列 LinkDQueue head; head.front = head.rear = (struct DQueuelist *)malloc(LEN); //创建头结点 head.front->data = 0; head.front->next = NULL; head.rear->next = NULL; int length = 0; int number = 0; cout << "请输入双端队列长度:"; cin >> length; cout << "请输入双端队列数据:"; for (int i = 0; i < length; i++) //端口2创建双端队列 { pnew = (struct DQueuelist *)malloc(LEN); if (!pnew) Error("内存分配失败!"); cin >> number; pnew->data = number; pnew->next = NULL; head.rear->next = pnew; pnew->prior = head.rear; head.rear = pnew; } return head; } void En_DQueuelist(LinkDQueue &q, int e) //入队函数 {//1表示在端口1入队,2表示在端口2入队 int a; DQueuelist *ptr = NULL; DQueuelist *temp = NULL; cout << "请选择入队端口(默认端口为1和2):"; cin >> a; switch (a) { case 1: ptr = (struct DQueuelist *)malloc(LEN);//端口1入队只改变队头指针,不改变队尾指针, //且将结点插入到头结点之后,使其成为第一个结点 if (!ptr) Error("内存分配失败!"); ptr->data = e; temp = q.front->next; q.front->next = ptr; ptr->next = temp; temp->prior = ptr; ptr->prior = q.front; break; case 2: ptr = (struct DQueuelist *)malloc(LEN); //端口2入队只改变队尾指针,不改变队头指针 //将该结点直接插入到最后面即可 if (!ptr) Error("内存分配失败!"); ptr->data = e; ptr->next = NULL; q.rear->next = ptr; ptr->prior = q.rear; q.rear = ptr; break; } } void De_DQueuelist(LinkDQueue &q, int e) //出队函数 {//1表示在端口1出队,2表示在端口2出队 int a; cout << "请输入出队端口(默认端口为1和2):"; cin >> a; DQueuelist *ptr = NULL; DQueuelist *temp = NULL; switch (a) { case 1://端口1出队,将头结点后的第一个结点删除即可,改变头指针,不改变尾指针 if (q.front->next == NULL) Error("该队列为空!"); ptr = q.front->next; e = ptr->data; cout << "端口1出队的元素是:" << e << endl; q.front->next = ptr->next; ptr->next->prior = q.front; if (q.rear == ptr) q.rear = q.front; delete ptr; break; case 2://端口2出队,直接将最后一个结点删除即可,改变尾指针,不改变头指针 if (q.rear == NULL) Error("该队列为空!"); ptr = q.rear->prior; temp = q.rear; e = temp->data; cout << "端口2出队的元素是:" << e << endl; ptr->next = NULL; q.rear = ptr; if (q.front == ptr) q.front = q.rear; delete temp; break; } } void Print_DQueuelist(LinkDQueue &q) //输出函数 { int e = 0; int n = 0; cout << "请输入顺序出队端口:"; cin >> n; switch (n) { case 1: //端口1顺序输出,正向输出 while (q.front->next != NULL) { DQueuelist *p = NULL; p = q.front->next; e = p->data; cout << e << " "; q.front->next = p->next; //p->next->prior = q.rear; if (q.rear == p) q.rear = q.front; } cout << endl; break; case 2://端口2顺序输出,逆向输出 while ((q.rear != NULL)&&(q.rear->data!=0)) { DQueuelist *p = NULL; DQueuelist *temp = NULL; p = q.rear->prior; temp = q.rear; e = temp->data; cout << e << " "; p->next = NULL; q.rear = p; if (q.front == p) q.rear = q.front; } cout << endl; break; } } int Getlength_DQueuelist(LinkDQueue &q) //计算双端队列长度函数 { DQueuelist *p = NULL; p = q.front; int length = 0; while (p->next != NULL) { length++; p = p->next; } return length; } void Gethead_DQueuelist(LinkDQueue &q, int e) //得到双端队列的端口处的元素,并不修改指针头和尾,只是简单的输出而已 {//1表示得到双端队列端口1的元素,2表示得到双端队列断口2的元素 cout << "请输入出队端口:"; int a = 0; cin >> a; switch (a) { case 1: if (q.front->next == NULL) //判断头结点之后一个节点是否为空 Error("该队列为空!"); e = q.front->next->data; cout << "端口1的第一个元素是:" << e << endl; break; case 2: if (q.rear == NULL) //判断最后一个结点是否为空 Error("该队列为空!"); e = q.rear->data; cout << "端口2的第一个元素是:" << e << endl; break; } } void Destroy_DQueuelist(LinkDQueue &q) //销毁函数 { while (q.front) { q.rear = q.front->next; delete q.front; q.front = q.rear; } cout << "该链队列销毁成功!" << endl; } int main() { LinkDQueue Q; Q = Creat_DQueuelist(); cout << "该双端队列的长度是:" << Getlength_DQueuelist(Q) << endl; int m = 0; for (int i = 0; i < 2; i++) { int n = 0; cout << "请输入要入队的元素:"; cin >> n; En_DQueuelist(Q, n); } cout << "入队后双端队列的长度是:" << Getlength_DQueuelist(Q) << endl; for (int j = 0; j < 2; j++) { De_DQueuelist(Q, m); } cout << "出队后双端队列的长度是:" << Getlength_DQueuelist(Q) << endl; Print_DQueuelist(Q); Destroy_DQueuelist(Q); return 0; }

#include <iostream> typedef int KeyType; typedef struct { KeyType key; int info; }ElemType; typedef struct { ElemType *elem; // 数据元素存储空间基址,建表时 int length; // 表的长度 } SSTable; int Sq_search(SSTable ST, KeyType key) { // 在无序表中查找元素key,查找成功时,返回元素在表中的位置 ,否则返回0 int i=ST.length; while (i>=1&&ST.elem[i].key!=key) i--; return i; } int Init_search(SSTable &ST,int length)//初始化表 { ST.length=length; ST.elem = (ElemType *)malloc(sizeof(ElemType)*(length+1)); } int Creat_search(SSTable &ST,int length)//创建表 { ElemType *ptr = ST.elem; int temp =0; int i=0; ptr++; //我们将第一个元素空出来! while (temp!=-1&&(i++)<length) { scanf("%d",&temp); ptr++->key=temp; } } int main() { SSTable table; Init_search(table,5); Creat_search(table,5); printf("已经找到位置:%d",Sq_search(table, 13)); return 0; }
对于Hash,我们是怎样来处理冲突的。现在就来介绍一些经典的Hash冲突处理的方法。主要包括
( 1)开放地址法
(2)拉链法
(3)再哈希法
(4)建立公共溢出区
(1)开放地址法
基本思想:当发生地址冲突时,按照某种方法继续探测Hash表中其它存储单元,直到找到空位置为止。描述如下
其中
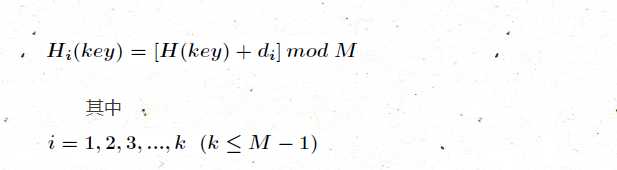
(2)拉链法
拉链法又叫链地址法,适合处理冲突比较严重的情况。基本思想是把所有关键字为同义词的记录存储在同一个
线性链表中。
(3)再哈希法
再哈希法又叫双哈希法,有多个不同的Hash函数,当发生冲突时,使用第二个,第三个,....,等哈希函数
计算地址,直到无冲突。虽然不易发生聚集,但是增加了计算时间。
(4)建立公共溢出区
建立公共溢出区的基本思想是:假设哈希函数的值域是[1,m-1],则设向量HashTable[0...m-1]为基本
表,每个分量存放一个记录,另外设向量OverTable[0...v]为溢出表,所有关键字和基本表中关键字为同义
词的记录,不管它们由哈希函数得到的哈希地址是什么,一旦发生冲突,都填入溢出表。

#include <iostream> #include <string.h> #include <stdio.h> using namespace std; const int N = 35; struct node { int key; //关键字 int len; //每个节点引出的链表长度 bool flag; //有数据的标志 node *next; }; node list[N]; void Init(node list[]) { for(int i=0; i<N; i++) { list[i].len = 0; list[i].flag = 0; list[i].next = NULL; } } void Insert(node list[], int val, int m) { int id = val % m; if(!list[id].flag) { list[id].key = val; list[id].flag = 1; } else { node *p = new node(); p->key = val; p->next = list[id].next; list[id].next = p; } } //输出HashTable void Print(node list[], int m) { for(int i=0; i<m; i++) { node *p = list[i].next; if(!list[i].flag) printf("The %dth record is NULL!\n", i); else { printf("The %dth record is %d", i, list[i].key); list[i].len++; while(p) { printf("->%d", p->key); p = p->next; list[i].len++; } puts(""); } } } //计算平均查找长度 double ASL(node list[], int m) { double ans = 0; for(int i=0; i<m; i++) ans += (list[i].len + 1) * list[i].len / 2.0; return ans / m; } int main() { int n, m; Init(list); scanf("%d %d", &n, &m); for(int i=0; i<n; i++) { int val; scanf("%d", &val); Insert(list, val, m); } Print(list, m); printf("The Average Search Length is %.5lf\n", ASL(list, m)); return 0; } /** 12 11 47 7 29 11 16 92 22 8 3 37 89 50 */

#include<stdio.h> /* EOF(=^Z或F6),NULL */ #include<stdlib.h> /* atoi() */ #include<io.h> /* eof() */ #include<math.h> /* floor(),ceil(),abs() */ //#include<process.h> /* exit() */ /* 函数结果状态代码 */ #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 /* #define OVERFLOW -2 因为在math.h中已定义OVERFLOW的值为3,故去掉此行 */ typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */ typedef int ElemType; #define MAX_ARRAY_DIM 8 /* 假设数组维数的最大值为8 */ typedef struct { ElemType *base; /* 数组元素基址,由InitArray分配 */ int dim; /* 数组维数 */ int *bounds; /* 数组维界基址,由InitArray分配 */ int *constants; /* 数组映象函数常量基址,由InitArray分配 */ } Array; Status InitArray(Array *A,int dim,...) { /* 若维数dim和各维长度合法,则构造相应的数组A,并返回OK */ int elemtotal=1,i; /* elemtotal是元素总值 */ va_list ap; if(dim<1||dim>MAX_ARRAY_DIM) return ERROR; (*A).dim=dim; (*A).bounds=(int *)malloc(dim*sizeof(int)); if(!(*A).bounds) exit(OVERFLOW); va_start(ap,dim); for(i=0; i<dim; ++i) { (*A).bounds[i]=va_arg(ap,int); if((*A).bounds[i]<0) return UNDERFLOW; /* 在math.h中定义为4 */ elemtotal*=(*A).bounds[i]; } va_end(ap); (*A).base=(ElemType *)malloc(elemtotal*sizeof(ElemType)); if(!(*A).base) exit(OVERFLOW); (*A).constants=(int *)malloc(dim*sizeof(int)); if(!(*A).constants) exit(OVERFLOW); (*A).constants[dim-1]=1; for(i=dim-2; i>=0; --i) (*A).constants[i]=(*A).bounds[i+1]*(*A).constants[i+1]; return OK; } Status DestroyArray(Array *A) { /* 销毁数组A */ if((*A).base) { free((*A).base); (*A).base=NULL; } else return ERROR; if((*A).bounds) { free((*A).bounds); (*A).bounds=NULL; } else return ERROR; if((*A).constants) { free((*A).constants); (*A).constants=NULL; } else return ERROR; return OK; } Status Locate(Array A,va_list ap,int *off) /* Value()、Assign()调用此函数 */ { /* 若ap指示的各下标值合法,则求出该元素在A中的相对地址off */ int i,ind; *off=0; for(i=0; i<A.dim; i++) { ind=va_arg(ap,int); if(ind<0||ind>=A.bounds[i]) return OVERFLOW; *off+=A.constants[i]*ind; } return OK; } Status Value(ElemType *e,Array A,...) /* 在VC++中,...之前的形参不能是引用类型 */ { /* ...依次为各维的下标值,若各下标合法,则e被赋值为A的相应的元素值 */ va_list ap; Status result; int off; va_start(ap,A); if((result=Locate(A,ap,&off))==OVERFLOW) /* 调用Locate() */ return result; *e=*(A.base+off); return OK; } Status Assign(Array *A,ElemType e,...) { /* ...依次为各维的下标值,若各下标合法,则将e的值赋给A的指定的元素 */ va_list ap; Status result; int off; va_start(ap,e); if((result=Locate(*A,ap,&off))==OVERFLOW) /* 调用Locate() */ return result; *((*A).base+off)=e; return OK; } int main() { Array A; int i,j,k,*p,dim=3,bound1=3,bound2=4,bound3=2; /* a[3][4][2]数组 */ ElemType e,*p1; InitArray(&A,dim,bound1,bound2,bound3); /* 构造3*4*2的3维数组A */ p=A.bounds; printf("A.bounds="); for(i=0; i<dim; i++) /* 顺序输出A.bounds */ printf("%d ",*(p+i)); p=A.constants; printf("\nA.constants="); for(i=0; i<dim; i++) /* 顺序输出A.constants */ printf("%d ",*(p+i)); printf("\n%d页%d行%d列矩阵元素如下:\n",bound1,bound2,bound3); for(i=0; i<bound1; i++) { for(j=0; j<bound2; j++) { for(k=0; k<bound3; k++) { Assign(&A,i*100+j*10+k,i,j,k); /* 将i*100+j*10+k赋值给A[i][j][k] */ Value(&e,A,i,j,k); /* 将A[i][j][k]的值赋给e */ printf("A[%d][%d][%d]=%2d ",i,j,k,e); /* 输出A[i][j][k] */ } printf("\n"); } printf("\n"); } p1=A.base; printf("A.base=\n"); for(i=0; i<bound1*bound2*bound3; i++) /* 顺序输出A.base */ { printf("%4d",*(p1+i)); if(i%(bound2*bound3)==bound2*bound3-1) printf("\n"); } DestroyArray(&A); system("PAUSE"); }
广义表定义
广义表是n(n≥0)个元素a1,a2,…,ai,…,an的有限序列。
其中:
①ai--或者是原子或者是一个广义表。
②广义表通常记作:
Ls=( a1,a2,…,ai,…,an)。
③Ls是广义表的名字,n为它的长度。
④若ai是广义表,则称它为Ls的子表。
注意:
①广义表通常用圆括号括起来,用逗号分隔其中的元素。
②为了区分原子和广义表,书写时用大写字母表示广义表,用小写字母表示原子。
③若广义表Ls非空(n≥1),则al是LS的表头,其余元素组成的表(a1,a2,…,an)称为Ls的表尾。
④广义表是递归定义的
(1)广义表常用表示
① E=()
E是一个空表,其长度为0。
② L=(a,b)
L是长度为2的广义表,它的两个元素都是原子,因此它是一个线性表
③ A=(x,L)=(x,(a,b))
A是长度为2的广义表,第一个元素是原子x,第二个元素是子表L。
④ B=(A,y)=((x,(a,b)),y)
B是长度为2的广义表,第一个元素是子表A,第二个元素是原子y。
⑤ C=(A,B)=((x,(a,b)),((x,(a,b)),y))
C的长度为2,两个元素都是子表。
⑥ D=(a,D)=(a,(a,(a,(…))))
D的长度为2,第一个元素是原子,第二个元素是D自身,展开后它是一个无限的广义表。
【例】表L、A、B、C的深度为分别为1、2、3、4,表D的深度为∞。
(3)带名字的广义表表示
如果规定任何表都是有名字的,为了既表明每个表的名字,又说明它的组成,则可以在每个表的前面冠以该表的名字,于是上例中的各表又可以写成:
①E()
②L(a,b)
③A(x,L(a,b))
④B(A(x,L(a,b)),y)
⑤C(A(x,l(a,b)),B(A(x,L(a,b)),y))
⑥D(a,D(a,D(…)))
广义表长度是数第一层括号内的逗号数目可以看到,只有一个元素,
就是((a,b,(),c),d),e,((f),g),所以长度是1,深度是数括号数目,深度是4。
//21:39:55
主要是kmp算法
如何计算next 数组:
next数组下标从1开始计算
next[1] 肯定是 0
next[2] 肯定是 1
next[n] 的情况,将前面n-1个字符,计算从首尾开始组成最大的相同子串的长度,如果找到,那么next值是该长度加1,否则next值是1。
KMP算法的部分匹配值问题。
- "a"的前缀和后缀都为空集,共有元素的长度为0;
- "ab"的前缀为[A],后缀为[B],共有元素的长度为0;
- "aba"的前缀为[a, ab],后缀为[ba, a],共有元素的长度1;
- "abab"的前缀为[a, ab, aba],后缀为[bab, ab, b],共有元素的长度为2;
- "ababa"的前缀为[a, ab, aba, abab],后缀为[baba, aba, ba, a],共有元素为"aba",长度为3;

void getnext(char *s) { int i=0,j=-1; next[0]=-1; int len=strlen(s); while(i<len) { if(s[i]==s[j]||j==-1) { i++; j++; next[i]=j; } else j=next[j]; } }
计算next 的值,同时,也能用于修正next值的数据nextval 求解:
求nextval数组值有两种方法,一种是不依赖next数组值直接用观察法求得,一种方法是根据next数组值进行推理,两种方法均可使用,视更喜欢哪种方法而定。
本文主要分析nextval数组值的第二种方法:
模式串 a b a a b c a c
next值 0 1 1 2 2 3 1 2
nextval值 0 1 0 2 1 3 0 2
1.第一位的nextval值必定为0,第二位如果于第一位相同则为0,如果不同则为1。
2.第三位的next值为1,那么将第三位和第一位进行比较,均为a,相同,则,第三位的nextval值为0。
3.第四位的next值为2,那么将第四位和第二位进行比较,不同,则第四位的nextval值为其next值,为2。
4.第五位的next值为2,那么将第五位和第二位进行比较,相同,第二位的next值为1,则继续将第二位与第一位进行比较,不同,则第五位的nextval值为第二位的next值,为1。
5.第六位的next值为3,那么将第六位和第三位进行比较,不同,则第六位的nextval值为其next值,为3。
6.第七位的next值为1,那么将第七位和第一位进行比较,相同,则第七位的nextval值为0。
7.第八位的next值为2,那么将第八位和第二位进行比较,不同,则第八位的nextval值为其next值,为2。
KMP算法建立在next数组的基础上,计算str 在 s 中出现的次数 合并在main 函数里的getnext

#include <bits/stdc++.h> using namespace std; //KMP 算法 int N; const int maxn = 10010; int nex[maxn]; int main() { scanf("%d", &N); string s,str; while(N--) { memset(nex,-1,sizeof(nex)); cin>>str>>s; int _len = str.length(); int len = s.length(); int j=-1,i=0; while(i<_len) { if(j==-1||str[i]==str[j]) nex[++i]=++j; else j=nex[j]; } i=j=0; int ans =0 ; while(i<len) { if(j==-1||s[i]==str[j]) ++i,++j; else j=nex[j]; if(j == _len) ans++; } cout<<ans<<endl; } return 0; }
如果想了解更多关于KMP算法的应用--------------> Link

#include <bits/stdc++.h> using namespace std; const int maxn = 1000010; char s[maxn]; char s_new[maxn*2]; int mac[maxn*2]; void Manacher() // 求解最长回文子串 { scanf("%s",s); int l = 0; s_new[l++] = ‘$‘; s_new[l++] = ‘#‘; //现在匹配串开始填充两个不同的特殊字符 int len = strlen(s); for(int i=0;i<len;i++) // 然后遍历原来的串,隔一个位置,插入一个 ‘#’ { s_new[l++] = s[i]; s_new[l++] = ‘#‘; } s_new[l] = 0; //匹配串末尾设置为 0 int mx = 0,id=0; for(int i=0;i<l;i++) // mac 匹配数组 { mac[i] = mx>i?min(mac[2*id-1],mx-i):1; // 确定比较的位置 while(s_new[i+mac[i]]==s_new[i-mac[i]]) mac[i]++; if(i+mac[i]>mx) { mx = i + mac[i]; id = i; } } int ans = 0; for(int i=0;i<2*len+2;i++) // 找到 mac里面的最大值,这个值 -1 就是最长回文子串的长度 ans = max(ans,mac[i]-1); printf("%d\n",ans); } int main() { int k; scanf("%d",&k); while(k--) Manacher(); } /* 3 abababa aaaabaa acacdas 7 5 3 */
18:35:17
顺序存储:
typedef struct node{ datatype data; int lchild,rchild; int parent; }Node;
链式存储:
typedef struct BinNode{ datatype data; struct BinNode* lchild; struct BinNode* rchild; }BinNode;
根据前序遍历生成树(链式存储)

void createtree(bintree *t){ datatype c; if((c=getchar()) == ‘#‘) *t = NULL; else{ *t = (bintree)malloc(sizeof(BinNode)); (*t)->data = c; createtree(&(*t)->lchild); createtree(&(*t)->rchild); } }
要用数组生成的话,直接在函数里面加入一个参数引用代替getchar() 就好。
采取结构链式存储
typedef char datatype; typedef struct BinNode{ datatype data; struct BinNode* lchild; struct BinNode* rchild; }BinNode; typedef BinNode* bintree;
中序遍历:左根右后序遍历:左右根 前序遍历 :根左右递归型遍历:前序遍历
void preorder(bintree t){ if(t){ printf("%c ",t->data); //根 preorder(t->lchild);//左 preorder(t->rchild);//右 } }
需要进行预处理

#define SIZE 100 typedef struct seqstack{ bintree data[SIZE]; int tag[SIZE]; //为后续遍历准备的 int top; //top为数组的下标 }seqstack; void push(seqstack *s,bintree t){ if(s->top == SIZE){ printf("the stack is full\n"); }else{ s->top++; s->data[s->top]=t; } } bintree pop(seqstack *s){ if(s->top == -1){ return NULL; }else{ s->top--; return s->data[s->top+1]; } }
前序遍历

void preorder_dev(bintree t){ seqstack s; s.top = -1; //因为top在这里表示了数组中的位置,所以空为-1 if(!t){ printf("the tree is empty\n"); }else{ while(t || s.stop != -1){ while(t){ //只要结点不为空就应该入栈保存,与其左右结点无关 printf("%c ",t->data); push(&s,t); t= t->lchild; } t=pop(&s); t=t->rchild; } } }
中序遍历

void midorder(bintree t){ seqstack s; s.top = -1; if(!t){ printf("the tree is empty!\n"); }else{ while(t ||s.top != -1){ while(t){ push(&s,t); t= t->lchild; } t=pop(&s); printf("%c ",t->data); t=t->rchild; } } }
后序遍历

void postorder_dev(bintree t){ seqstack s; s.top = -1; if(!t){ printf("the tree is empty!\n"); }else{ while(t || s.top != -1){ //栈空了的同时t也为空。 while(t){ push(&s,t); s.tag[s.top] = 0; //设置访问标记,0为第一次访问,1为第二次访问 t= t->lchild; } if(s.tag[s.top] == 0){ //第一次访问时,转向同层右结点 t= s.data[s.top]; //左走到底时t是为空的,必须有这步! s.tag[s.top]=1; t=t->rchild; }else { while (s.tag[s.top] == 1){ //找到栈中下一个第一次访问的结点,退出循环时并没有pop所以为其左子结点 t = pop(&s); printf("%c ",t->data); } t = NULL; //必须将t置空。跳过向左走,直接向右走 } } } }

bool InsetBST(BiTree &T,int k) { BitNode* p; if(!SearchBST(T,k,NULL,p)) { BitNode * temp=new BitNode; temp->data=k; temp->lchild=temp->rchild=NULL; if(!p) //只有树为空时,此时的p才为NULL。看到这里应该明白SearchBST(T,k,pre,p)这些参数的意义了吧 { T=temp; } else { if(k<p->data) //如果不为空树,加入的key值就和p相比较,小于就是他的左孩子,否子为右孩子 p->lchild=temp; else { p->rchild=temp; } } return 0; } else { return false; } }

bintree search_tree(bintree t,datatype x){ if(!t){ return NULL; } if(t->data == x){ return t; }else{ if(!search_tree(t->lchild,x)){ return search_tree(t->rchild,x); } return t; } }

int hight_tree(bintree t){ int h,left,right; if(!t){ return 0; } left = hight_tree(t->lchild); right = hight_tree(t->rchild); h = (left>right?left:right)+1; return h; }
n0:度为0的结点数,n1:度为1的结点 n2:度为2的结点数。 N是总结点。
在二叉树中:
n0=n2+1;
N=n0+n1+n2

int count_tree(bintree t){ if(t){ return (count_tree(t->lchild)+count_tree(t->rchild)+1); } return 0; }

int leaf(BiTree root) { static int leaf_count = 0; if (NULL != root) { leaf(root->lchild); leaf(root->rchild); if (root->lchild == NULL && root->rchild == NULL) leaf_count++; } return leaf_count; }
优化AVL树:
//TODO 22:07:35
.高度为 h 的 AVL 树,节点数 N 最多2^h ? 1; 最少N(h)=N(h? 1) +N(h? 2) + 1。
含有 n 个节点,不相似的二叉树 有 : 1/(n+1)*C(n,2n)种;
树、森林与二叉树的转换
1、树转换为二叉树
由于二叉树是有序的,为了避免混淆,对于无序树,我们约定树中的每个结点的孩子结点按从左到右的顺序进行编号。
将树转换成二叉树的步骤是:
(1)加线。就是在所有兄弟结点之间加一条连线;
(2)抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
(3)旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
树转换为二叉树的过程示意图
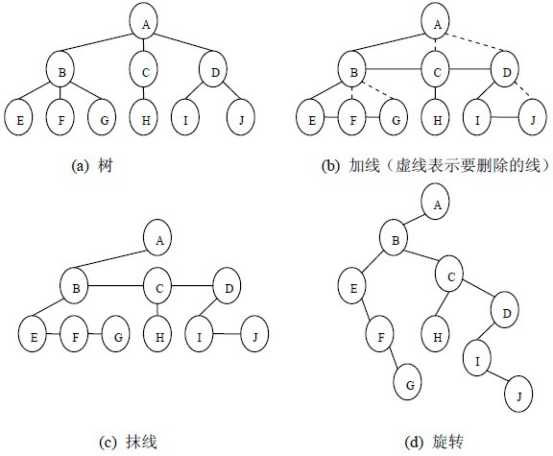
2、森林转换为二叉树
森林是由若干棵树组成,可以将森林中的每棵树的根结点看作是兄弟,由于每棵树都可以转换为二叉树,所以森林也可以转换为二叉树。
将森林转换为二叉树的步骤是:
(1)先把每棵树转换为二叉树;
(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点,用线连接起来。当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。
森林转换为二叉树的转换过程示意图
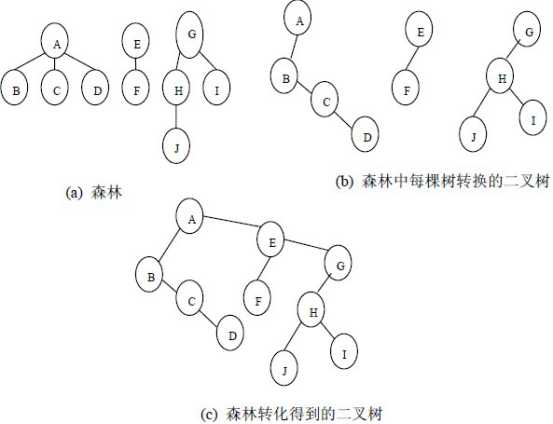
3、二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,其步骤是:
(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
(2)删除原二叉树中所有结点与其右孩子结点的连线;
(3)整理(1)和(2)两步得到的树,使之结构层次分明。
二叉树转换为树的过程示意图
4、二叉树转换为森林
二叉树转换为森林比较简单,其步骤如下:
(1)先把每个结点与右孩子结点的连线删除,得到分离的二叉树;
(2)把分离后的每棵二叉树转换为树;
(3)整理第(2)步得到的树,使之规范,这样得到森林。
根据树与二叉树的转换关系以及二叉树的遍历定义可以推知,树的先序遍历与其转换的相应的二叉树的先序遍历的结果序列相同;树的后序遍历与其转换的二叉树的中序遍历的结果序列相同;树的层序遍历与其转换的二叉树的后序遍历的结果序列相同。由森林与二叉树的转换关系以及森林与二叉树的遍历定义可知,森林的先序遍历和中序遍历与所转换得到的二叉树的先序遍历和中序遍历的结果序列相同。
设图中 节点数 n , 边数 m
如果用邻接矩阵存储图:空间复杂度 O(n^2)
邻接表存储图 : 空间复杂度 O(n+m)

#include<stdio.h> #include<string.h> int head[100100];//表头,head[i]代表起点是i的边的编号 int cnt;//代表边的编号 struct s { int u;//记录边的起点 int v;//记录边的终点 int w;//记录边的权值 int next;//指向上一条边的编号 }edge[100010]; void add(int u,int v,int w)//向所要连接的表中加入边 { edge[cnt].u=u; edge[cnt].v=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++; } int main() { int n; while(scanf("%d",&n)!=EOF) { int i; cnt=0; memset(head,-1,sizeof(head));//清空表头数组 for(i=0;i<n;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); add(u,v,w); } int u,v,w; scanf("%d",&u); for(i=head[u];i!=-1;i=edge[i].next)//输出所有与起点为u相连的边的终点和权值 { v=edge[i].v; w=edge[i].w; printf("%d %d\n",v,w); } } return 0; }
邻接矩阵:二维数组
由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步,直到不存在入度为0的顶点为止。
(1) 选择一个入度为0的顶点并输出之;
(2) 从网中删除此顶点及所有出边。
循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列。

#include <bits/stdc++.h> using namespace std; #define maxn 100//可以根据题目条件进行更改 int edge[maxn][maxn]; int book[maxn]; int point_num; int edge_num; bool check_point(int v)//确定这个点是不是没有入度; { for(int i=1;i<=point_num;i++) if(edge[i][v]==1&&(i!=v))//如果有入度,返回false,i==v时没有啥实际意义 return false; return true; } void del_edge(int v)//删除以这个点为起始点的所有边 { fill(edge[v],edge[v]+point_num,0);//fill灵活用法,用for循环效果一样,时间复杂度相同 } int main() { memset(book,0,sizeof(book)); scanf("%d",&point_num); scanf("%d",&edge_num);//点的个数,边的个数,设为宏观变量,比较好操作 memset(edge,0,sizeof(edge)); for(int i=1;i<=edge_num;i++) { int s_point,e_point; scanf("%d%d",&s_point,&e_point); edge[s_point][e_point]=1; } int i;//下面循环代码肯定是能优化的,不过我一时半会想不起来,欢迎留言,私信我 for(;i<=point_num;i++) { if(check_point(i)&&book[i]==0) { book[i]=1; cout<<i<<" "; del_edge(i);//删除bian i=1; } } for(int i=1;i<=point_num;i++) { if(book[i]==0) cout<<i<<endl; }//扫尾工作,最后可能会留下一个点;输出格式自己搞! }
拓扑排序题目,以及拓扑代码优化----------------------> Link
根据拓扑排序实现关键路径:

typedef struct ArcNode { int adjvex; //该弧指向的顶点位置 struct ArcNode * nextarc; //指向下一个表结点 int info; //权值信息 }ArcNode; //边结点类型 Status TopologicalOrder(ALGraph G, Stack &T) { // 有向网G采用邻接表存储结构,求各顶点事件的最早发生时间ve(全局变量)。 // T为拓扑序列定点栈,S为零入度顶点栈。 // 若G无回路,则用栈T返回G的一个拓扑序列,且函数值为OK,否则为ERROR。 Stack S; int count=0,k; char indegree[40]; ArcNode *p; InitStack(S); FindInDegree(G, indegree); // 对各顶点求入度indegree[0..vernum-1] for (int j=0; j<G.vexnum; ++j) // 建零入度顶点栈S if (indegree[j]==0) Push(S, j); // 入度为0者进栈 InitStack(T);//建拓扑序列顶点栈T count = 0; for(int i=0; i<G.vexnum; i++) ve[i] = 0; // 初始化 while (!StackEmpty(S)) { Pop(S, j); Push(T, j); ++count; // j号顶点入T栈并计数 for (p=G.vertices[j].firstarc; p; p=p->nextarc) { k = p->adjvex; // 对j号顶点的每个邻接点的入度减1 if (--indegree[k] == 0) Push(S, k); // 若入度减为0,则入栈 if (ve[j]+p->info > ve[k]) ve[k] = ve[j]+p->info; }//for *(p->info)=dut(<j,k>) } if(count<G.vexnum) return ERROR; // 该有向网有回路 else return OK; } Status CriticalPath(ALGraph G) { // G为有向网,输出G的各项关键活动。 Stack T; int a,j,k,el,ee,dut; char tag; ArcNode *p; if (!TopologicalOrder(G, T)) return ERROR; for(a=0; a<G.vexnum; a++) vl[a] = ve[G.vexnum-1]; // 初始化顶点事件的最迟发生时间 while (!StackEmpty(T)) // 按拓扑逆序求各顶点的vl值 for (Pop(T, j), p=G.vertices[j].firstarc; p; p=p->nextarc) { k=p->adjvex; dut=p->info; //dut<j,k> if (vl[k]-dut < vl[j]) vl[j] = vl[k]-dut; } for (j=0; j<G.vexnum; ++j) // 求ee,el和关键活动 for (p=G.vertices[j].firstarc; p; p=p->nextarc) { k=p->adjvex;dut=p->info; ee = ve[j]; el = vl[k]-dut; tag = (ee==el) ? ‘*‘ : ‘ ‘; printf(j, k, dut, ee, el, tag); // 输出关键活动 } return OK; }

#include <stdio.h> #include <stdlib.h> #define MaxVerNum 20 int visited[MaxVerNum]; typedef char VertexType; typedef struct ArcNode { int adjvex; //该弧指向的顶点位置 struct ArcNode * nextarc; //指向下一个表结点 int info; //权值信息 }ArcNode; //边结点类型 typedef struct VNode { VertexType data; int indegree; ArcNode * firstarc; }VNode, Adjlist[MaxVerNum]; typedef struct { Adjlist vertices; //邻接表 int vernum, arcnum; //顶点数和弧数 }ALGraph; //查找符合的数据在数组中的下标 int LocateVer(ALGraph G, char u) { int i; for(i = 0; i < G.vernum; i++) { if(u == G.vertices[i].data) return i; } if(i == G.vernum) { printf("Error u!\n"); exit(1); } return 0; } //常见图的邻接矩阵 void CreateALGraph(ALGraph &G) { int i, j, k, w; char v1, v2; ArcNode * p; printf("输入顶点数和弧数: "); scanf("%d %d", &G.vernum, &G.arcnum); printf("请输入顶点!\n"); for(i = 0; i < G.vernum; i++) { printf("请输入第 %d 个顶点: \n", i); fflush(stdin); scanf("%c", &G.vertices[i].data); G.vertices[i].firstarc = NULL; G.vertices[i].indegree = 0; } for(k = 0; k < G.arcnum; k++) { printf("请输入弧的顶点和相应权值(v1, v2, w): \n"); //清空输入缓冲区 fflush(stdin); scanf("%c %c %d", &v1, &v2, &w); i = LocateVer(G, v1); j = LocateVer(G, v2); p = (ArcNode *)malloc(sizeof(ArcNode)); p->adjvex = j; p->info = w; p->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p; G.vertices[j].indegree++; //vi->vj, vj入度加1 } return; } //求图的关键路径函数 void CriticalPath(ALGraph G) { int i, k, e, l; int * Ve, * Vl; ArcNode * p; //***************************************** //以下是求时间最早发生时间 //***************************************** Ve = new int [G.vernum]; Vl = new int [G.vernum]; for(i = 0; i < G.vernum; i++) //前推 Ve[i] = 0; for(i = 0; i < G.vernum; i++) { ArcNode * p = G.vertices[i].firstarc; while(p != NULL) { k = p->adjvex; if(Ve[i] + p->info > Ve[k]) Ve[k] = Ve[i]+p->info; p = p->nextarc; } } //***************************************** //以下是求最迟发生时间 //***************************************** for(i = 0; i < G.vernum; i++) Vl[i] = Ve[G.vernum-1]; for(i = G.vernum-2; i >= 0; i--) //后推 { p = G.vertices[i].firstarc; while(p != NULL) { k = p->adjvex; if(Vl[k] - p->info < Vl[i]) Vl[i] = Vl[k] - p->info; p = p->nextarc; } } //****************************************** for(i = 0; i < G.vernum; i++) { p = G.vertices[i].firstarc; while(p != NULL) { k = p->adjvex; e = Ve[i]; //最早开始时间为时间vi的最早发生时间 l = Vl[k] - p->info; //最迟开始时间 char tag = (e == l) ? ‘*‘ : ‘ ‘; //关键活动 printf("(%c, %c), e = %2d, l = %2d, %c\n", G.vertices[i].data, G.vertices[k].data, e, l, tag); p = p->nextarc; } } delete [] Ve; delete [] Vl; } void main() { ALGraph G; printf("以下是查找图的关键路径的程序。\n"); CreateALGraph(G); CriticalPath(G); }

#include <iostream> #include <cstdio> #include <cstring> #include <stack> #include <queue> #define Inf 10000000 using namespace std; struct Renwu { int a; int b; int ti; int id; }renwu[10000]; struct cmp { bool operator()(struct Renwu t1,struct Renwu t2) { if(t1.a<t2.a) return 0; else if(t1.a==t2.a&&t1.id>t2.id) return 0; else return 1; } }; int main() { int n,m,time[105][105],indegree[105],outdegree[105]; scanf("%d%d",&n,&m); memset(time,0,sizeof(time)); memset(indegree,0,sizeof(indegree)); for(int i=1;i<=m;i++) { scanf("%d%d%d",&renwu[i].a,&renwu[i].b,&renwu[i].ti); time[renwu[i].a][renwu[i].b]=renwu[i].ti; indegree[renwu[i].b]++; outdegree[renwu[i].a]++; renwu[i].id=i; } stack<int> s; int cnt=0,ve[105]; memset(ve,0,sizeof(ve)); for(int i=1;i<=n;i++) { if(indegree[i]==0) {s.push(i); cnt++;} } int u; while(!s.empty()) { u=s.top(); s.pop(); for(int i=1;i<=n;i++) { if(time[u][i]!=0) { ve[i]=max(ve[i],ve[u]+time[u][i]); if(--indegree[i]==0) {s.push(i); cnt++;} } } } if(cnt!=n) printf("0\n"); else { int ma=0; for(int i=1;i<=n;i++) { ma=max(ve[i],ma); } printf("%d\n",ma); int vl[105]; for(int i=1;i<=n;i++) { vl[i]=Inf; } for(int i=1;i<=n;i++) { if(outdegree[i]==0) {vl[i]=ma; s.push(i);} } while(!s.empty()) { u=s.top(); s.pop(); for(int i=1;i<=n;i++) { if(time[i][u]!=0) { vl[i]=min(vl[i],vl[u]-time[i][u]); if(--outdegree[i]==0) s.push(i); } } } priority_queue<struct Renwu,vector<struct Renwu>,cmp> q; for(int i=1;i<=m;i++) { if(ve[renwu[i].a]==vl[renwu[i].a]&&ve[renwu[i].b]==vl[renwu[i].b]&&vl[renwu[i].b]-time[renwu[i].a][renwu[i].b]==ve[renwu[i].a]) q.push(renwu[i]); } struct Renwu t; while(!q.empty()) { t=q.top(); q.pop(); printf("%d->%d\n",t.a,t.b); } } }

#include <iostream> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int MAXN=1000002; vector<int> g[MAXN]; bool vis[MAXN]; int n,m; void dfs(int s) //递归深搜 { vis[s]=true; for(int i=0; i<g[s].size(); ++i) { if(vis[g[s][i]]) g[s].erase(g[s].begin()+i);//删除图中已经遍历过的点,可提高遍历速度 else dfs(g[s][i]); } } bool judge() //判断是否所有点已被遍历过 { for(int i=1; i<=n; ++i) if(!vis[i]) return false; return true; } int main() { while(~scanf("%d%d",&n,&m)) { for(int i=1; i<=n; ++i) g[i].clear(); for(int i=0; i<m; ++i) { int a,b; scanf("%d%d",&a,&b); g[a].push_back(b); //无向图转化为有向图,正反两次存入连接表。 g[b].push_back(a); } memset(vis,false,sizeof(vis)); dfs(1); if(judge()) printf("yes\n"); else printf("no\n"); } return 0; }

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <string> #include <vector> #include <map> #include <algorithm> using namespace std; int set[1000005]; int find(int x){ returnx==set[x]?x:(set[x]=find(set[x])); //递归查找集合的代表元素,含路径压缩。 } int main() { int n,m,i,x,y; scanf("%d%d",&n,&m); for(i=1;i<1000005;++i) //初始化个集合,数组值等于小标的点为根节点。 set[i]=i; for(i=0;i<m;++i){ int a,b; scanf("%d%d",&a,&b); int fx=find(a),fy=find(b); set[fx]=fy; //合并有边相连的各个连通分量 } int cnt=0; for(i=1;i<=n;++i) //统计集合个数,即为连通分量个数,为一时,图联通。 if(set[i]==i) ++cnt; if(cnt==1) printf("yes\n"); else printf("no\n"); return 0; }

#include <iostream> #include <cstdio> #include <vector> #include <queue> using namespace std; const int maxn = 1000 + 5; int n,m; int my_index; vector<int >G[maxn]; bool vis[maxn]; void bfs(int u){ queue<int >Q; Q.push(u); while(!Q.empty()){ int s = Q.front();Q.pop(); vis[s] = true; my_index++; for(int i = 0;i < G[s].size(); i++){ int v = G[s][i]; if(!vis[v])Q.push(v); } } } int main(){ scanf("%d%d",&n,&m); for(int i = 1;i <= m; i++){ int a,b; scanf("%d%d",&a,&b); G[a].push_back(b); G[b].push_back(a); } bfs(1); if(my_index == n)printf("Yes\n"); else printf("No\n"); }
图的连通性解决的过程中,可以一并结局的问题是回路问题&图的割集

#include<iostream> using namespace std; struct L { int v; L *next; }; class HEAD { public: int id; L *next; HEAD(){ id=0; next=NULL;} }; HEAD head[1000]; int dfn[1000],low[1000],t; bool lock[1000],C[1000]; void find(int father,int v) { int count=0; /*统计v的孩子数*/ dfn[v]=low[v]=++t; /*将访问时间赋给dfn[v]和low[v]*/ lock[v]=false; /*标记v点已经访问过,不能再被访问*/ for(L *p=head[v].next;p!=NULL;p=p->next) { if(lock[p->v]) /*如果v的直接后继节点没有访问过,则对其遍历*/ { find(v,p->v); /*对v的直接后继遍历*/ count++; /* 孩子数+1 */ if(low[v]>low[p->v]) /*如果v的孩子能追溯到更早的祖先,则v也能追溯到*/ low[v]=low[p->v]; } else if(p->v!=father&&low[p->v]<low[v]) /*如果v的直接孩子节点已经被访问过*/ low[v]=low[p->v]; if(!father&&count>1) /*如果当前节点是DFS遍历到的第一个节点,则判断其是否有多个孩子*/ C[v]=true; else if(father&&dfn[v]<=low[p->v]) /*否则判断其后继能否追溯到v的祖先*/ C[v]=true; } } int main() { int n,i,a,b; cin>>n; while(cin>>a>>b&&a&&b) /*建立邻接表,输入无向图边每条a b,以0 0结束*/ { L *p=new L; p->next=head[b].next; head[b].next=p; p->v=a; p=new L; p->next=head[a].next; head[a].next=p; p->v=b; head[b].id++; head[a].id++; } memset(lock,true,sizeof(lock)); memset(dfn,0,sizeof(int)*1000); memset(C,0,sizeof(C)); /*C数组用来标记那些点是割点,刚开始全部置为false*/ t=0; /*访问时间*/ find(0,1);/*开始对1号点DFS,第一个遍历的前驱节点设为0*/ for(i=1;i<=n;i++) /*输入割点*/ if(C[i]) cout<<i<<‘ ‘; cout<<endl; }
若图G中存在这样一条路径,使得它恰通过G中每条边一次,则称该路径为欧拉路径。若该路径是一个圈,则称为欧拉(Euler)回路。
具有欧拉回路的图称为欧拉图(简称E图)。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。
以下判断基于此图的基图连通。
无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
判断欧拉路是否存在的方法
有向图:图连通,有一个顶点出度大入度1,有一个顶点入度大出度1,其余都是出度=入度。
无向图:图连通,只有两个顶点是奇数度,其余都是偶数度的。
判断欧拉回路是否存在的方法
有向图:图连通,所有的顶点出度=入度。
无向图:图连通,所有顶点都是偶数度。
程序实现一般是如下过程:
1.利用并查集判断图是否连通,即判断p[i] < 0的个数,如果大于1,说明不连通。
2.根据出度入度个数,判断是否满足要求。
3.利用dfs输出路径。
22:45:42
for(k=1; k<=n; k++)
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
if(e[i][k]<inf && e[k][j]<inf && e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];

Problem Description 在每年的校赛里,所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候,却是非常累的!所以现在他们想要寻找最短的从商店到赛场的路线,你可以帮助他们吗? Input 输入包括多组数据。每组数据第一行是两个整数N、M(N<=100,M<=10000),N表示成都的大街上有几个路口,标号为1的路口是商店所在地,标号为N的路口是赛场所在地,M则表示在成都有几条路。N=M=0表示输入结束。接下来M行,每行包括3个整数A,B,C(1<=A,B<=N,1<=C<=1000),表示在路口A与路口B之间有一条路,我们的工作人员需要C分钟的时间走过这条路。 输入保证至少存在1条商店到赛场的路线。 Output 对于每组输入,输出一行,表示工作人员从商店走到赛场的最短时间 Sample Input 2 1 1 2 3 3 3 1 2 5 2 3 5 3 1 2 0 0 Sample Output 3 2 ------------------------------------------------ #include <stdio.h> #include <string.h> #define INF 0x3f3f3f3f int dis[110];//dis[i]表示从起点到i的距离 int map[110][110];//map[i][j]表示从i到j的距离 bool used[110];//标记某点是否用过 int n,m; void Dijkstra(int x) { int pos=x; for(int i=1;i<=n;i++) { dis[i]=map[x][i]; } dis[x]=0;//本身到本身为0 used[x]=true; for (int i=2;i<=n;i++)//扫剩下的点(作为大循环) { int min=INF; for(int j=1;j<=n;j++)//找出当前最距离近的点 { if(!used[j]&&dis[j]<min) { min=dis[j]; pos=j; } } used[pos]=true; dis[pos]=min; for(int j=1;j<=n;j++) { if(!used[j]&&dis[j]>dis[pos]+map[pos][j])//画个图就知道了 { dis[j]=dis[pos]+map[pos][j]; } } } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { if(n==0&&m==0) break; memset(dis,INF,sizeof(dis)); memset(used,false,sizeof(used)); for(int i=1;i<=n;i++)//初始化 { for(int j=1;j<=n;j++) { map[i][j]=INF; } } while(m--) { int a,b,p; scanf("%d%d%d",&a,&b,&p); if(map[a][b]>p)//不知道为啥必须得加这个条件,不加就wa。。 { map[a][b]=p; map[b][a]=p;//这里注意点,双向都赋值 } } Dijkstra(1);//起点为1 printf("%d\n",dis[n]);//终点为n } return 0; }
同时,对于Dj单源最短路,有一个非常简单,但是能减少不少代码量的方法: mini = dis[cur=j];
void dijkstra(int s)
{
memset(vis,0,sizeof(vis));
int cur=s;
dis[cur]=0;
vis[cur]=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
if(!vis[j] && dis[cur] + map[cur][j] < dis[j]) //未被标记且比已知的短,可更新
dis[j]=dis[cur] + map[cur][j] ;
int mini=INF;
for(int j=0;j<n;j++)
if(!vis[j] && dis[j] < mini) //选择下一次到已知顶点最短的点。
mini=dis[cur=j];
vis[cur]=true;
}
}
也可以用优先队列进行优化:
void dijkstra(int s)
{
priority_queue <node>q;
for(int i=0;i<n;i++)
d[i]=INF;
d[s]=0;
q.push_back(node(0,s));
while(!q.empty())
{
node x=q.top();
q.pop();
int u=x.u;
for(int i=0;i<G[u].size();i++)
{
node e=G[u][i];
if(d[e.u]>d[u]+e.d)
{
d[e.u]=x.d+e.d;
pi[e.u]=u;
q.push_bacK(node(d[e.u],e.u));
}
}
}
}
最短路径还能不仅能显示单源到某一点的最短距离,还能计算花费和输出行走路径
Dj + 路径输出

#include <cstdio> #include <cstring> #include <cstdlib> #include <algorithm> #define N 1005 #define INF 0x3f3f3f3f using namespace std; int m, n; int map[N][N]; int dis[N],pre[N]; int vis[N]; void init() { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (i == j) map[i][j] = 0; else map[i][j] = INF; } } } void creatgraph() { int t1, t2, t3; for (int i = 0; i < m; i++) { scanf("%d%d%d", &t1, &t2, &t3);//两个顶点和权值 if (map[t1][t2] > t3)//防止重复输入相同节点,但是权值不同 map[t1][t2] = t3; } } void dijkstra(int start) { /*下边初始化dis,vis数组*/ for (int i = 1; i <= n; i++) { dis[i] = map[start][i]; if (dis[i] >= INF) pre[i] = -1;//若不直接连通,记为-1 else pre[i] = start;//start到i的路径中i的前驱均初始化为start } memset(vis, 0, sizeof(vis)); pre[start] = -1;//起点的前驱初始化为-1 vis[start] = 1;//标记第一个点 for (int i = 1; i <= n - 1; i++)//循环n-1次 { /*找出离起点最近的点*/ int minn = INF, k = -1; for (int j = 1; j <= n; j++) { if (!vis[j] && dis[j] < minn) { minn = dis[j]; k = j; } } vis[k] = 1; for (int i = 1; i <= n; i++) { if (!vis[i] && map[k][i] < INF) { if (dis[i] > dis[k] + map[k][i]) { dis[i] = dis[k] + map[k][i];//松弛操作,找到媒介使得出现新的最短路 pre[i] = k;//k作为i的前驱 } } } } } void printpath(int x) { if (pre[x] != -1) { printpath(pre[x]); printf("->"); } printf("%d", x); //下边为倒序输出路径 /*int tmp = x; while (tmp != 1) { printf("%d->", tmp); tmp = pre[tmp]; } printf("%d", 1);*/ } void print() { for (int i = 1; i <= n; i++) { printf("最短路为:%d\n", dis[i]); printf("最短路径为:"); printpath(i); printf("\n"); } } int main() { while (scanf("%d%d", &n, &m) != EOF)//n个顶点,m条边 { int start; init();//初始化地图 creatgraph();//建图 scanf("%d", &start);//输入起点 dijkstra(start);//核心迪杰斯特拉算法 print();//输出最短路结果 } return 0; }
Dj + 花费计算

#include<iostream> using namespace std; #include<string.h> #include<algorithm> #include<stack> #define maxn 0x7fffffff int mat[505][505],vis[505],pay[505][505]; int dis[505],cost[505],n,m,path[505]; //最短路 + 路径输出 void dijkstra(int s) { int i,j; for(i=0;i<n;i++) { dis[i]=mat[s][i]; cost[i]=pay[s][i]; vis[i]=0; if(dis[i]!=maxn) path[i]=s; else path[i]=-1; } vis[s]=1; dis[s]=0; cost[s]=0; for(i=1;i<n;i++) { int k=s,u=maxn; for(j=0;j<n;j++) { if(!vis[j]&&dis[j]<u) { u=dis[j]; k=j; } } vis[k]=1; for(j=0;j<n;j++) { if(!vis[j]&&mat[k][j]!=maxn) { if(dis[j]>dis[k]+mat[k][j]) { dis[j]=dis[k]+mat[k][j]; cost[j]=cost[k]+pay[k][j]; path[j]=k; } else if(dis[j]==dis[k]+mat[k][j]) { if(cost[j]>cost[k]+pay[k][j]) { cost[j]=cost[k]+pay[k][j]; path[j]=k; } } } } } } void print(int s,int t) { stack<int>q; while(t!=s) { q.push(t); t=path[t]; } q.push(t); while(!q.empty()) { cout<<q.top()<<" "; q.pop(); } } int main() { int s,t,a,b,d,w,i,j; cin>>n>>m>>s>>t; for(i=0;i<n;i++) for(j=0;j<n;j++) mat[i][j]=pay[i][j]=maxn; // for(i=0;i<m;i++) { cin>>a>>b>>d>>w; if(mat[a][b]>d) { mat[a][b]=mat[b][a]=d; pay[a][b]=pay[b][a]=w; } else if(mat[a][b]==d) { if(pay[a][b]>w) pay[a][b]=pay[b][a]=w; } // 输入进行处理,最短路 } dijkstra(s); // 寻找从 s 开始 单源最短路 print(s,t);// 输出路径, S 到 T 的路径 cout<<dis[t]<<" "<<cost[t]<<endl; // dist 指的是 距离 dis[t] 指的是花费 return 0; }
但是,以上的所有算法,在面对负权回路,就会束手无策了 ,Bellman - Ford 负权回路的领跑者!

#include<iostream> #include<cstdio> using namespace std; #define MAX 0x3f3f3f3f #define N 1010 int nodenum, edgenum, original; //点,边,起点 typedef struct Edge //边 { int u, v; int cost; }Edge; Edge edge[N]; int dis[N], pre[N]; bool Bellman_Ford() { for(int i = 1; i <= nodenum; ++i) //初始化 dis[i] = (i == original ? 0 : MAX); for(int i = 1; i <= nodenum - 1; ++i) for(int j = 1; j <= edgenum; ++j) if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反~) { dis[edge[j].v] = dis[edge[j].u] + edge[j].cost; pre[edge[j].v] = edge[j].u; } bool flag = 1; //判断是否含有负权回路 for(int i = 1; i <= edgenum; ++i) if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost) { flag = 0; break; } return flag; } void print_path(int root) //打印最短路的路径(反向) { while(root != pre[root]) //前驱 { printf("%d-->", root); root = pre[root]; } if(root == pre[root]) printf("%d\n", root); } int main() { scanf("%d%d%d", &nodenum, &edgenum, &original); pre[original] = original; for(int i = 1; i <= edgenum; ++i) { scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost); } if(Bellman_Ford()) for(int i = 1; i <= nodenum; ++i) //每个点最短路 { printf("%d\n", dis[i]); printf("Path:"); print_path(i); } else printf("have negative circle\n"); return 0; }
如果想了解更多---------------------> Link
Prim:
#include<iostream>
#include<fstream>
using namespace std;
#define INF 0x3f3f3f3f
const int maxn = 117;
int m[maxn][maxn];
int vis[maxn], low[maxn];
int n;
int prim()
{
vis[1] = 1;
int sum = 0;
int pos, minn;
pos = 1;
for(int i = 1; i <= n; i++)
{
low[i] = m[pos][i];
}
for(int i = 1; i < n; i++)
{
minn = INF;
for(int j = 1; j <= n; j++)
{
if(!vis[j] && minn > low[j])
{
minn = low[j];
pos = j;
}
}
sum += minn;
vis[pos] = 1;
for(int j = 1; j <= n; j++)
{
if(!vis[j] && low[j] > m[pos][j])
{
low[j] = m[pos][j];
}
}
}
return sum;
}
int main()
{
scanf("%d",&n);
int ms = n*(n-1)/2;
int x,y,cost,tes;
for(int i = 1; i <= n ;i++ )
for(int j = 1; j <= n; j++)
m[i][j] = INF;
for(int i = 1; i <= ms ; i++)
{
cin>>x>>y>>cost>>tes;
m[x][y] = m[y][x] = tes==1?0:cost;
}
cost = prim();
cout<< cost << endl;
return 0;
}
Kruskal:
#include<bits/stdc++.h>
using namespace std;
const int MAX=1000;
int father[MAX];
typedef struct
{
int u;
int v;
int w;
}edge;// u,v,w分别代表点,点,对应的边的长度
edge e[MAX];
int n,m;
int sum=0,counts=0;//路径和计数器
void initial(int n) //初始化
{
for(int i=1;i<=n;i++)
father[i]=i;
}
int find(int x) //查找
{
while(father[x]!=x)
x=father[x];
return father[x];// return x==father[x]?father[x]:find(father[x]);
}
int combine(int a,int b) //合并
{
int tmpa=find(a);
int tmpb=find(b);
if(tmpa!=tmpb)
{
father[tmpa]=tmpb;//遵循以右为尊原则,也可以以左为尊
return 1;
}//认祖归宗,找不到就另开山头,
/*
if(tmpa<tmpb)
father[tmpb]=tmpa;
else
father[tmpa]=tmpb;
*/
return 0;
}
bool cmp(edge a,edge b)
{
return a.w<b.w;//快速排序的比较函数
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1,cmp);
initial(n);
for(int i=1;i<=m;i++)
if(combine(e[i].u,e[i].v))//祖宗一样就说明已经联通,不需要在计算,否则就加入并查集中
{
counts++;
sum+=e[i].w;
if(counts==n-1)//最小生成树,最短路径,边只要有n-1条
break;
}
cout<<sum<<endl;//输出最小花费
}
在这里不得不提到并查集,判断集合个数非常简单的方式:

#include<bits/stdc++.h> using namespace std; int father[105]; int maps[110][110]; int n, m , k; int finds(int x) { if(x!=father[x]) father[x]=finds(father[x]); return father[x]; } void combine(int x,int y,int t) { if(t==1) { int a=finds(x); int b=finds(y); if(a==b) return; if(a<b) father[b]=a; else father[a]=b; } else { maps[x][y] = maps[y][x] = -1; } } void init() { for(int i=0;i<=n;i++) father[i]=i; } int main() { scanf("%d%d%d",&n,&m,&k); init(); memset(maps,0,sizeof(maps)); for(int i=1;i<=m;i++) { int x,y,t; scanf("%d%d%d",&x,&y,&t); combine(x,y,t); } int x,y; for(int i=0;i<k;i++) { cin>>x>>y; if(finds(x)==finds(y)&&maps[x][y]!=-1) { printf("No problem\n"); } else if(finds(x)==finds(y)&&maps[x][y]==-1) { printf("OK but...\n"); } else if(finds(x)!=finds(y)&&maps[x][y]==-1) { printf("No way\n"); } else printf("OK\n"); } }
写在最后:
实在抱歉,暂时只能想起来的基础部分只有这么多了,还有许多详细的内容没有填充上去,如果您有好的建议,希望不吝赐教,请尽管在评论区发表,或者私信给我,附加上您希望添加的内容,希望能在各位斧正下尽快完善了这个文章。
有许多部分的内容会对于初学者来说会有那么一点不好理解,如果可能的话,希望初学者在查阅并且学习的过程中,能够整理下来自己存在理解障碍的地方或者自己想要完善的部分,尽可能利用百度。谷歌等工具理解这些内容,最后如果有可能的话,能将你们整理的适合添加的内容分享给我一部分,最好能指出希望修改的部分,我的邮箱 hoodychen@qq.com。
还有,希望大家能给个关注,谢谢各位。
标签:第一个 base 不同的 缓冲区 col ase cout idt count
原文地址:http://www.cnblogs.com/masterchd/p/7987371.html