标签:log src long 2-2 bsp 不同 http name amp
这道题是 BZOJ 2301 Problem b 的加强版
不同的是外面要套一个枚举质数,因为我们不知道GCD是哪个
答案就是
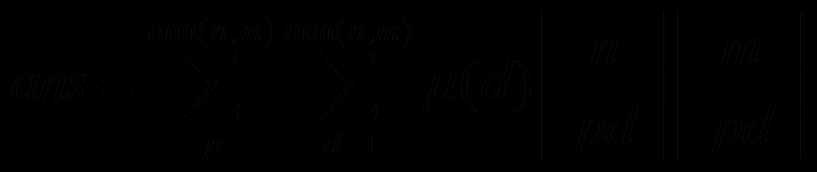
我们令![]() ,可得
,可得

直接算肯定要TLE,我们注意到前边部分也是可以类分块去搞的
后边的那个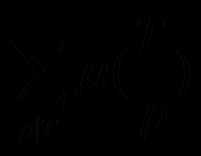 可以再看成一个函数,我们预处理出T所有取值的函数值来,就可以利用前缀和O(√n)得出块内答案了
可以再看成一个函数,我们预处理出T所有取值的函数值来,就可以利用前缀和O(√n)得出块内答案了
只需要暴力枚举每一个质数,去更新这个质数的倍数即可。
每个质数更新时均摊是O(nlogn)的,而质数个数恰好为O(n/logn),所以暴力枚举+处理前缀和时间复杂度是O(n)的
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define N 10000100
#define LL long long
int t,n,m;
int mu[N],notprime[N],prime[N];
LL sum[N];
int cun[N];
void getmu(){
mu[1]=1;notprime[1]=1;
pos(i,2,N-10){
if(!notprime[i]){
mu[i]=-1;
prime[++prime[0]]=i;
}
for(int j=1;j<=prime[0]&&prime[j]*i<=N-10;j++){
notprime[i*prime[j]]=1;
if(i%prime[j]==0){
mu[i*prime[j]]=0;break;
}
mu[i*prime[j]]=-mu[i];
}
}
pos(i,1,prime[0]){
for(int j=1;prime[i]*j<=N-10;j++){
cun[prime[i]*j]+=mu[j];
}
}
pos(i,1,N-10) sum[i]=sum[i-1]+cun[i];
}
LL getans(){
if(n>m) swap(n,m);
int last(0);LL ans(0);
for(int i=1;i<=n;i=last+1){
last=min(n/(n/i),m/(m/i));
ans+=(n/i)*1ll*(m/i)*1ll*(sum[last]-sum[i-1]);
}
return ans;
}
int main(){
scanf("%d",&t);
getmu();
while(t--){
scanf("%d%d",&n,&m);
printf("%lld\n",getans());
}
return 0;
}
标签:log src long 2-2 bsp 不同 http name amp
原文地址:http://www.cnblogs.com/Hallmeow/p/7994987.html