标签:一个 暴力 center 多少 printf 程序 tin 矩形 左右
纹波星(stripe)
【题目描述】
Kirby最近要去Ripple Star拜访Ribbon。但是他觉得空手去不太好,所以他决定带一点小礼物。
Kirby有n种颜色的缎带,每种颜色的缎带有ai条,Kirby希望用上所有的缎带来接成一长条来送给Ribbon。为了美观,长条中相邻的两段的颜色不能相同。驾驶Warp Star到达Ripple Star的路程很漫长,闲得无聊的Kirby想算一算他用这些缎带能接出多少不同的长条呢?作为Warp Star上的计算程序的你需要注意的是,Kirby可能还要在长条的一端接上一些小玩意,所以长条是有左右端之分的。
【输入数据】
第一行一个正整数n。
第二行n个正整数a1~an,表示各颜色缎带的数量。
【输出数据】
输出只有一行,一个整数表示答案。答案对1000000007取模。
【样例输入】
3
1 2 2
【样例输出】
12
【数据范围】
对于20%的数据,n=2;
对于50%的数据,n<=5;
另外20%的数据,ai均相同;
对于100%的数据,1<=n<=15,1<=ai<=5。
【样例解释】
“12323”,“13232”,“21323”,“31232”,“23123”,“23132”,“32123”,“32132”,“23213”,“32312”,“23231”,“32321”,共12种。
题意:给长度为Σai的数列染上n种颜色,每种颜色正好染ai段,相邻段不能染成同色,求方案数。
我们考虑状压,f[i][S][k]表示染了i段,每种颜色剩下的段数状态为S,第i+1段颜色为k的方案数。
显然,f[0][0][x]=1(1<=x<=15)
如何转移?我们枚举第i段染什么颜色(不能与i+1段的重复),f[i][S][i+1段的颜色]+=f[i-1][S‘][你当前枚举的颜色]。(这个位置填你当前枚举的颜色)
这样看起来复杂度是n*Σai*ai^n的。但是我们会发现,有一些状态根本不合法,即i必须=Σ剩余的段数。这些状态根本就不会也不能被搜索到。
但是,如果是普通的DP,这些状态很难不被搜索到(至少代码要写很长)。但是记搜可以很好的处理这一点。
我们可以发现i是不用记录的,只要每种颜色剩下的段数都为0,就是DP的边界。
则时间复杂度为n*n*ai^n。
考虑优化。(为了便于说明,i为上面的i)
考虑更改状态的表示,f[k][S]状态S表示每种段数剩下的颜色数有多少种,k表示当前DP做到的最后一段+1(i+1)的颜色的剩余段数。
为了简单起见,我们把状态改成f[k][a1][a2][a3][a4][a5](a1为段数为1的剩下的颜色数有多少种......)
显然,它是可以像上面一样转移的。
我们枚举第i段染的颜色的剩余段数(以剩余段数为3为例)(可以与i+1段的颜色的剩余段数重复)。
(1)与i+1段重复:f[i+1段的颜色的剩余段数][a1][a2][a3][a4][a5]=f[a3-1][a1][a2+1][a3-1][a4][a5]*(a3-1)(即剩余段数为3的其中一种颜色是和i+1段的颜色一致的,扣除,剩余段数为3的其它颜色这个位置都可以填)
(2)不与i+1段重复:f[i+1段的颜色的剩余段数][a1][a2][a3][a4][a5]=f[a3-1][a1][a2+1][a3-1][a4][a5]*a3(即剩余段数为3的颜色这个位置都可以填)
同样的,f[x][0][0][0][0][0]=1。
这样,时间复杂度就降为ai*ai*n^ai。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; long long mod=1000000007ll; long long dp[6][16][16][16][16][16]; int s[6];int n; long long DP(int k,int a[6]) { if(a[0]==n)return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=1; if(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]!=-1)return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]; dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=0; for(int i=1;i<=5;i++) { if(a[i]==0||(k==i&&a[i]==1))continue; a[i]--;a[i-1]++;long long y=DP(i-1,a);a[i]++;a[i-1]--; if(k==i)dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]+y*(a[i]-1))%mod; else dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]=(dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]+y*a[i])%mod; } return dp[k][a[1]][a[2]][a[3]][a[4]][a[5]]; } int main() { freopen("stripe.in","r",stdin);freopen("stripe.out","w",stdout); memset(dp,-1,sizeof(dp)); scanf("%d",&n); for(int i=1;i<=n;i++) { int b;scanf("%d",&b);s[b]++; } printf("%lld",DP(0,s)); return 0; }
切课本上瘾综合征(textbook)
【题目描述】
众所周知,小Z喜欢切课本,而且是上瘾的那种。
这一天,小G弄来了一本长为N,宽为M的课本请小Z来切。小G想让小Z用P-1刀把课本正好切为P个面积相等的矩形,而且每一刀必须把某一块课本切成两块。小Z自然很高兴,但小G还提出了一个要求,就是要使得这P个矩形中,长和宽比值的最大值最小。这让小Z有些犯难,他希望你能帮帮他,让他痛痛快快地切一次课本。
【输入数据】
输入一行三个正整数N,M,P,表示课本的长、宽和切出的矩形个数。
【输出数据】
输出一行一个浮点数,表示最小的长宽最大比值,当你的输出和标准答案不超过10^-6时,你的答案被视为正确答案。
【样例输入】
5 4 4
【样例输出】
1.250000000
【数据范围】
对于10%的数据,P=2;
对于30%的数据,P<=10;
对于60%的数据,P<=15;
另外10%的数据,M | N且P | (N/M);
对于100%的数据,1<=M<=N<=10000,1<=P<=20。
【样例解释】

先考虑暴力搜索。对于一块长为a,宽为b的矩形,切p刀。
我们把这个矩形分成两个小矩形,其中一个切p1刀,另一个切p2刀。(枚举p1,p2=p-p1)
考虑横着分成两个矩形和竖着分成两个矩形。
竖着切:显然两个小矩形的长之比为p1:p2。
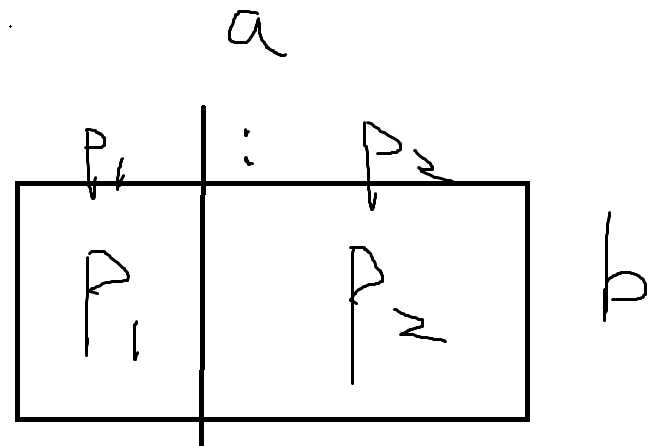
横着切同理:宽之比为p1:p2。
但是这样会TLE。我们会发现,这里面有很多相同状态。
考虑记搜。用f[i][j][k]表示当前对于一个长为j,宽为k的矩形切i刀,长宽比的最小值。
但是j是double,k也是double,怎么存到数组里。
map!把这两个double压成一个int。即变为f[i][S](S为map<j,k>)。
这样就可以记搜了。但是map真是慢,不开O2就T飞了。

#include<iostream> #include<cstdio> #include<map> #include<cstring> using namespace std; typedef pair<double,double> P; map<P,int> mp; double f[21][1000000],tot=0; double Get(double a,double b,int p) { if(a<b)swap(a,b);int now; if(!mp[P(a,b)]){mp[P(a,b)]=++tot;now=tot;} else now=mp[P(a,b)]; if(f[p][now])return f[p][now]; if(p==1)return f[p][now]=a/b; double ans1,ans2,ans=999999999; for(int p1=1;p1+p1<=p;p1++) { int p2=p-p1; ans1=max(Get(a/p*p1,b,p1),Get(a/p*p2,b,p2)); ans2=max(Get(a,b/p*p1,p1),Get(a,b/p*p2,p2)); ans=min(ans,min(ans1,ans2)); } return f[p][now]=ans; } int main() { freopen("textbook.in","r",stdin);freopen("textbook.out","w",stdout); int n,m,p;scanf("%d%d%d",&n,&m,&p); printf("%.15lf",Get((double)n,(double)m,p));cout<<" "<<tot; return 0; }
标签:一个 暴力 center 多少 printf 程序 tin 矩形 左右
原文地址:http://www.cnblogs.com/lher/p/8011557.html