标签:表示 表达式 多边形 变形 半径 等于 多边形面积 资料 ++i
多边形通常分为凸多边形和凹多边形
计算多边形面积有几种好用的算法
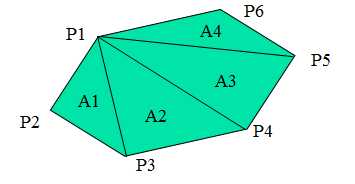
其核心思想都是把一个n(n>=3)边形转化为n-2个三角形,然后计算
一:海伦公式
最常见的多边形面积计算公式
此公式表达式为:
S= sqrt( p*(p-a)*(p-b)*(p-c))
其中p为此三角形的半周长,而a,b,c为三角形三边长
若三角形三点为x1,y1,x2,y2,x3,y3,
即p=(a+b+c)/2
a=sqrt((x2-x1)2+(y2-y1)2)
b=sqrt((x3-x2)2+(y3-y2)2)
c=sqrt((x3-x1)2+(y3-y1)2)
可能海伦公式就是 的一个变形而已。。。所以觉得意义也是等价的。。。
、
然后,我们再来进一步思考,这个东西和内心的关系:
对三角形的内切圆来说,如前面 白如冰所说会很自然联想到内切圆:
如此,我们发现,内切圆的半径实际上可以被 半周长 和 a,b,c表示了。
缺点:适用于边数很小的情况,一旦边数增多,计算繁琐,损失精度
C++代码:
1 typedef struct 2 { 3 int x; 4 int y; 5 }Point; 6 Point point[N]; 7 int Area(point[a],point[b],point[c]) 8 { 9 double area; 10 double la,lb,lc; 11 la=sqrt((point[b].x-point[a].x)*(point[b].y-point[a].y)); 12 lb=sqrt((point[c].x-point[b].x)*(point[c].y-point[b].y)); 13 lb=sqrt((point[c].x-point[a].x)*(point[c].y-point[a].y)); 14 p=(la+lb+lc)/2; 15 area=sqrt(p*(p-la)*(p-lb)*(p-lc)); 16 return area; 17 }
二:向量计算法
此方法可查看此资料:
https://files.cnblogs.com/files/tenjl-exv/%E5%A4%9A%E8%BE%B9%E5%BD%A2%E9%9D%A2%E7%A7%AF.ppt
有关资料证明:
我们都知道已知A(x1,y1)、B(x2,y2)、C(x3,y3)三点的面积公式为
|x1 x2 x3|
S(A,B,C) = |y1 y2 y3| * 0.5 = [(x1-x3)*(y2-y3) - (x2-x3)*(y1-y3)] /2
|1 1 1 |
(当三点为逆时针时为正,顺时针则为负的)
对于多边形A1A2A3、、、An(顺或逆时针都可以)
设平面上有任意的一点P,则有:
S(A1,A2,A3,、、、,An) = abs(S(P,A1,A2) + S(P,A2,A3)+、、、+S(P,An,A1))
P可以任意取点
如果P取多边形外一点,且取(0,0)时
设点顺序 (x1 y1) (x2 y2) ... (xn yn),则面积等于
|x1 y1| |x2 y2| |xn yn|
S= abs( | | + | | + ...... + | | ) /2
|x2 y2| |x3 y3| |x1 y1|
其中
|x1 y1|
| | === x1*y2 - y1*x2
|x2 y2|
因此面积公式展开为:
|x1 y1| |x2 y2| |xn yn|
S=abs( | | + | | + ...... + | | ) = abs(x1*y2-y1*x2+x2*y3-y2*x3+...+xn*y1-yn*x1) /2
|x2 y2| |x3 y3| |x1 y1|
C++代码如下:
int x[100]; int y[100]; double Area(int *x,int *y,int n) { double s=0; for(int i=0;i<n;i++) { int j=(i+1)%n; s+=x[i]*y[j]; s-=x[j]*y[i]; } s/=2; return (s>0?s:-s); } // area=Area(x,y,n); // n为点的个数
标签:表示 表达式 多边形 变形 半径 等于 多边形面积 资料 ++i
原文地址:http://www.cnblogs.com/tenjl-exv/p/8011513.html