标签:失败 存储 array 串匹配 i++ ges 数据结构 算法 空间
现在计算机处理涉及到大量的字符串操作,字符串的匹配是使用频率最高的字符串操作之一,大学数据结构与算法中字符串一章,也专门介绍了字符串匹配。
字符串的单模式匹配中最基础的算法是朴素的模式串匹配算法,比这更高级的是KMP算法。
/**
* 朴素的字符串模式匹配算法
* @param text 主串
* @param pattern 模式串
* @param pos 从主串中的pos位置开始匹配,pos>=0
* @return 模式串在主串中第一次出现的位置,-1代表没有匹配
*/
public static int indexOfPatternString(String text, String pattern, int pos){
int i = pos, j = 0;
char[] textChar = text.toCharArray();
char[] patternChar = pattern.toCharArray();
while(i < text.length() && j < pattern.length()){
if(textChar[i] == patternChar[j]){
i++;
j++;
}else{
i = i - j + 1;
j = 0;
}
}
if(j >= pattern.length())
return i - pattern.length() ;
return -1;
}
算法中i,j分别指示主串text和模式串pattern中当前正待比较的字符位置。算法的基本思想是:从主串text的pos位置的第一个字符比较,若相等,则继续逐个比较后续的字符;否则从主串的下一个字符起再重新和模式串比较。直至匹配成功或失败。下图是模式串‘abcac’和主串‘ababcabcacbab’的匹配过程。

KMP算法是由Knuth,Morris,Pratt共同提出的模式匹配算法,对于任何模式和目标序列,都可以在O(n+m)的时间数量级上完成串的匹配操作。其改进在于:每一趟匹配过程中出现字符比较不相等时,不需要回溯指针i,而是利用利用已经得到的“部分匹配”结果将模式向右滑动极可能远的一段距离后,继续进行比较。下面从具体的示例看起。上图的第三趟匹配中当i=7,j=5字符比较不等时,又从i=4,j=1重新开始比较,然后仔细观察后发现在i=4,j=1;i=5,j=1;i=6,j=1这三次比较都是不必要进行的,因为从第三趟部分匹配结果就可以得出,主串中第一个字符是a,因此无需在和这3个字符比较,而仅需将模式向右滑动3个字符的位置继续进行i=7,j=2时的字符比较即可。比较过程如下图所示
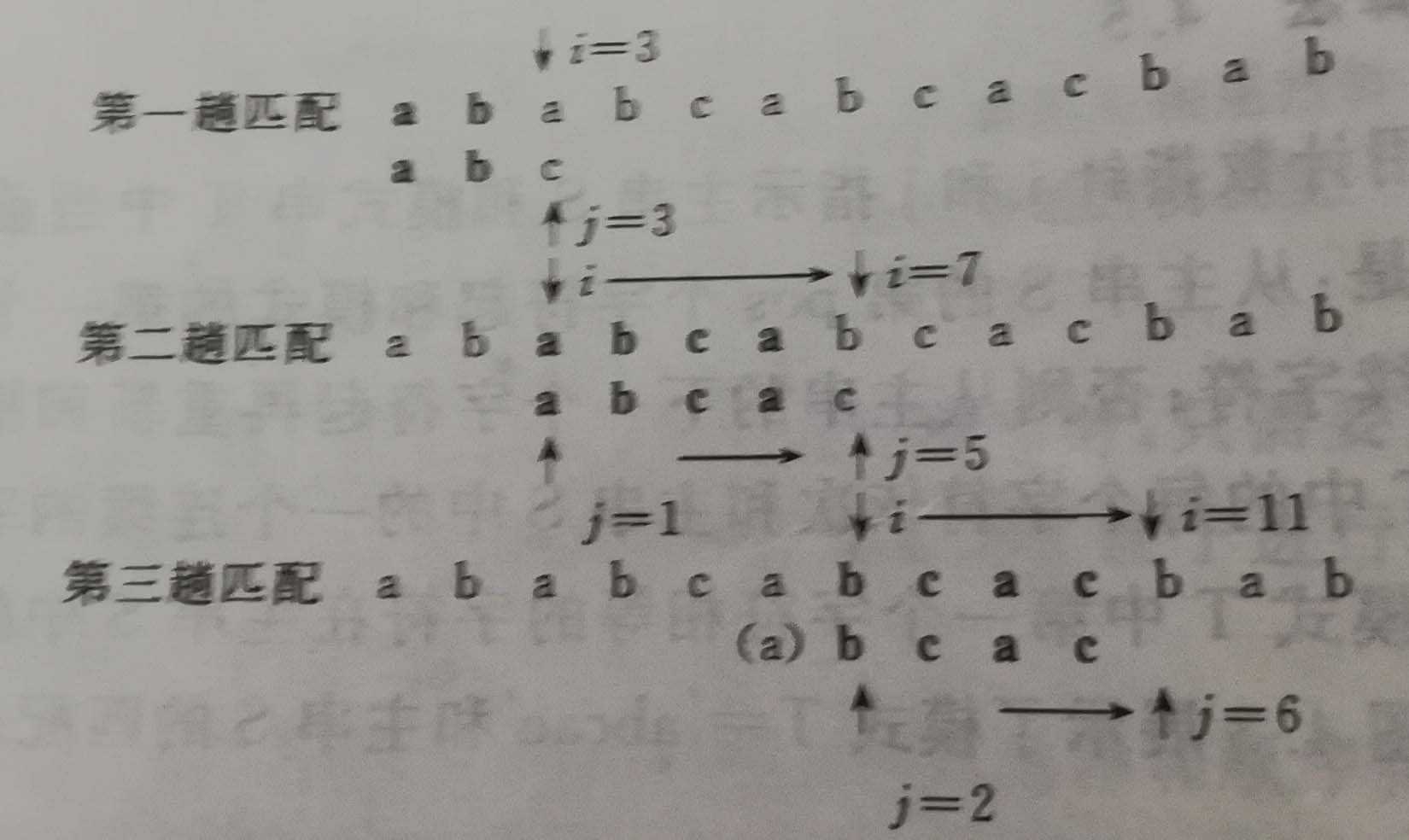
下面粘贴上严蔚敏和吴伟民的数据结构教程中对KMP算法的描述



该算法描述和代码是基于C语言的,串的起始下标从1开始,0位置存储串的长度,而本文给出java语言版的KMP算法,串的下标从0开始,当基本原理是一样的。
/**
* next数组初始化
* @param pattern 模式串
*/
private void initNext(String pattern){
int length = pattern.length();
next = new int[length+1];//浪费一个空间,但减少了i跟length的比较
char[] patternChar = pattern.toCharArray();
int i = 0, j = -1;
next[0] = -1;
while(i < length){
if(j == -1 || patternChar[i] == patternChar[j]){
i++;
j++;
next[i] = j;
}else
j = next[j];
}
}
/**
* 改进的next数组初始化
* @param pattern
*/
private void initProNext(String pattern){
int length = pattern.length();
next = new int[length+1];
char[] patternChar = pattern.toCharArray();
int i = 0, j = -1;
next[0] = -1;
while(i < length){
if(j == -1 || patternChar[i] == patternChar[j]){
i++;
j++;
if((i < length) && (patternChar[i] != patternChar[j]))
next[i] = j;
else
next[i] = next[j];
}else
j = next[j];
}
}
/**
* KMP算法主程序
* @param text
* @param pattern
* @param pos
* @return
*/
public int Index_KMP(String text, String pattern, int pos){
if(next == null)
initProNext(pattern);
int i = pos, j = 0;
char[] textChar = text.toCharArray();
char[] patternChar = pattern.toCharArray();
while(i < text.length() && j < pattern.length()){
if(j == -1 || textChar[i] == patternChar[j]){
i++;
j++;
}else{
j = next[j];
}
}
if(j >= pattern.length())
return i - pattern.length();
return -1;
}
KMP算法中包含了几个重要的概念,而书中并没有提及:前缀,非前缀,前缀自包含,建议参考这篇文章KMP算法详解
标签:失败 存储 array 串匹配 i++ ges 数据结构 算法 空间
原文地址:http://www.cnblogs.com/51zone/p/8012219.html