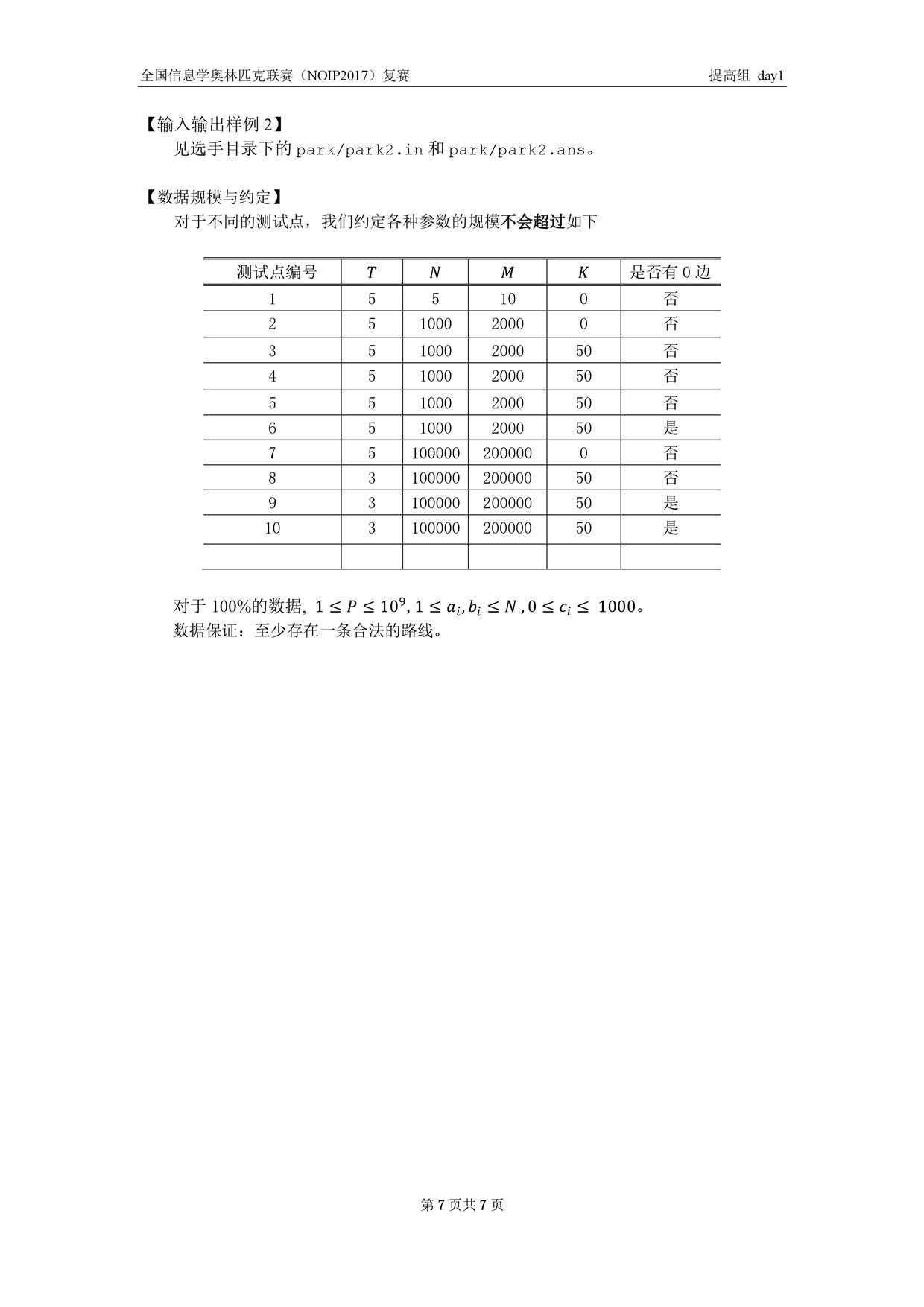
标签:div close using 技术分享 oid event mem 一个 --

考试的时候灵光一闪,瞬间推出DP方程,但是不知道怎么判-1,然后?然后就炸了。
后来发现,我只要把拓扑和DP分开,中间加一个判断,就AC了,可惜。
看这道题,我们首先来想有哪些情况是-1:只要有零环在满足题目要求的路径上,那么这条路径就可以不停地走,于是就-1了。
如何判有没有零环呢?
机械化地两遍不同方向的SPFA,就知道某个点在不在最短路上,以此建一个最短路图,在最短路图上找零环。于是就拓扑啦。稍加判断就解决了整个题目最关键的-1。
接下来就是DP了,设f[i][j]表示走到i点,走过路程已经超过i点到n点最短路径长度j的方案数。假设我们知道u点的f[u][k],接下来我们会走到v。那么如果走的这条边正好是最短路上的边,f[v][k]+=f[u][k];否则,我们根据f[u][k]知道现在已走路程为dis[u]+k,走完这条边后,就是dis[u]+k+w[i],这些路程会超过v到n的最短路长度dis[u]+k+w[i]-dis[v]这么长,所以,f[v][dis[u]+k+w[i]-dis[v]]+=[u][k]。
大体就是这样,剩下一些小细节就看代码吧。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int MAXN=100000+10,MAXM=200000+10,MAXK=60+10,inf=0x3f3f3f3f; 4 int n,m,Mod,k,e,qe,beg[MAXN],qbeg[MAXN],dis1[MAXN],p[MAXN],dis2[MAXN],nex[MAXM],qnex[MAXM],w[MAXM],qw[MAXM],to[MAXM],qto[MAXM],Indegree[MAXN],f[MAXN][MAXK],cnt,topoorder[MAXN]; 5 inline void read(int &x) 6 { 7 int data=0,w=1; 8 char ch=0; 9 while(ch!=‘-‘&&(ch<‘0‘||ch>‘9‘))ch=getchar(); 10 if(ch==‘-‘)w=-1,ch=getchar(); 11 while(ch>=‘0‘&&ch<=‘9‘)data=(data<<3)+(data<<1)+(ch^‘0‘),ch=getchar(); 12 x=data*w; 13 } 14 inline void chksum(int &a,int b) 15 { 16 a+=b; 17 if(a>Mod)a-=Mod; 18 } 19 inline void insert(int x,int y,int z) 20 { 21 to[++e]=y; 22 nex[e]=beg[x]; 23 beg[x]=e; 24 w[e]=z; 25 qto[++qe]=x; 26 qnex[qe]=qbeg[y]; 27 qbeg[y]=qe; 28 qw[qe]=z; 29 } 30 inline void init() 31 { 32 e=0; 33 memset(beg,0,sizeof(beg)); 34 qe=0; 35 memset(qbeg,0,sizeof(qbeg)); 36 memset(f,0,sizeof(f)); 37 cnt=0; 38 memset(Indegree,0,sizeof(Indegree)); 39 } 40 inline void SPFA() 41 { 42 queue<int> q; 43 for(register int i=1;i<=n;++i)dis1[i]=inf,p[i]=0; 44 q.push(1); 45 p[1]=1; 46 dis1[1]=0; 47 while(!q.empty()) 48 { 49 int x=q.front(); 50 q.pop(); 51 p[x]=0; 52 for(register int i=beg[x];i;i=nex[i]) 53 if(dis1[to[i]]>dis1[x]+w[i]) 54 { 55 dis1[to[i]]=dis1[x]+w[i]; 56 if(!p[to[i]]) 57 { 58 p[to[i]]=1; 59 q.push(to[i]); 60 } 61 } 62 } 63 for(register int i=1;i<=n;++i)dis2[i]=inf,p[i]=0; 64 q.push(n); 65 p[n]=1; 66 dis2[n]=0; 67 while(!q.empty()) 68 { 69 int x=q.front(); 70 q.pop(); 71 p[x]=0; 72 for(register int i=qbeg[x];i;i=qnex[i]) 73 if(dis2[qto[i]]>dis2[x]+qw[i]) 74 { 75 dis2[qto[i]]=dis2[x]+qw[i]; 76 if(!p[qto[i]]) 77 { 78 p[qto[i]]=1; 79 q.push(qto[i]); 80 } 81 } 82 } 83 } 84 inline void toposort() 85 { 86 queue<int> q; 87 for(register int x=1;x<=n;++x) 88 for(register int i=beg[x];i;i=nex[i]) 89 if(dis1[to[i]]==dis1[x]+w[i])Indegree[to[i]]++; 90 for(register int i=1;i<=n;++i) 91 if(!Indegree[i])q.push(i),topoorder[++cnt]=i; 92 while(!q.empty()) 93 { 94 int x=q.front(); 95 q.pop(); 96 for(register int i=beg[x];i;i=nex[i]) 97 if(dis1[to[i]]==dis1[x]+w[i]) 98 { 99 Indegree[to[i]]--; 100 if(!Indegree[to[i]])q.push(to[i]),topoorder[++cnt]=to[i]; 101 } 102 } 103 } 104 inline void DP() 105 { 106 f[1][0]=1; 107 for(register int j=0;j<=k;++j) 108 { 109 for(register int p=1;p<=cnt;++p) 110 { 111 int x=topoorder[p]; 112 for(register int i=beg[x];i;i=nex[i]) 113 if(dis1[to[i]]==dis1[x]+w[i])chksum(f[to[i]][j],f[x][j]); 114 } 115 for(register int x=1;x<=n;++x) 116 for(register int i=beg[x];i;i=nex[i]) 117 if(dis1[to[i]]!=dis1[x]+w[i]&&j+dis1[x]+w[i]-dis1[to[i]]<=k)chksum(f[to[i]][j+dis1[x]+w[i]-dis1[to[i]]],f[x][j]); 118 } 119 } 120 int main() 121 { 122 freopen("park.in","r",stdin); 123 freopen("park.out","w",stdout); 124 int T; 125 read(T); 126 while(T--) 127 { 128 init(); 129 read(n);read(m);read(k);read(Mod); 130 int mark=0; 131 for(register int i=1;i<=m;++i) 132 { 133 int u,v,w; 134 read(u);read(v);read(w); 135 insert(u,v,w); 136 } 137 SPFA(); 138 toposort(); 139 for(register int i=1;i<=n;++i) 140 if(Indegree[i]&&dis1[i]+dis2[i]<=dis1[n]+k) 141 { 142 printf("-1\n"); 143 mark=1; 144 break; 145 } 146 if(mark)continue; 147 DP(); 148 int ans=0; 149 for(register int i=0;i<=k;++i)chksum(ans,f[n][i]); 150 printf("%d\n",ans); 151 } 152 return 0; 153 }
标签:div close using 技术分享 oid event mem 一个 --
原文地址:http://www.cnblogs.com/hongyj/p/8012509.html