FBI树(fbi)
链接:http://ybt.ssoier.cn:8088/problem_show.php?pid=1365时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
T的根结点为R,其类型与串S的类型相同;
若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2N的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
【输入】
第一行是一个整数N(0 <= N <= 10),第二行是一个长度为2N的“01”串。
【输出】
一行,这一行只包含一个字符串,即FBI树的后序遍历序列。
【输入样例】
3 10001011
【输出样例】
IBFBBBFIBFIIIFF
【提示】
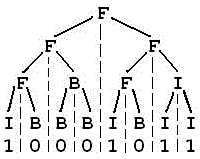
对于40%的数据,N <= 2;
对于100%的数据,N <= 10。
#include<iostream> #include<cstdio> #include<cstring> #include<vector> #include<algorithm> using namespace std; int p[1<<12]; int check(int a,int b) { if(a==1&&b==1)return 1; if(a==0&&b==0)return 0; return 2; } void chan(int a) { switch(a) { case 1:printf("I");break; case 0:printf("B");break; case 2:printf("F");break; } } void reck(int d,int ed) { if(!d)return ; for(int i=ed-d;i<ed;i++) p[i]=check(p[i*2],p[i*2+1]); reck(d/2,ed-d); } void print(int t) { if(p[t]==-1)return ; print(t*2); print(t*2+1); chan(p[t]); } int main() { int n; cin>>n; int t=1<<(n+1),m=1<<n;; t-=1; string s; cin>>s; memset(p,-1,sizeof(p)); for(int i=t-m+1;i<=t;i++) p[i]=s[i-(t-m+1)]-‘0‘; reck(m/2,t-m+1); print(1); cout<<endl; }
