标签:style blog http color io ar 2014 div art
拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)是
1979年苏联物理学家拉比诺维奇和法布里康特提出模拟非平衡介
质自激波动的非线性常微分方程组:
dot{x} = y (z - 1 + x^2) + \gamma x
dot{y} = x (3z + 1 - x^2) + \gamma y
dot{z} = -2z (\alpha + xy)
其中 α, γ 是控制系统的参数.
Danca and Chen指出由于拉比诺维奇-法布里康特方程包含平方项,
因此比较难以分析,即便选择的参数相同,但由于求解微分方程
组的步骤的不同也会导致不同的吸引子。
参数值:α=1.1,γ=0.803..0.917,t=0...130
初始条件:x(0)=-1,y(0)=0,z(0)=0.5
在t<20时,系统表现为自激振动,当t>20,系统进入馄饨态。
相关软件:混沌数学及其软件模拟
相关代码:
class RabinovichFabrikantEquation : public DifferentialEquation { public: RabinovichFabrikantEquation() { m_StartX = -1.0f; m_StartY = 0.0f; m_StartZ = 0.5f; m_ParamA = 1.1f; m_ParamB = 0.87f; m_StepT = 0.002f; } void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ) { dX = y*(z - 1 + x*x) + m_ParamB*x; dY = x*(3*z + 1 - x*x) + m_ParamB*y; dZ = -2*z*(m_ParamA + x*y); } bool IsValidParamA() const {return true;} bool IsValidParamB() const {return true;} };
相关截图:


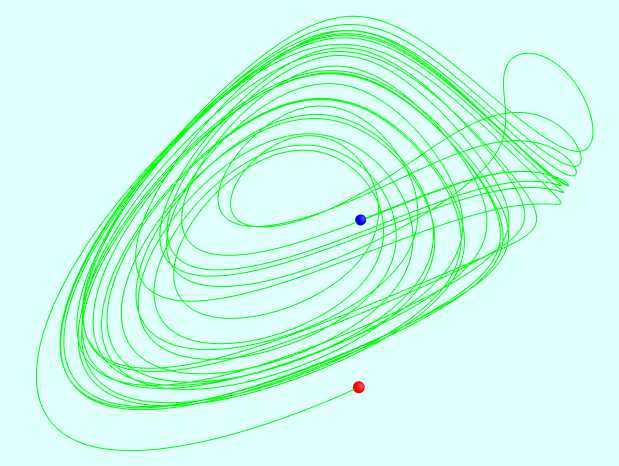
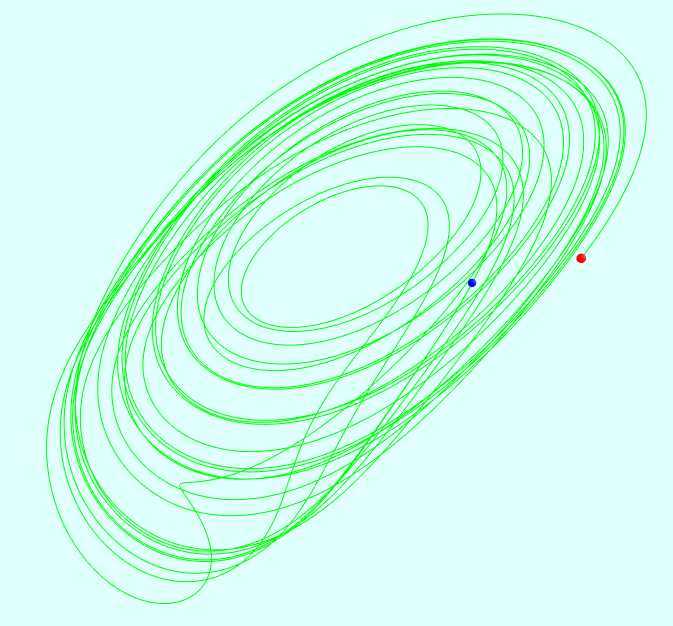
混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)
标签:style blog http color io ar 2014 div art
原文地址:http://www.cnblogs.com/WhyEngine/p/3974361.html