标签:style blog http color io ar 2014 div art
蔡氏电路(英语:Chua‘s circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为。
在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1]。这个电路的制作容易程度使
它成为了一个无处不在的现实世界的混沌系统的例子,导致一些人声明它是一个“混沌系统的典范”.
通过电磁学定律的应用,蔡氏电路可以被准确的建立数学模型:这是变量x(t), y(t),和z(t)的一个三个非线
性常微分方程的系统,分别是在电容C1和C2上的电压,和在电感L1上的电流强度。这些蔡氏方程有:
frac{dx}{dt} = a*[y-x-f(x)]
frac{dy}{dt} = x-y+z
frac{dz}{dt} = -b*y
函数 f(x) 描述了非线性电阻的电子响应,并且它的形状是依赖于它的元件的特定配置。
f(x)=cx(t)+0.5(d-c)(|x(t)+1|-|x(t)-1|)
参数 α 和 β 是由电路元件的特定值来决定的。
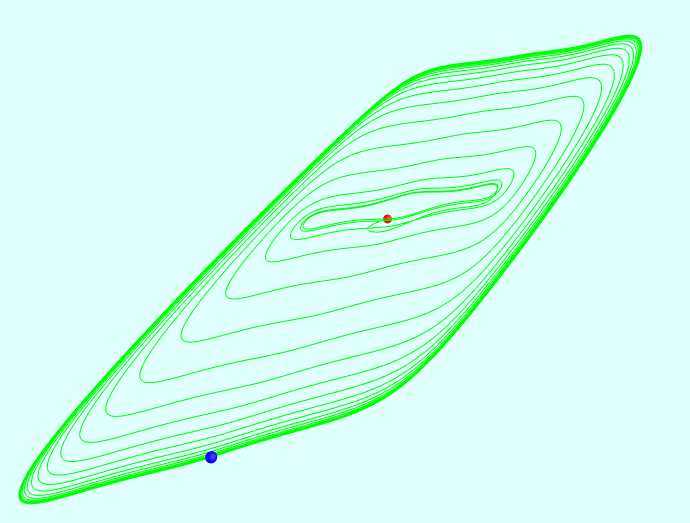
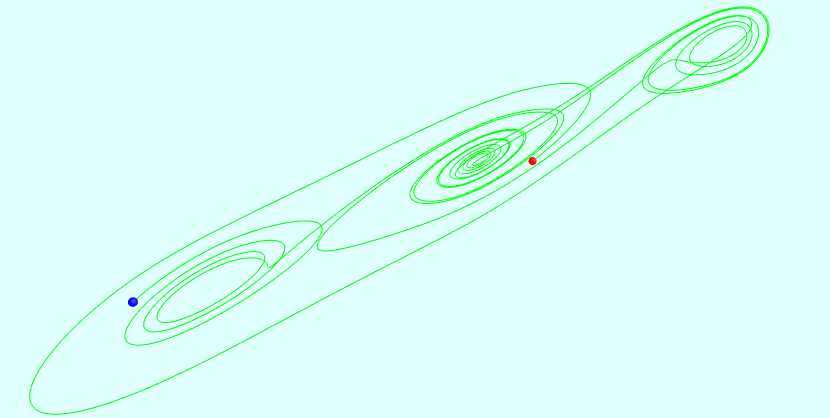
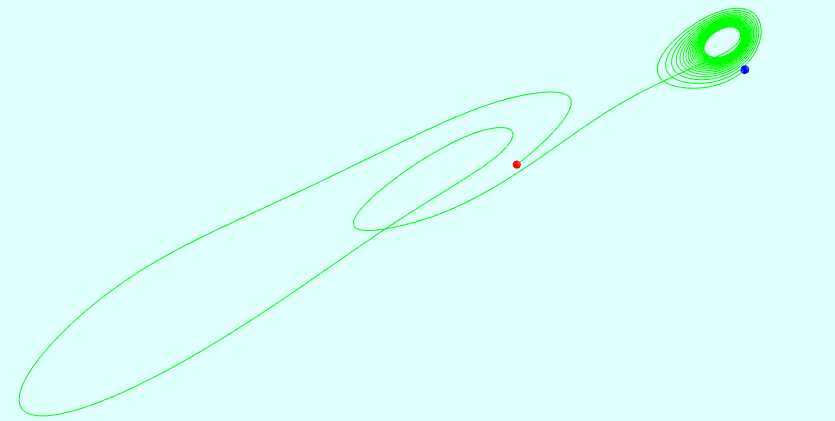
被称为双涡旋"The Double Scroll"的一个混沌吸引子,是因为它在(x,y,z)空间的形状, 被首次观察到在电子线路
中包含一个非线性元件,元件的f(x)是一个三段的线性函数
作为一个最简单的实验实现的电路,并且存在一种简单而准确的理论模型相结合,使蔡氏电路成为一个研究混沌
理论的许多基础研究和应用的问题的实用系统。正因为如此,它一直是许多研究的对象,并广泛被人们在文献中引用。
相关软件:混沌数学及其软件模拟
相关代码:
class ChuaCircuit : public DifferentialEquation { public: ChuaCircuit() { m_StartX = 0.1f; m_StartY = 0.3f; m_StartZ = -0.6f; m_ParamA = 3.0f; m_ParamB = 1.0f; m_ParamC = 2.0f; m_ParamD = 0.5f; } void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ) { float f = m_ParamC*x + 0.5f*(m_ParamD-m_ParamC)*(fabsf(x+1)-fabsf(x-1)); dX = m_ParamA*(y - x - f); dY = x - y + z; dZ = -m_ParamB*y; } bool IsValidParamA() const {return true;} bool IsValidParamB() const {return true;} bool IsValidParamC() const {return true;} bool IsValidParamD() const {return true;} };
相关截图:
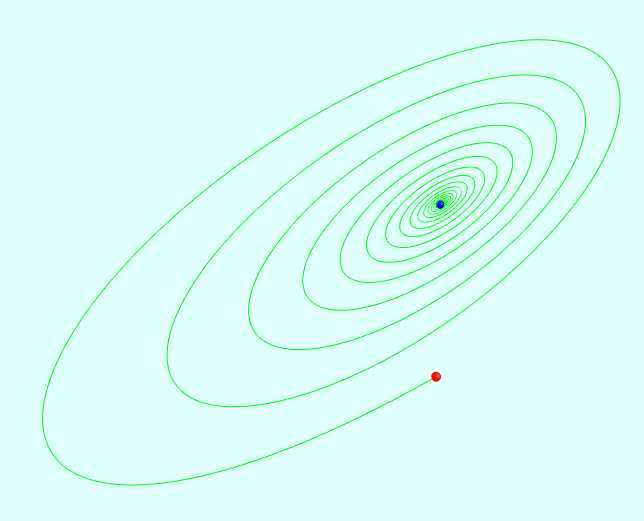
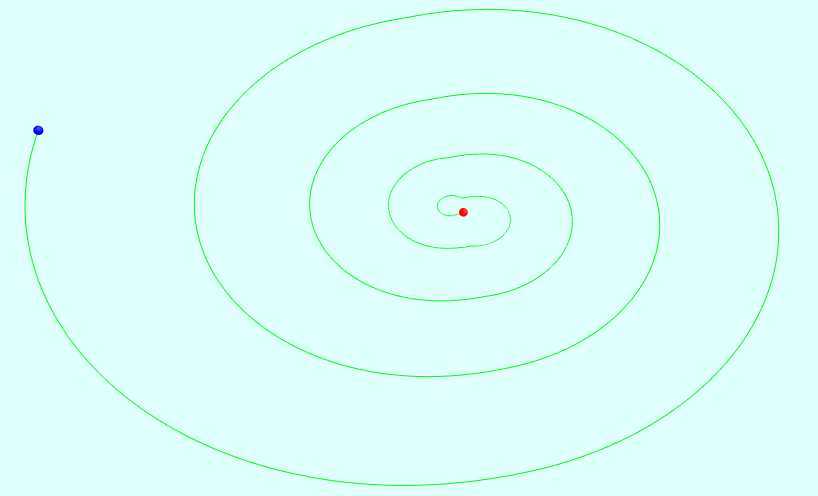
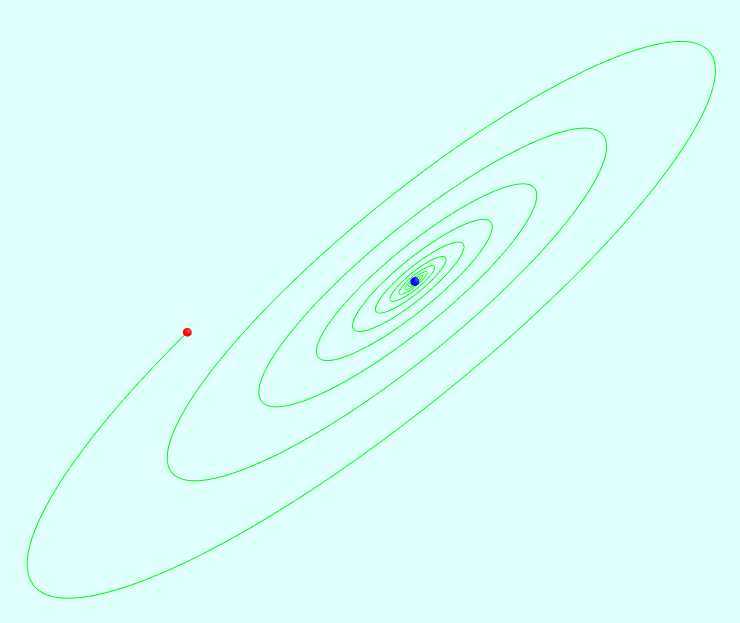
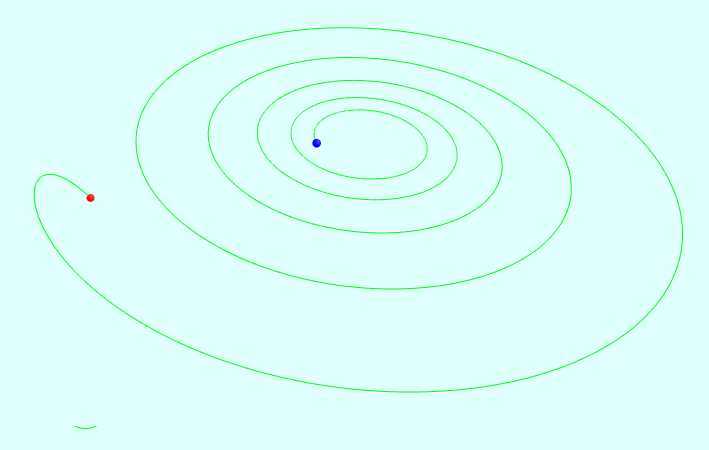
相关代码:
// http://wenku.baidu.com/view/a4b0df0bf78a6529647d5349.html class ChuaCircuit2 : public DifferentialEquation { public: ChuaCircuit2() { m_StartX = 0.1f; m_StartY = 0.3f; m_StartZ = -0.6f; m_ParamA = 12.8f; m_ParamB = 19.1f; m_ParamC = 0.45f; m_ParamD = -1.1f; m_ParamE = 0.6f; } void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ) { float h = m_ParamE*x + m_ParamD*x*fabs(x) + m_ParamC*x*x*x; dX = m_ParamA*(y - h); dY = x - y + z; dZ = -m_ParamB*y; } bool IsValidParamA() const {return true;} bool IsValidParamB() const {return true;} bool IsValidParamC() const {return true;} bool IsValidParamD() const {return true;} bool IsValidParamE() const {return true;} };
相关截图:

标签:style blog http color io ar 2014 div art
原文地址:http://www.cnblogs.com/WhyEngine/p/3974351.html