某变换好题。不过听说还有O(2^n*n^2)DP的……
Description
给定一个n*m的01矩阵,你可以选择对任意行和任意列取反,使得最终“1”的数量尽量少。
Input
第一行两个整数n,m。
接下来n行,每行m个字符,描述一个01矩阵。
Output
一个整数表示最少的1的数量。
Sample Input
3 4
0110
1010
0111
Sample Output
2
HINT
1 <= n <= 20,1 <= m <= 100000。
Solution
首先发现矩阵只有20行,经过一番脑补,可以把这二十行压成一个数。
然后我们就得到了m个数。
然后在行上的取反就相当于将这m个数同时异或上同一个数。
然后我们要求的就是,找出一个数,使得这m个数同时异或上这个数后,每个数的二进制位中的0和1的个数的最小值总和最小。
我们设ans[x]为当异或的数为x时的答案,a数组用来存放m个数,d[x]为x的二进制位中0和1的个数的最小值。
所以:
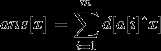 ,
,
我们稍微改一改,用w[x]表示在m个数中,为x的数有多少个:
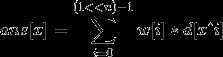 。
。
等等,是不是发现了什么?这不就是卷积FWT的式子吗?
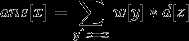 。
。
时间复杂度O(nm+2^n*n)。
#include <cstdio> #include <cstring> #include <algorithm> #define ll long long #define MS 23 #define MN 100005 #define MM 1100005 using namespace std; char c[MS][MN]; int a[MN]; ll A[MM],B[MM],C[MM]; int n,m,ans; inline int read() { int n=0,f=1; char c=getchar(); while (c<‘0‘ || c>‘9‘) {if(c==‘-‘)f=-1; c=getchar();} while (c>=‘0‘ && c<=‘9‘) {n=n*10+c-‘0‘; c=getchar();} return n*f; } void FWT(ll* a,int len,bool g) { register int wt,st,i; ll x,y; for (wt=1;wt<len;wt<<=1) for (st=0;st<len;st+=wt<<1) for (i=0;i<wt;++i) { x=a[st+i]; y=a[st+wt+i]; a[st+i]=x+y; a[st+wt+i]=x-y; if (g) a[st+i]>>=1,a[st+wt+i]>>=1; } } int main() { register int i,j; n=read(); m=read(); ans=n*m; for (i=0;i<n;++i) scanf("%s",c[i]+1); for (i=n-1;i>=0;--i) for (j=1;j<=m;++j) a[j]=(a[j]<<1)+c[i][j]-‘0‘; for (i=1;i<=m;++i) ++A[a[i]]; for (i=0;i<(1<<n);++i) B[i]=B[i>>1]+(i&1); for (i=0;i<(1<<n);++i) B[i]=min(B[i],n-B[i]); FWT(A,1<<n,false); FWT(B,1<<n,false); for (i=0;i<(1<<n);++i) C[i]=A[i]*B[i]; FWT(C,1<<n,true); for (i=0;i<(1<<n);++i) ans=min(ans,(int)C[i]); printf("%d",ans); }
Last Word
如果把FWT中的if语句改成(x+y)/g,(x-y)/g,效率会慢5倍,除法真是个可怕的东西。
