支持向量机 (3)

线性可分问题的支持向量机学习方法，对线性不可分训练数据是不适用的，因为这时上述方法中的不等式约束并不能都成立，因此这时候需要将硬间隔最大化，使其变成软间隔最大化。

假定给定特征空间上的训练数据集：T={(x₁,y₁),(x₂,y₂),...(x_n,y_n)}，x_i为第i个特征向量，y_i为x_i的类标记，一般情况下，线性不可分的数据主要在于存在部分特异点，除去这些点后剩下的大部分样本点组成的集合是线性可分的。线性不可分意味着样本点(x_i,y_i)不能满足函数间隔大于等于1的约束条件，为了解决这个问题，可以对样本点(x_i,y_i)引进松弛变量ξ_i≥0，使得函数间隔加上松弛变量ξ_i大于等于1，这样约束条件则变为：

同时，对于每个松弛变量ξ_i，支付一个代价ξ_i，目标由原来的变成,这里C>0称为惩罚函数，一般由实际问题的情况来变动C的值，当C值增大的时候对误分类的惩罚增大，C值小的时候对误分类的惩罚减小，最小化目标函数包含两层含义：使尽量小即使间隔尽量大，同时使误分类点的个数尽量小，C是作为调和二者的系数。

线性不可分的线性支持向量机的学习问题转变为如下凸二次规划问题：

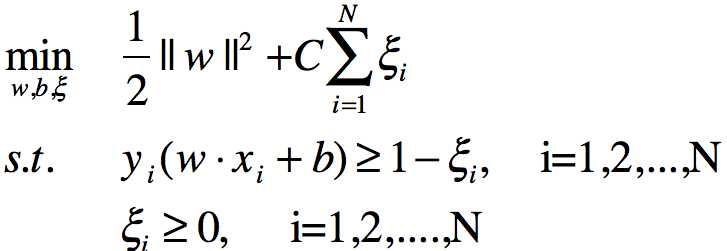
上述问题是一个凸二次规划问题，因而关于(w,b,ξ)的解是存在的，可以证明w的解是唯一的，但b的解可能不唯一，而是存在于一个区间。

由上式得到的解w，b，可以得到分离超平面wx+b=0及分类决策函数 f(x)=sign(wx+b)  ，称这样的模型为训练样本线性不可分时的线性支持向量机，简称线性支持向量机。