原题
求树上距离不超过k的点对数。
树分治的板子题。
每次把一棵树由重心分为多颗树,分别递归处理。
我们要求的就是不在同一个联通块中的符合答案的对数(在同一个的会通过递归转化为不在同一个的)。
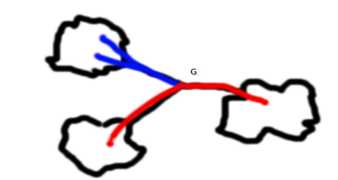
每次处理重心到每个点的dis,然后用two-points求出距离小于等于k的点对数。然而这不是最终答案,因为这可能包含了在同一棵子树内的情况,如图(红色为所求,蓝色为多余)。所以我们还要再减去子树的该情况才是答案。
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 10010
typedef long long ll;
int n,k,f[N],sze[N],dis[N],cnt,head[N],son[N];
bool vis[N];
ll ans;
struct hhh
{
int to,w,next;
}edge[2*N];
int read()
{
int ans=0,fu=1;
char j=getchar();
for (;(j<'0' || j>'9') && j!='-';j=getchar()) ;
if (j=='-') j=getchar(),fu=-1;
for (;j>='0' && j<='9';j=getchar()) ans*=10,ans+=j-'0';
return ans*fu;
}
void add(int u,int v,int w)
{
edge[cnt].to=v;
edge[cnt].next=head[u];
edge[cnt].w=w;
head[u]=cnt++;
}
int calcG(int x)
{
static int qn,q[N];
int u,v,mx=n,G;
q[qn=1]=x;
f[x]=0;
for (int ql=1;ql<=qn;ql++)
{
sze[u=q[ql]]=1;
son[u]=0;
for (int i=head[u];i;i=edge[i].next)
if (vis[v=edge[i].to] || v==f[u]) continue;
else f[v]=u,q[++qn]=v;
}
for (int ql=qn;ql>=1;ql--)
{
u=q[ql];
v=f[u];
son[u]=max(son[u],qn-sze[u]);
if (son[u]<mx) G=u,mx=son[u];
if (!v) break;
sze[v]+=sze[u];
if (sze[u]>son[v]) son[v]=sze[u];
}
return G;
}
inline ll calc(int x,int L)
{
static int qn,q[N],d[N];
int u,v,d_n=0;
q[qn=1]=x;
dis[x]=L;
f[x]=0;
for (int ql=1;ql<=qn;ql++)
{
d[d_n++]=dis[u=q[ql]];
for (int i=head[u];i;i=edge[i].next)
if (vis[v=edge[i].to] || v==f[u]) continue;
else f[v]=u,dis[v]=dis[u]+edge[i].w,q[++qn]=v;
}
ll count=0;
sort(d,d+d_n);
int l=0,r=d_n-1;
while (l<r)
{
if (d[l]+d[r]<=k) count+=r-l++;
else --r;
}
return count;
}
void solve(int x)
{
int G=calcG(x);
vis[G]=1;
ans+=calc(G,0);
for (int i=head[G];i;i=edge[i].next)
if (!vis[edge[i].to]) ans-=calc(edge[i].to,edge[i].w);
for (int i=head[G];i;i=edge[i].next)
if (!vis[edge[i].to]) solve(edge[i].to);
}
int main()
{
while (~scanf("%d%d",&n,&k) && (n || k))
{
ans=0;
cnt=1;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
for (int i=1,u,v,w;i<n;i++)
{
u=read();v=read();w=read();
add(u,v,w);
add(v,u,w);
}
solve(1);
printf("%lld\n",ans);
}
return 0;
}