机器学习之数据清洗与特征提取

欢迎大家前往腾讯云社区，获取更多腾讯海量技术实践干货哦~

作者：汪毅雄

导语：本文详细的解释了机器学习中，经常会用到数据清洗与特征提取的方法PCA，从理论、数据、代码三个层次予以分析。

机器学习，这个名词大家都耳熟能详。虽然这个概念很早就被人提出来了，但是鉴于科技水平的落后，一直发展的比较缓慢。但是，近些年随着计算机硬件能力的大幅度提升，这一概念慢慢地回到我们的视野，而且发展速度之快令很多人刮目相看。尤其这两年，阿法狗在围棋届的神勇表现，给人在此领域有了巨大的遐想空间。

所谓机器学习，一般专业一点的描述其是：机器学习(Machine Learning, ML)是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

机器学习这门技术是多种技术的结合。而在这个结合体中，如何进行数据分析处理是个人认为最核心的内容。通常在机器学习中，我们指的数据分析是，从一大堆数据中，筛选出一些有意义的数据，推断出一个潜在的可能结论。得出这个不知道正确与否的结论，其经过的步骤通常是：

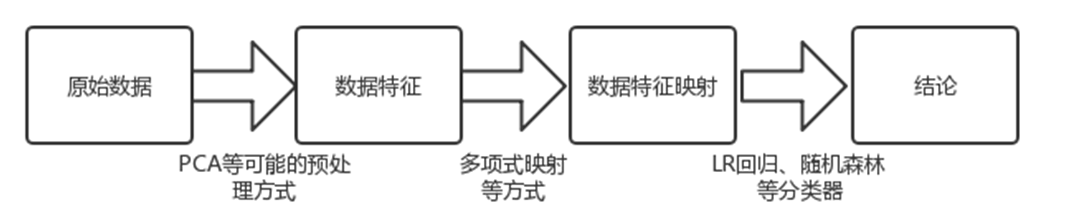
1、预处理：把数据处理成一些有意义的特征，这一步的目的主要是为了降维。

2、建模：这部分主要是建立模型（通常是曲线的拟合），为分类器搭建一个可能的边界。

3、分类器处理：根据模型把数据分类，并进行数据结论的预测。

本文讲的主要是数据的预处理（降维），而这里采用的方式是PCA。

PCA的个人理论分析：

假设有一个学生信息管理系统，里面需要存储人性别的字段，我们在数据库里可以有M、F两个字段，用1、0分别代表是、否。当是男学生的时候其中M列为1，F列为0，为女生时M列为0，F列为1。我们发现，对任意一条记录，当M为1，F必然为0，反之也是如此。因此实际过程，我们把M列或F列去掉也不会丢失任何信息，因为我们可以反推出结论。这种情况下的M、F列的关联比是最高的，是100%。

再举另外一个例子，小明开了家店铺，他每天在统计其店铺的访问量V和成交量D。可以发现，往往V多的时候，D通常也多。D少的时候，V通常也很少。可以猜到V和D是有种必然的联系，但又没有绝对的联系。此时小明如果想根据V、D来衡量这一天的价值，往往可以根据一些历史数据来计算出V、D的关联比。拍脑门说一个，如果关联比大于80%，那么可以取VD其中任意一个即可衡量当天价值。这样就达到了降维的效果。

当然降维并非只能在比如说2维数据[V，D]中选取其中的1维[V]作为特征值，它有可能是在V+D的情况下，使得对[V, D]的关联比最大。

但是PCA思想就是如此。简单点说：假设有x1、x2、x3…xn维数据，我们想把数据降到m维，我们可以根据这n维的历史数据，算出一个与x1…xn相关m维数据，使得这个m维数据对历史数据的关联比达到最大。

数学分析

假设我们有一组二维数据

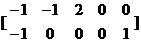
如果我们必须使用一维来表示这些数据，又希望尽量保留原始的信息，你要如何选择？

这个问题实际上是要在二维平面中选择一个方向，将所有数据都投影到这个方向所在直线上，用投影值表示原始记录。这是一个实际的二维降到一维的问题。

那么如何选择这个方向才能尽量保留最多的原始信息呢？一种直观的看法是：希望投影后的投影值尽可能分散，这样投影的范围越大，在做分类的时候也就更容易做分类器。

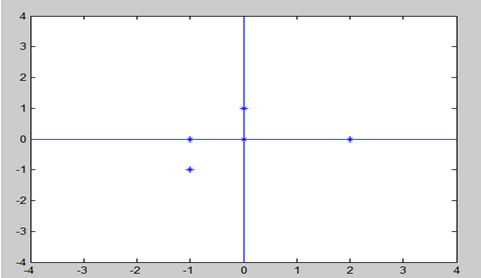
以上图为例，可以看出如果向x轴投影，那么最左边的两个点会重叠在一起，中间的两个点也会重叠在一起，于是本身四个各不相同的二维点投影后只剩下两个不同的值了，这是一种严重的信息丢失。同理，如果向y轴投影中间的三个点都会重叠，效果更糟。所以看来x和y轴都不是最好的投影选择。直观来看，如果向通过第一象限和第三象限的斜线投影，则五个点在投影后还是可以区分的。

我们希望投影后投影值尽可能分散，那什么是衡量分散程度的统计量呢，显然可以用数学上的方差来表述。

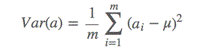
通常，为了方便计算，我们会把每个点都减去均值，这样得到的点的均值就会为0.这个过程叫做均一化。均一化后：

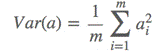
于是上面的问题被形式化表述为：寻找一个基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

我们跳出刚才的例子，因为很容易把刚才的结论推广到任意纬度。要求投影点的方差最大值所对应的基u，这时有两种方法来求解：

方法一：

假设有个投影A： 

显然刚才说的方差V可以用来表示：

而投影A = 原始数据X . U；

这样方差可以表示为：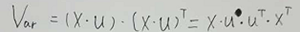 

求这个方差的最大值，我们可以用拉格朗日插值法来做

L（u，λ）为：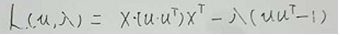 

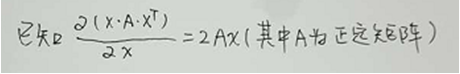
求导L’：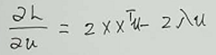 

令导数为0： 

这样问题就转换成求X.XT的特征值和特征向量，问题就迎刃而解了。

同时我们可以知道，特征值和特征向量有很多个，当λ最大的时候所对应的特征向量，我们把它叫作主成份向量。如果需要将m降维为n，只需要去前n大的特征值所对应的特征向量即可。

方法二：

对于上面二维降成一维的问题来说，找到那个使得方差最大的方向就可以了。不过对于更高维，首先我们希望找到一个方向（基）使得投影后方差最大，当我们找第二个方向（基）的时候，为了最大可能还原多的信息，我们显然不希望第二个方向与第一个方向有重复的信息。这个从向量的角度看，意味这一个向量在另一个向量的投影必须为0.

这就有：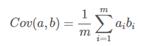

这时候我们思路就很明了：将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段本身的方差则尽可能大。

还是假设我们原始数据为A

我们做一个处理A.A^T得到：

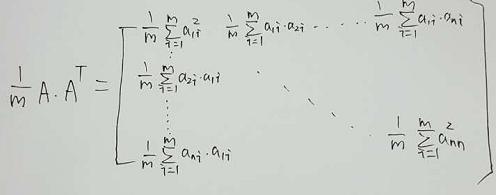
我们发现要是能找到一个基使得这个矩阵变成一个，除了斜对角外，其余全是0的话，那这个基就是我们需要的基。那么问题就转换成矩阵的对角化了。

先说一个先验知识：

在线性代数上，我们可以知道实对称矩阵不同特征值对应的特征向量必然正交。对一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1,e2,?,en。

组合成矩阵的形式如图：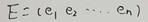

由上结论又有一个新的结论就是，对于实对称矩阵A，它的特征向量矩阵为E，必然满足：

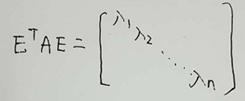
有了这个先验知识，我们假设原始数据A，基为U，投影后的数据为Y。则有Y=UA。根据上面所说的要是投影后的矩阵Y的Y.Y^T为一个对角阵，那么就有：

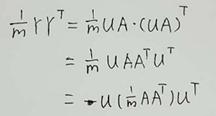
要是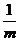Y.Y^T为对角阵，那么只需要U是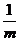A.A^T的特征向量即可，那么问题最终还是转换为求AA^T的特征向量。

代码实现：

刚才说了两种PCA的计算思路，我们简单看下代码的实现吧，由于matlab自带了求特征向量的函数，这边使用matlab进行模拟。

我们用测试数据试试：

当我们只保留0.5的成分时，newA从3维降到1维，当进行还原时，准确性也会稍微差些

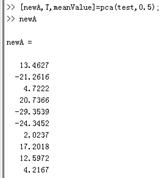
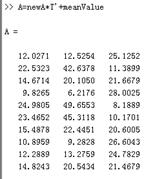
当我们保留0.9的成分时，newA从3维降到2维，当进行还原时，还原度会稍微好些。

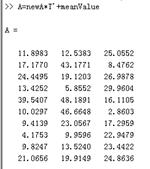
当我们保留0.97的成分时，就无法降维了。这时候就可以100%还原了。

总结一下：

我们在做机器学习的数据分析的时候，由于数据集的维度可能很高，这时候我们需要对数据进行降维。本文从各个方向介绍了一下降维的经典方法PCA，也从代码的角度告诉了怎么降维的过程。实际操作可能会比较简单，但是原理个人觉得还是有学习的地方的。

 相关阅读