单调队列是什么呢?可以直接从问题开始来展开。
Poj 2823
给定一个数列,从左至右输出每个长度为m的数列段内的最小数和最大数。
数列长度:\(N <=10^6 ,m<=N\)
解法①
很直观的一种解法,那就是从数列的开头,将窗放上去,然后找到这最开始的k个数的最大值,然后窗最后移一个单元,继续找到k个数中的最大值。

这种方法每求一个f(i),都要进行k-1次的比较,复杂度为$ O(Nk) $。
显然,如果暴力时间复杂度为 $ O(Nm) $ 不超时就怪了。
解法②
还有一种想法是维护一个BST,然后for循环从左到右,依次加入到BST里面,如果某个数超出了k的范围,就从BST中删除。
因为每个数只insert一次,最多erase一次,所以复杂度是\(O(NlogN)\)的,已经很不错了。
但是\(10^6\)级别的极限数据,这种做法会被卡掉的,况且维护一个BST的代码也比较麻烦。
void getans() {
BST tree;
for(int i=1,j=1;i<=N;++i) {
tree.insert(a[i]);
while(j<=i-k) {
tree.erase(a[j]);
--j;
}
cout<<tree.max()<<endl;
}
}解法③
我们知道,解法①在暴力枚举的过程中,有一个地方是重复比较了,就是在找当前的f(i)的时候,i的前面其它m-1个数在算f(i-1)的时候我们就比较过了。
当你一个个往下找时,每一次都是少一个然后多一个,如果少的不是最大值,然后再问新加进来的,看起来很省时间对吧,那么如果少了的是最大值呢?第二个最大值是什么??
那么我们能不能保存上一次的结果呢?当然主要是i的前k-1个数中的最大值了。答案是可以,这就要用到单调队列。
对于单调队列,我们这样子来定义:
- 1、维护区间最值
- 2、去除冗杂状态 如上题,区间中的两个元素a[i],a[j](假设现在再求最大值)
若 j>i且a[j]>=a[i] ,a[j]比a[i]还大而且还在后面(目前a[j]留在队列肯定比a[i]有用,因为你是往后推, 核心思想 !!!)- 3、保持队列单调,最大值是单调递减序列,最小值反之
- 4、最优选择在队首
单调队列实现的大致过程:
1、维护队首(对于上题就是如果队首已经是当前元素的m个之前,则队首就应该被删了,head++)
2、在队尾插入(每插入一个就要从队尾开始往前去除冗杂状态,保持单调性)
简单举例应用
数列为:6 4 10 10 8 6 4 2 12 14
N=10,K=3;
那么我们构造一个长度为3的单调递减队列:
首先,那6和它的位置0放入队列中,我们用(6,0)表示,每一步插入元素时队列中的元素如下
插入6:(6,0);
插入4:(6,0),(4,1);
插入10:(10,2);
插入第二个10,保留后面那个:(10,3);
插入8:(10,3),(8,4);
插入6:(10,3),(8,4),(6,5);
插入4,之前的10已经超出范围所以排掉:(8,4),(6,5),(4,6);
插入2,同理:(6,5),(4,6),(2,7);
插入12:(12,8);
插入14:(14,9);
那么f(i)就是第i步时队列当中的首元素:6,6,10,10,10,10,8,6,12,14
同理,最小值也可以用单调队列来做。
单调队列的时间复杂度是O(N),因为每个数只会进队和出队一次,所以这个算法的效率还是很高的。
注意:建议直接用数组模拟单调队列,因为系统自带容器不方便而且不易调试,同时,每个数只会进去一次,所以,数组绝对不会爆,空间也是S(N),优于堆或线段树等数据结构。
更重要的:单调是一种思想,当我们解决问题的时候发现有许多冗杂无用的状态时,我们可以采用单调思想,用单调队列或类似于单调队列的方法去除冗杂状态,保存我们想要的状态,
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int x,y;
}v[1010000]; //x表示值,y表示位置 可以理解为下标
int a[1010000],n,m,mx[1010000],mn[1010000];
void getmin()
{
int i,head=1,tail=0;// 默认起始位置为1 因为插入是v[++tail]故初始化为0
for(i=1;i<m;i++)
{
while(head<=tail && v[tail].x>=a[i]) tail--;
v[++tail].x=a[i],v[tail].y=i;
// 根据题目 前m-1个先直接进入队列
}
for(;i<=n;i++)
{
while(head<=tail && v[tail].x>=a[i]) tail--;
v[++tail].x=a[i],v[tail].y=i;
while(v[head].y<i-m+1) head++;
mn[i-m+1]=v[head].x;
// 道理同上,当然了 要把已经超出范围的从head开始排出
// 然后每个队首则是目前m个数的最小值
}
}
void getmax() //最大值同最小值的道理,只不过是维护的是递减队列
{
int i,head=1,tail=0;
for(i=1;i<m;i++)
{
while(head<=tail && v[tail].x<=a[i]) tail--;
v[++tail].x=a[i],v[tail].y=i;
}
for(;i<=n;i++)
{
while(head<=tail && v[tail].x<=a[i]) tail--;
v[++tail].x=a[i],v[tail].y=i;
while(v[head].y<i-m+1) head++;
mx[i-m+1]=v[head].x;
}
}
int main()
{
int i,j;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
getmin();
getmax();
for(i=1;i<=n-m+1;i++)
{
if(i==1)printf("%d",mn[i]);
else printf(" %d",mn[i]);
}
printf("\n");
for(i=1;i<=n-m+1;i++)
{
if(i==1)printf("%d",mx[i]);
else printf(" %d",mx[i]);
}
printf("\n");
return 0;
}这就是单调队列,单调栈和单调队列区别不大,都是每次push的时候在栈顶要维护单调性。
关于单调栈的一道题目
问题描述
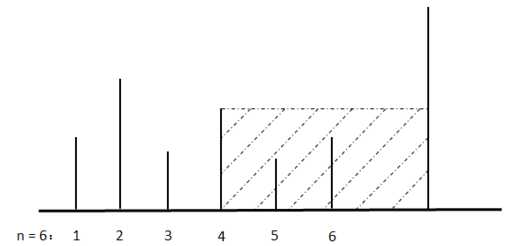
地上从左到右竖立着 n 块木板,从 1 到 n 依次编号,如下图所示。我们知道每块木板的高度,在第 n 块木板右侧竖立着一块高度无限大的木板,现对每块木板依次做如下的操作:对于第 i 块木板,我们从其右侧开始倒水,直到水的高度等于第 i 块木板的高度,倒入的水会淹没 ai 块木板(如果木板左右两侧水的高度大于等于木板高度即视为木板被淹没),求 n 次操作后,所有 ai 的和是多少。如图上所示,在第 4 块木板右侧倒水,可以淹没第 5 块和第 6 块一共 2 块木板,a4 = 2。
解法①
暴力求解,复杂度是O(n2)
例如现在存在5块木板
每块木板从左至右高分别为
10,5,8,12,6
从第一块木板(高度为10)右侧开始倒水,当水到达第四块木板(高度为12)时,可以淹没第一块木板
即第一块木板至第四块木板之间的木板数量,即4-1-1 = 2,a1 = 2;
也就是说:寻找在第 i 个木板右边第一个比它大的木板j,ai 就等于木板 i 和木板 j 之间的木板数
同理得到
a2=0
a3=0
a4=1
a5=0
sum = a1 + a2 +a3 +a4 +a5 = 3
于是,问题就变成了寻找在第 i 个数右边第一个比它大的数。可以暴力求解,从 1 循环到 n,对每块木板再往右循环一遍,这样的时间复杂度是\(O(n2)\) 。
解法②
单调栈来求解的话,复杂度是O(n)
结合单调栈的性质:使用单调栈可以找到元素向左遍历第一个比他小的元素,也可以找到元素向左遍历第一个比他大的元素。
顾名思义,单调栈就是栈内元素单调递增或者单调递减的栈,这一点和单调队列很相似,但是单调栈只能在栈顶操作。
单调栈有以下两个性质:
1、若是单调递增栈,则从栈顶到栈底的元素是严格递增的。若是单调递减栈,则从栈顶到栈底的元素是严格递减的。
2、越靠近栈顶的元素越后进栈。
单调栈与单调队列不同的地方在于栈只能在栈顶操作,因此一般在应用单调栈的地方不限定栈的大小,否则可能会造成元素无法进栈。
元素进栈过程:对于单调递增栈,若当前进栈元素为e,从栈顶开始遍历元素,把小于e或者等于e的元素弹出栈,直接遇到一个大于e的元素或者栈为空为止,然后再把e压入栈中。对于单调递减栈,则每次弹出的是大于e或者等于e的元素。
数据模拟木板倒水单调栈的入栈计算过程
思路:寻找比栈顶高的木板i,找到就出栈,不是就把木板i入栈,给出循环计数样例 10,5,8,12,6
从左往右扫描
栈为空,10入栈 栈:10 此时栈顶是10,也就是说要寻找比10大的木板
5比10小,5入栈 栈:5,10 此时栈顶是5,也就是说要寻找比5大的木板
8比5大,5出栈 栈:10
这个时候,第二个高度为5的木板右边比它高的木板已经找到了,是第三个木板8,所以5出栈,计算a2 = 3-2-1 = 0
8比10小,8入栈 栈:8,10 此时栈顶是8,也就是说要寻找比8大的木板
12比8大,8出栈 栈:10
第三个高度为8的木板右边比它高的木板已经找到了,是第四个木板12,8出栈,计算a3 = 4-3-1 = 0
12比10大,10出栈 栈:空
第一个高度为10的木板右边比它高的木板已经找到了,是第四个木板12,所以10出栈,计算a1 = 4-1-1 = 2
栈为空,12入栈 栈:12 此时栈顶是12,也就是说要寻找比12大的木板
6比12小,6入栈 栈:6,12 此时栈顶是6,也就是说要寻找比6大的木板
扫描完成结束
最后栈的结构是:6,12 栈顶为6
由于最右端竖立着一块高度无限大的木板,即存在第六块木板高度为无穷,所以剩余两块木板的算法如下 a5 = 6-5-1 =0
a4 = 6-4-1 = 1
sum = a1 + a2 +a3 +a4 +a5 = 3
因此本题可以在\(O(n)\)的时间内迎刃而解了。
从左往右将木板节点压栈,遇到比栈顶木板高的木板就将当前栈顶木板出栈并计算淹没的木板数,如此循环直到栈顶木板高度比当前木板高或者栈为空,然后将此木板压栈。木板全都压栈完成后,栈内剩余的木板都是右侧没有比它们更高的木板的,所以一个个出栈并计算ai=n+1-temp_id-1(用最右边无限高的木板减)。
//从左往右解木板倒水
int main() {
int n,ans=0;
cin>>n;
Stack<Node> stack(n);
Node temp;
for(int i=1;i<=n;i++){
cin>>temp.height;
temp.id=i;
//遇到了右侧第一个比栈顶元素大的元素,计算并出栈
while(!stack.empty()&&stack.top().height<=temp.height){
ans=ans+i-stack.top().id-1;
stack.pop();
}
stack.push(temp);
}
//现在栈中的木板右侧没有比它高的木板,用最右侧无限高的木板减
while(!stack.empty()){
ans=ans+n+1-stack.top().id-1;
stack.pop();
}
cout<<ans<<endl;
return 0;
}