斜率优化
如果对于方程形如这样的
我们不能对其进行比较有效果的优化，因为它的转移，涉及到了关于i和关于j的一些数组，这时我们就需要用斜率优化了。
通常我们令k<j<i，且用j来更新F[i]比用j优。则有
并且我们都可以化成如下形式，X[j],Y[j]指只关于j的数，X[k],Y[k]亦之
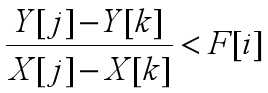
我们可以根据这个式子，来优化DP。这大概就是斜率优化的主要思想
实践出真知，让我们看一下HDU3507吧
很容易可以推出状态转移方程
令k<j<i，那么就可以得到
移项可得
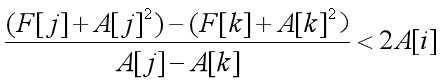
如果我们令Y[i]=F[i]+A[i]²,X[i]=A[i]，那么可以转化成如上形式
优化DP
根据刚才的推算，可以发现，要是满足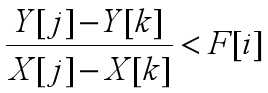这个条件的转移，选j一定比k要优。
我们抽象的把X[i],Y[i]想象成平面上的点，那么这个式子所表示的含义就是两个点所连成的这条线的斜率。
但是这个斜率又是怎么样的呢？
我们令g(i,j)表示i点和j点的斜率（上面式子的左边）。假设g(i,j)<g(j,k)。①如果g(i,j)<F[i]（这个F[i]斜率式子右边的F[i]）那么i一定比j优，则j不必选。②如果g(i,j)>F[i]，那么j比i优，但是k又比j优，还是不选j。
总结出来，如果g(i,j)<g(j,k)，那么j就是废物，可以T掉。
我们发现，这种情况就是
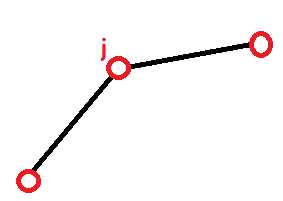
那么最后剩下的图形，就是一个下凸包壳，也就是斜率单调
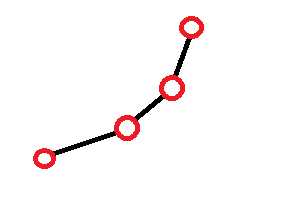
优化实现
我们就例题而言
维护一个单调队列p.get为斜率
表示存的可能为答案的点。因为我们要维护下凸包的性质，必须满足get(p[tail-1],p[tail])>get(p[tail],i)
我们根据斜率式子，队首必须满足get(p[head],p[head+1])<2A[i]
因为斜率越小越优，所以每次选队首。
大致可以有如下代码：
while (head<tail) and (get(p[tail-1],p[tail])>get(p[tail],i)) do dec(tail);
加入新增可供转移的节点
while (head<tail) and (get(p[head],p[head+1])<...) do inc(HeaD)
动态规划转移
