http://www.lydsy.com/JudgeOnline/problem.php?id=3532
如果没有字典序的限制，那么DP拆点最小割即可
加上字典序的限制：
按c从小到大枚举最小割边集中的边，去掉这条边对网络的影响，继续枚举直至获得最小割边集
判断是不是最小割边集中的边：
在残量网络中边的起点和终点不连通
注：最小割边集中的边一定满流，但满流边不一定是最小割边集中的边
如下图所示，流量为1和3的两条边满流，但最小割边集为流量为4的那条边
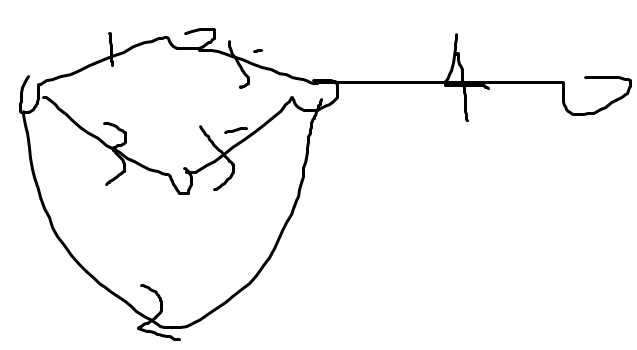
去掉一条边对网络的影响：
边：u-->v
这条边的流量和反向弧的流量置为0
在残量网络上，汇点向v跑一遍最大流，u向源点跑一遍最大流
判断已经得到了最小割中的所有边：
残量网络上，源点和汇点不连通
#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 1410 #define M 520000 const int inf=2e9; int n; int a[N],b[N],c[N]; int f[N]; int tot; int front[N],nxt[M<<1],to[M<<1],val[M<<1],from[M<<1]; int lev[N],num[N]; int path[N]; int cur[N]; int src,decc; int id[N]; bool use[N]; int cnt[N]; int all; int ans[N]; bool vis[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void add(int u,int v,int w) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; from[tot]=u; val[tot]=w; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; from[tot]=v; val[tot]=0; // cout<<u<<‘ ‘<<v<<‘ ‘<<w<<‘\n‘; } bool bfs() { queue<int>q; for(int i=1;i<=all;++i) lev[i]=all; q.push(decc); lev[decc]=0; int now,t; while(!q.empty()) { now=q.front(); q.pop(); for(int i=front[now];i;i=nxt[i]) { t=to[i]; if(lev[t]==all && val[i^1]) { lev[t]=lev[now]+1; q.push(t); } } } return lev[src]!=all; } int augment() { int now=decc,flow=inf; int i; while(now!=src) { i=path[now]; flow=min(flow,val[i]); now=from[i]; } now=decc; while(now!=src) { i=path[now]; val[i]-=flow; val[i^1]+=flow; now=from[i]; } return flow; } void isap() { int flow=0; if(!bfs()) return ; memset(num,0,sizeof(num)); for(int i=1;i<=all;++i) num[lev[i]]++,cur[i]=front[i]; int now=src,t; while(lev[src]<all) { if(now==decc) { flow+=augment(); now=src; } bool advanced=false; for(int i=cur[now];i;i=nxt[i]) { t=to[i]; if(lev[t]==lev[now]-1 && val[i]) { advanced=true; path[t]=i; cur[now]=i; now=t; break; } } if(!advanced) { int mi=all; for(int i=front[now];i;i=nxt[i]) if(val[i]) mi=min(mi,lev[to[i]]); if(!--num[lev[now]]) break; num[lev[now]=mi+1]++; cur[now]=front[now]; if(now!=src) now=from[path[now]]; } } // cout<<flow<<‘\n‘; } void build() { src=1; decc=(n<<1|1)+1; int mx,max_len=0; for(int i=n;i;--i) { mx=0; for(int j=i+1;j<=n;++j) if(a[j]>a[i]) mx=max(mx,f[j]); f[i]=mx+1; max_len=max(max_len,f[i]); } tot=1; memset(front,0,sizeof(front)); for(int i=1;i<=n;++i) { id[i]=tot+1; add(i<<1,i<<1|1,b[i]); } for(int i=1;i<=n;++i) if(f[i]==max_len) add(src,i<<1,inf); for(int i=1;i<=n;++i) if(f[i]==1) add(i<<1|1,decc,inf); for(int i=1;i<=n;++i) for(int j=i+1;j<=n;++j) if(a[j]>a[i] && f[i]==f[j]+1) add(i<<1|1,j<<1,inf); } bool find(int u,int v) { memset(vis,false,sizeof(vis)); queue<int>q; q.push(u); vis[u]=true; int now,t; while(!q.empty()) { now=q.front(); q.pop(); for(int i=front[now];i;i=nxt[i]) { if(!val[i]) continue; t=to[i]; if(!vis[t]) { vis[t]=true; q.push(t); } } } return vis[v]; } void solve() { int sum=0,num=0; int mi; c[0]=inf; memset(use,false,sizeof(use)); while(1) { mi=0; for(int i=1;i<=n;++i) if(!val[id[i]] && !use[i] && c[mi]>c[i]) mi=i; use[mi]=true; if(find(from[id[mi]],to[id[mi]])) continue; ans[++num]=mi; sum+=b[mi]; val[id[mi]]=val[id[mi]+1]=0; src=all; decc=mi<<1|1; isap(); src=mi<<1; decc=1; isap(); src=all; decc=1; if(!bfs()) break; } cout<<sum<<‘ ‘<<num<<‘\n‘; sort(ans+1,ans+num+1); for(int i=1;i<num;++i) cout<<ans[i]<<‘ ‘; cout<<ans[num]<<‘\n‘; } int main() { int T; read(T); while(T--) { read(n); all=(n<<1|1)+1; for(int i=1;i<=n;++i) read(a[i]); for(int i=1;i<=n;++i) read(b[i]); for(int i=1;i<=n;++i) read(c[i]); build(); isap(); solve(); } }
3532: [Sdoi2014]Lis
Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 977 Solved: 362
[Submit][Status][Discuss]
Description
给定序列A，序列中的每一项Ai有删除代价Bi和附加属性Ci。请删除若
干项，使得4的最长上升子序列长度减少至少1，且付出的代价之和最小，并输出方案。
如果有多种方案，请输出将删去项的附加属性排序之后，字典序最小的一种。
Input
输入包含多组数据。
输入的第一行包含整数T，表示数据组数。接下来4*T行描述每组数据。
每组数据的第一行包含一个整数N，表示A的项数，接下来三行，每行N个整数A1．．An，B1．，Bn，C1．．Cn，满足1 < =Ai，Bi，Ci < =10^9，且Ci两两不同。
Output
对每组数据，输出两行。第一行包含两个整数S，M，依次表示删去项的代价和与数量；接下来一行M个整数，表示删去项在4中的的位置，按升序输出。
Sample Input
1
6
3 4 4 2 2 3
2 1 1 1 1 2
6 5 4 3 2 1
6
3 4 4 2 2 3
2 1 1 1 1 2
6 5 4 3 2 1
Sample Output
4 3
2 3 6
解释：删去(A2，43，A6)，(A1，A6)，(A2，43，44，A5)等都是合法的方案，但
{A2，43，A6)对应的C值的字典序最小。
2 3 6
解释：删去(A2，43，A6)，(A1，A6)，(A2，43，44，A5)等都是合法的方案，但
{A2，43，A6)对应的C值的字典序最小。
HINT
1 < =N < =700 T < =5
