http://www.lydsy.com/JudgeOnline/problem.php?id=3144
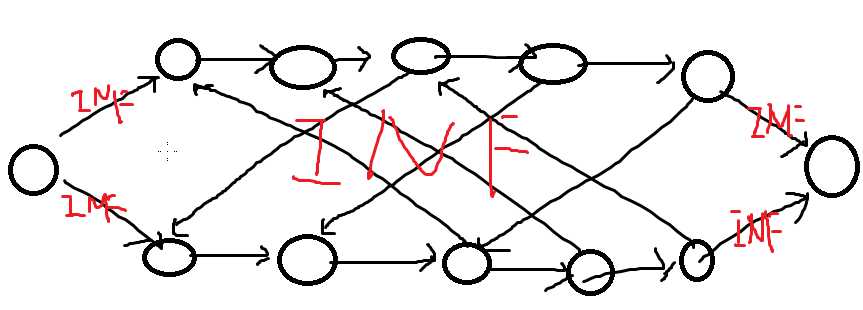
如果D=2 ,两个点,高度为4,建图如下
#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 64005 #define M 323205 const int inf=2e9; int n; int P,Q,R,D; int cost[41][41][41]; int tot=1; int front[N],nxt[M<<1],to[M<<1],val[M<<1],from[M<<1]; int lev[N],num[N]; int path[N]; int cur[N]; int src,decc; int dx[4]={-1,0,1,0}; int dy[4]={0,1,0,-1}; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void add(int u,int v,int w) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; from[tot]=u; val[tot]=w; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; from[tot]=v; val[tot]=0; // cout<<u<<‘ ‘<<v<<‘ ‘<<w<<‘\n‘; } bool bfs() { queue<int>q; for(int i=src;i<=decc;++i) lev[i]=decc; q.push(decc); lev[decc]=0; int now,t; while(!q.empty()) { now=q.front(); q.pop(); for(int i=front[now];i;i=nxt[i]) { t=to[i]; if(lev[t]==decc && val[i^1]) { lev[t]=lev[now]+1; q.push(t); } } } return lev[src]!=decc; } int augment() { int now=decc,flow=inf; int i; while(now!=src) { i=path[now]; flow=min(flow,val[i]); now=from[i]; } now=decc; while(now!=src) { i=path[now]; val[i]-=flow; val[i^1]+=flow; now=from[i]; } return flow; } int isap() { int flow=0; if(!bfs()) return 0; memset(num,0,sizeof(num)); for(int i=src;i<=decc;++i) num[lev[i]]++,cur[i]=front[i]; int now=src,t; while(lev[src]<=decc) { if(now==decc) { flow+=augment(); now=src; } bool advanced=false; for(int i=cur[now];i;i=nxt[i]) { t=to[i]; if(lev[t]==lev[now]-1 && val[i]) { advanced=true; path[t]=i; cur[now]=i; now=t; break; } } if(!advanced) { int mi=decc; for(int i=front[now];i;i=nxt[i]) if(val[i]) mi=min(mi,lev[to[i]]); if(!--num[lev[now]]) break; num[lev[now]=mi+1]++; cur[now]=front[now]; if(now!=src) now=from[path[now]]; } } return flow; } int turn(int i,int j,int k) { return ((i-1)*Q+j-1)*(R+1)+k; } void build() { int nx,ny; for(int i=1;i<=P;++i) for(int j=1;j<=Q;++j) for(int k=1;k<=R;++k) { add(turn(i,j,k),turn(i,j,k+1),cost[i][j][k]); if(k>D) { for(int d=0;d<4;++d) { nx=i+dx[d]; ny=j+dy[d]; if(nx>=1 && nx<=P && ny>=1 && ny<=Q) add(turn(i,j,k),turn(nx,ny,k-D),inf); } } } decc=P*Q*(R+1)+1; for(int i=1;i<=P;++i) for(int j=1;j<=Q;++j) { add(src,turn(i,j,1),inf); add(turn(i,j,R+1),decc,inf); } } int main() { freopen("nutcake.in","r",stdin); freopen("nutcake.out","w",stdout); read(P); read(Q); read(R); read(D); for(int i=1;i<=R;++i) for(int j=1;j<=P;++j) for(int k=1;k<=Q;++k) { read(cost[j][k][i]); // cout<<j<<‘ ‘<<k<<‘ ‘<<i<<‘ ‘<<cost[j][k][i]<<‘\n‘; } build(); cout<<isap(); }
3144: [Hnoi2013]切糕
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 2143 Solved: 1165
[Submit][Status][Discuss]
Description
.jpg)
Input
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1≤x≤P, 1≤y≤Q, 1≤z≤R)。
100%的数据满足P,Q,R≤40,0≤D≤R,且给出的所有的不和谐值不超过1000。
Output
仅包含一个整数,表示在合法基础上最小的总不和谐值。
Sample Input
2 2 2
1
6 1
6 1
2 6
2 6
1
6 1
6 1
2 6
2 6
Sample Output
6
HINT
最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1
