机器学习基石4-在何时才能使用机器学习（4）

            向杜少致敬! 

Lecture 4: Feasibility of Learning

4.1. Learning is Impossible?

 Q1：在训练集 （in-sample） 能找到一个 g ≈ f, 但是你不能保证在应用数据 （out-sample）还有 g ≈ f 。

 Q2：就算在某种约束下，你能保证在应用数据 （out-sample） g ≈ f。 如果我有多个 g ≈ f， 即 g₁ ≈ f、g₂ ≈ f、g₃≈ f、… g_n ≈ f。 如何找到在 out-sample 上性能最好的 g_opt 呢？

4.2. Probalility to the Rescue

    learning 是做不到的！但是我们可以想一下，有没有学习用少量的已知的事实去推测整个样本的情况？ 现在给你一个罐子，你能给出黄绿弹珠所占的比例是多少？ 假设黄绿弹珠的分布较均匀，可以通过抽样的方法获取黄绿弹珠的比例。

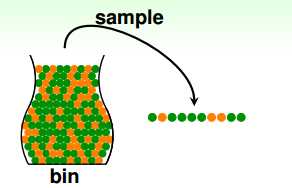
 假设在抽出的样本中 orange marble 的比例是 v， green marble 的比例是 1 -v。 罐子中的 orange marble 的比例是 μ， green marble 的比例是 1-μ。

v 和 μ 基本不相同，那要在什么样的条件下？ v 和 μ 才能足够的接近？在数学中有个 Hoeffding‘s Inequality 能刻画出 v 和 μ 的接近程度。

$$ \mathbb{P} [|\nu -\mu |] \leqslant 2 exp(-2\epsilon^2N)  $$

4.3. Connection to Learning

4.4. Connection to Real Learning