
1、用x1序列的DTFT来表示x2序列的DTFT
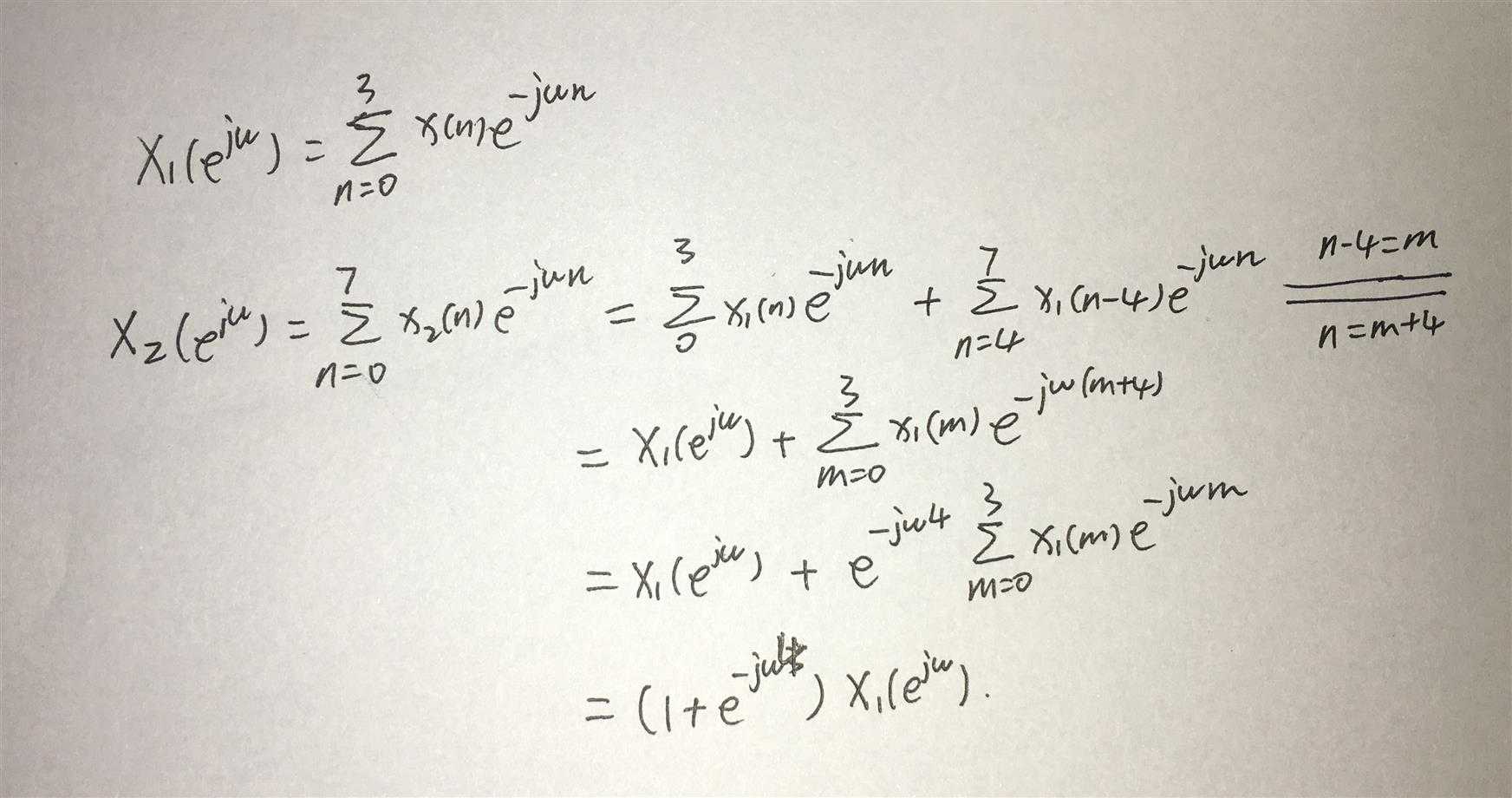
2、代码:
%% ------------------------------------------------------------------------ %% Output Info about this m-file fprintf(‘\n***********************************************************\n‘); fprintf(‘ <DSP using MATLAB> Problem 3.2 \n\n‘); banner(); %% ------------------------------------------------------------------------ % ---------------------------------- % x1(n) % ---------------------------------- n1_start = 0; n1_end = 3; n1 = [n1_start : n1_end]; x1 = [1, 2, 2, 1]; figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 x1(n)‘); set(gcf,‘Color‘,‘white‘); stem(n1, x1); xlabel(‘n‘); ylabel(‘x1‘); title(‘x1(n) sequence‘); grid on; M = 500; k = [-M:M]; % [-pi, pi] %k = [0:M]; % [0, pi] w = (pi/M) * k; [X1] = dtft(x1, n1, w); magX1 = abs(X1); angX1 = angle(X1); realX1 = real(X1); imagX1 = imag(X1); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 DTFT of x1(n)‘);; set(gcf,‘Color‘,‘white‘); subplot(2,1,1); plot(w/pi, magX1); grid on; title(‘Magnitude Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Magnitude‘); subplot(2,1,2); plot(w/pi, angX1); grid on; title(‘Angle Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Radians‘); X1_chk = (1+exp(-j*w*4)) .* X1; magX1_chk = abs(X1_chk); angX1_chk = angle(X1_chk); realX1_chk = real(X1_chk); imagX1_chk = imag(X1_chk); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 X2(w) obtained by formular with X1(w)‘);; set(gcf,‘Color‘,‘white‘); subplot(2,1,1); plot(w/pi, magX1_chk); grid on; title(‘Magnitude Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Magnitude‘); subplot(2,1,2); plot(w/pi, angX1_chk); grid on; title(‘Angle Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Radians‘); % ------------------------------------- % x2(n) % ------------------------------------- [x2, n2] = sigshift(x1, n1, 4); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 x2(n)‘); set(gcf,‘Color‘,‘white‘); stem(n2, x2); xlabel(‘n‘); ylabel(‘x2‘); title(‘x2(n) sequence‘); grid on; M = 500; k = [-M:M]; % [-pi, pi] %k = [0:M]; % [0, pi] w = (pi/M) * k; [X2] = dtft(x2, n2, w); magX2 = abs(X2); angX2 = angle(X2); realX2 = real(X2); imagX2 = imag(X2); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 DTFT of x2(n)‘);; set(gcf,‘Color‘,‘white‘); subplot(2,1,1); plot(w/pi, magX2); grid on; title(‘Magnitude Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Magnitude‘); subplot(2,1,2); plot(w/pi, angX2); grid on; title(‘Angle Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Radians‘); % ------------------------------------- % x3(n) % ------------------------------------- [x3, n3] = sigadd(x1, n1, x2, n2); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 x3(n)‘); set(gcf,‘Color‘,‘white‘); stem(n3, x3); xlabel(‘n‘); ylabel(‘x3‘); title(‘x3(n) sequence‘); grid on; M = 500; k = [-M:M]; % [-pi, pi] %k = [0:M]; % [0, pi] w = (pi/M) * k; [X3] = dtft(x3, n3, w); magX3 = abs(X3); angX3 = angle(X3); realX3 = real(X3); imagX3 = imag(X3); figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 3.2 DTFT of x3(n)‘);; set(gcf,‘Color‘,‘white‘); subplot(2,1,1); plot(w/pi, magX3); grid on; title(‘Magnitude Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Magnitude‘); subplot(2,1,2); plot(w/pi, angX3); grid on; title(‘Angle Part‘); xlabel(‘frequency in \pi units‘); ylabel(‘Radians‘);
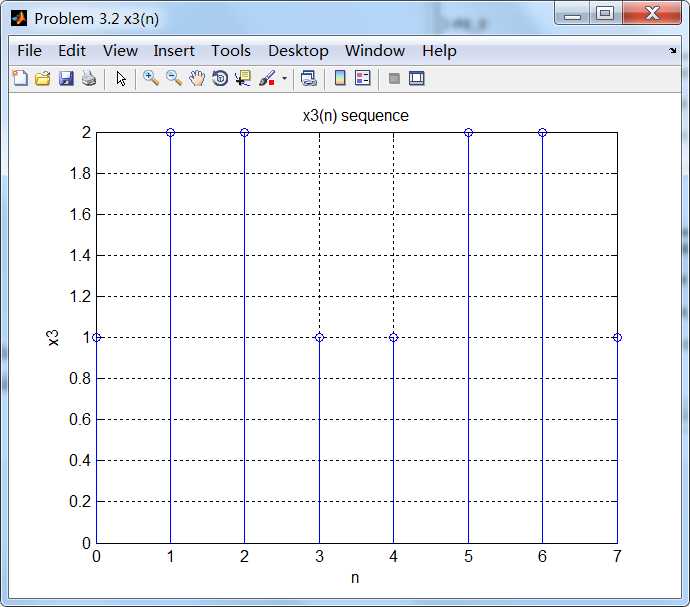
运行结果:
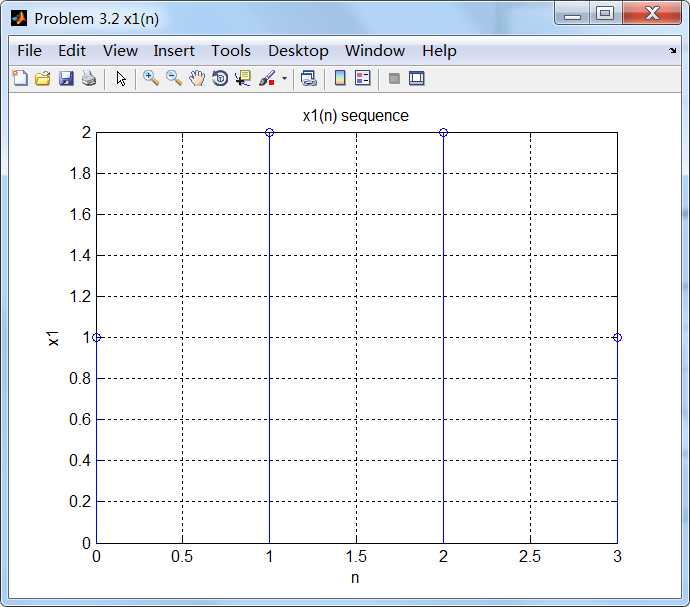
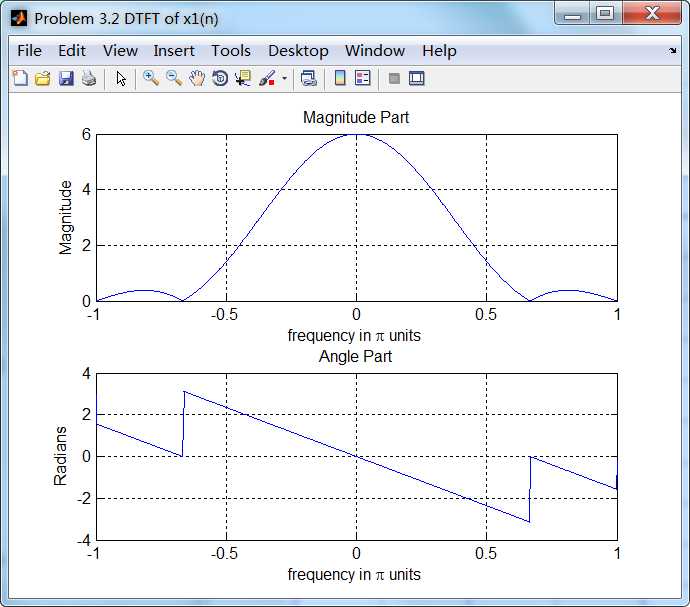
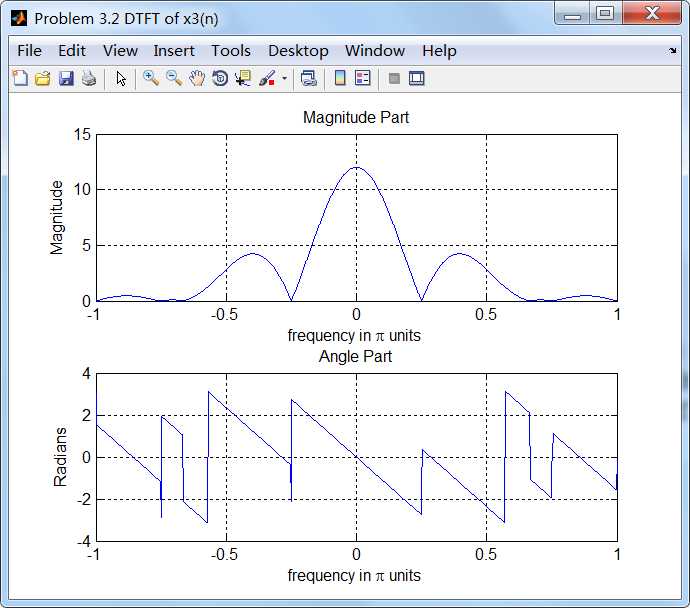
通过第1小题得到的公式计算x2序列的谱,如下:
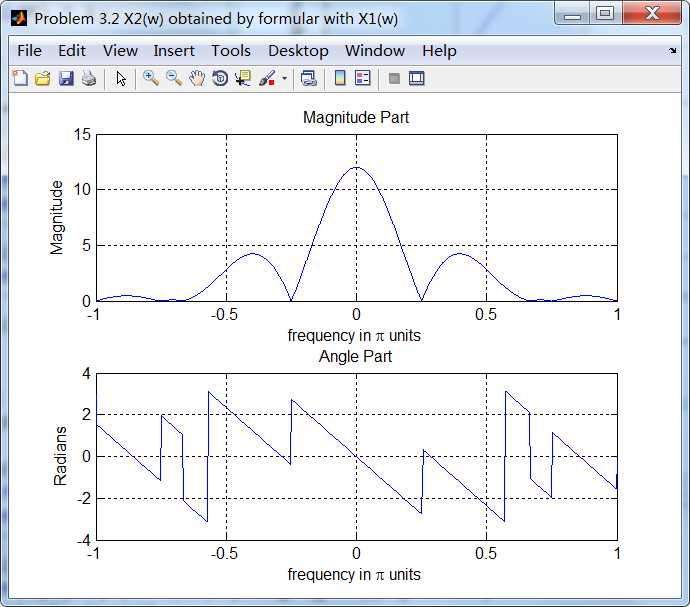
可看出,第1小题公式计算的结果,和直接将序列通过DTFT定义得到结果是相同的。
