码迷，mamicode.com
首页 > 其他好文 > 详细

# 2017-2018-1 20155337《信息安全系统设计基础》第十三周学习总结

时间：2017-12-17 18:07:18      阅读：216      评论：0      收藏：0      [点我收藏+]

标签：temporary   read   block   版本   cache   int   oid   ons   body   

2017-2018-1 20155337《信息安全系统设计基础》第十三周学习总结

我认为本书重要的一章也是我学的比较不错的一章就是第六章
--存储器层次结构。

存储技术

  • 1、 基本的存储技术包括随机存储器（RAM）、非易失性存储器（ROM）和磁盘。RAM分静态RAM（SRAM）和动态RAM（DRAM）。SRAM快些，也贵些，主要用做CPU芯片上的高速缓存，也可以用作芯片下的高速缓存。DRAM慢些，便宜些，主要用作驻村和图形帧缓冲区。ROM也叫做只读存储器，即使在断电的情况下，也能保持他们的信息，它们用来存储固件。
  • 2、传统的DRAM芯片单元被分成d个超单元，每个超单元由w个DRAM单元组成。一个dxW的DRAM总共存储了dw位信息。一个16x8的DRAM芯片组织如下图所示：
    技术分享图片
  • 3、电路设计者将DRAM组织成二维阵列而不是线性数组的一个原因是降低芯片上地址引脚的数量。（因为每个引脚一次只能传送一位）读一个DRAM超单元内容的方式如下图所示：
    技术分享图片
    DRAM芯片包装在存储器模块中，示例模块用8个64Mbit的8Mx8的DRAM芯片，总共存储64MB（兆字节），如下图所示：
    技术分享图片
  • 4、增强的DRAM：FPM DRAM , EDO DRAM , SDRAM , DDR DRAM , RDRAM , VRAM。

  • 5、访问主存，数据流通过总线在CPU和DRAM主存之间来来回回。
    movl A, %eax指令会发生如下流程：
    技术分享图片
    技术分享图片
    技术分享图片
    movl %eax, A指令会发生如下流程：
    技术分享图片
    技术分享图片
    技术分享图片
    6、磁盘存储（基本都没看）
    固态硬盘是一种基于闪存的存储技术。

    局部性

  • 1、局部性通常分两种不同的形式，时间局部性和空间局部性。有良好局部性的程序比局部性差的程序运行的更快。在一个有良好时间局部性的程序中，被引用过一次的存储器位置很可能在不远的将来被多次引用；具有良好控件局部性的程序中，如果一个存储器被引用一次，那么程序可能在不久的将来引用附近的一个存储器位置。

  • 2、对程序数据引用的局部性

a）一维数组示例如下：
技术分享图片
对于sum来说，有很好的时间局部性，因为sum是标量，对于sum来说，没有空间局部性；对于变量v，有很好的控件局部性，但是因为每个向量元素只被访问一次，因此时间局部性很差。因此，总体来说，sumvec函数有很好的局部性。

b）二维数组示例如下：
该段代码有很好的局部性：
技术分享图片
该段代码局部性不好：
技术分享图片

  • 3、取指令局部性
    因为程序指令是存放在存储器中的，CPU必须取出这些指令，所以我们也能评价一个程序关于取指令的局部性。例如，上述一维数组示例中，for循环中的指令是按照连续的存储器顺序执行的，因此循环有良好的空间局部性。因为循环体会被执行多次，所以也有很好的时间局部性。
  • 4、局部性小结
    一些量化评价一个程序中局部性的简单原则：
    重复引用同一个变量从的程序有良好的时间局部性；
    对于步长为k的引用模式的程序，步长越小，空间局部性越好。具有步长为1的引用模式的程序有很好的空间局部性；
    对于取指令来说，循环有很好的时间和空间局部性。循环体越小，循环迭代次数越多，局部性越好。

三、存储器层次结构

存储器层次结构的中心思想是，对于每个k，位于k层的更快更小的存储设备作为位于k+1层的更大更慢的存储设备的缓存。数据总是以块大小作为传送单元在第k层和k+1层之间来回拷贝的。存储器层次结构示例如下图所示：
技术分享图片
几个基本术语：缓存命中，缓存不命中（冷不命中，冲突不命中，容量不命中）

四、高速缓存存储器

  • 1、通用的高速缓存存储器结构
    技术分享图片技术分享图片
    （m=t+s+b）
  • 2、直接映射高速缓存
    每组只有一行的高速缓存叫直接映射高速缓存。高速缓存确定一个请求是否命中，然后抽取出被请求的字的过程，分为三步：
  • 1）组选择
  • -2）行匹配
  • -3）字抽取

a）组选择
技术分享图片
b）直接映射高速缓存行匹配
当且仅当设置了有效位，而且告诉缓存行中的标记与w的地址中标记相匹配时，这一行中包含w的一个拷贝。（有效位+标记）

c）直接映射高速缓存中的子选择块偏移位提供了所需要的字的第一个字节的偏移。
技术分享图片

  • 3、综合示例
    假设我们有一个直接映射高速缓存，描述如下：（S，E，B，m）=（4,1,2,4），即4个组，每个组1行，每个块2个字节，地址是4位。这里假设每个字都是单字节，每次都读1个字。由上得知，
    技术分享图片
    技术分享图片
    射高速缓存的4位地址空间
    示例过程如下：初始时，高速缓存是空的：
    技术分享图片
    a）读地址0的字。因为组0的有效位是0，缓存不命中，所以高速缓存从存储器取出块0，，并存储在组0中。然后高速缓存返回取出的高速缓存行的m[0]。
    技术分享图片
    b）读地址1的字。高速缓存命中。

c）度地址13的字。
技术分享图片
d）读地址8的字。（组0的行确实有效，但标记不匹配）
技术分享图片
e）读地址0的字。又发生缓存不命中，因为前面引用地址8时，刚好替换了块8。
技术分享图片

  • 6、直接映射高速缓存中的冲突不命中
    以下代码容易产生抖动问题：
    技术分享图片
    简单来说，即使程序有良好的空间局部性，而且我们的高速缓存中也有足够的空间来存放x[i]和y[i]的块，每次引用还是会引起冲突不命中，这是因为这些块被映射到了同一个高速缓存组。参考如下表：
    技术分享图片
    采用如下方法，可以消除抖动，把x定义为float x[12]，在x结尾加了填充，x[i]和y[i]现在就映射到了不同的组：
    技术分享图片
    7、组相连高速缓存：每个组都保存有多于一个的高速缓存行。
    8、全相联高速缓存：只有一个组，这个组包含所有的高速缓存行。

家庭作业

  • 6.22
    技术分享图片

假设磁道沿半径均匀分布，即总磁道数和(1-x)r成正比，设磁道数为(1-x)rk；

由题单个磁道的位数和周长成正比，即和半径xr成正比，设单个磁道的位数为xrz；

其中r、k、z均为常数。

所以C = (1-x)rk * xrz = (-x^2 + x) * r^2 * kz，即需要-x^2 + x最大，得到x = 0.5。

  • 6.23
    技术分享图片

seek time : 4 ms

average rotational latency : 0.5 * 60 / 15000 * 1000 = 2 ms

transfer time : 60 / 15000 / 800 * 1000= 0.005 ms

4 + 2 + 0.005 = 6.005 ms

  • 6.24
    技术分享图片

技术分享图片

A.

2MB = 512 bytes * 4096，即需要读取4096个扇区。

定位时间为：4 + 0.560/150001000 = 6 ms

最理想的情况下，这4096个扇区都在一个柱面上（一个磁道读完后继续读下一个，磁头不用移动），也就是4096/1000 = 5个磁道。

即transfer time = 4096 / 1000 * 60 / 15000 * 1000 = 16.384 ms

所以理想时间为：6 + 16.384 = 22.384 ms

B.

2MB = 512 bytes * 4096，即需要读取4096个扇区。

定位时间为：4 + 0.560/150001000 = 6 ms

在完全随机的情况下，这4096个扇区分布在不同的磁道上，每一个扇区读完以后磁头都要再次去定位。

所以总的时间为：6 * 4096 + transfer time = 24592.384 ms （这里书上有一个类似的题目，但是没有加上transfer time ，我觉得还是要加上）

  • 6.25
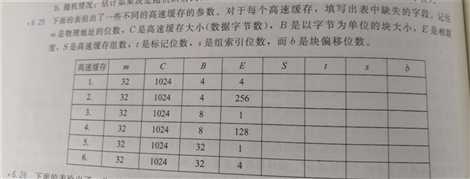
    技术分享图片
 ·  S      t    s     b
1. 64    24    6    2
2. 1     30    0    2
3. 128   22    7    3
4. 1     29    0    3
5. 32    22    5    5
6. 8     24    3    5
  • 6.26
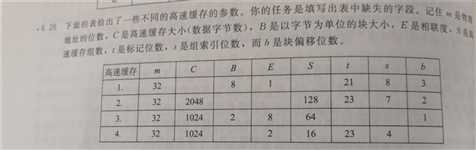
    技术分享图片
·   m    C    B    E    S    t    s    b
1.      2048           256
2.            4    4
3.                           25   6
4.            32                       5
  • 6.27
    技术分享图片

A.

0x08A4 0x08A5 0x08A6 0x08A7

0x0704 0x0705 0x0706 0x0707

B.

0x1238 0x1239 0x123A 0x123B

  • 6.28
    技术分享图片

A.

None

B.

0x18F0 0x18F1 0x18F2 0x18F3

0x00B0 0x00B1 0x00B2 0x00B3

C.

0x0E34 0x0E35 0x0E36 0x0E37

D.

0x1BDC 0x1BDD 0x1BDE 0x1BDF

  • 6.29
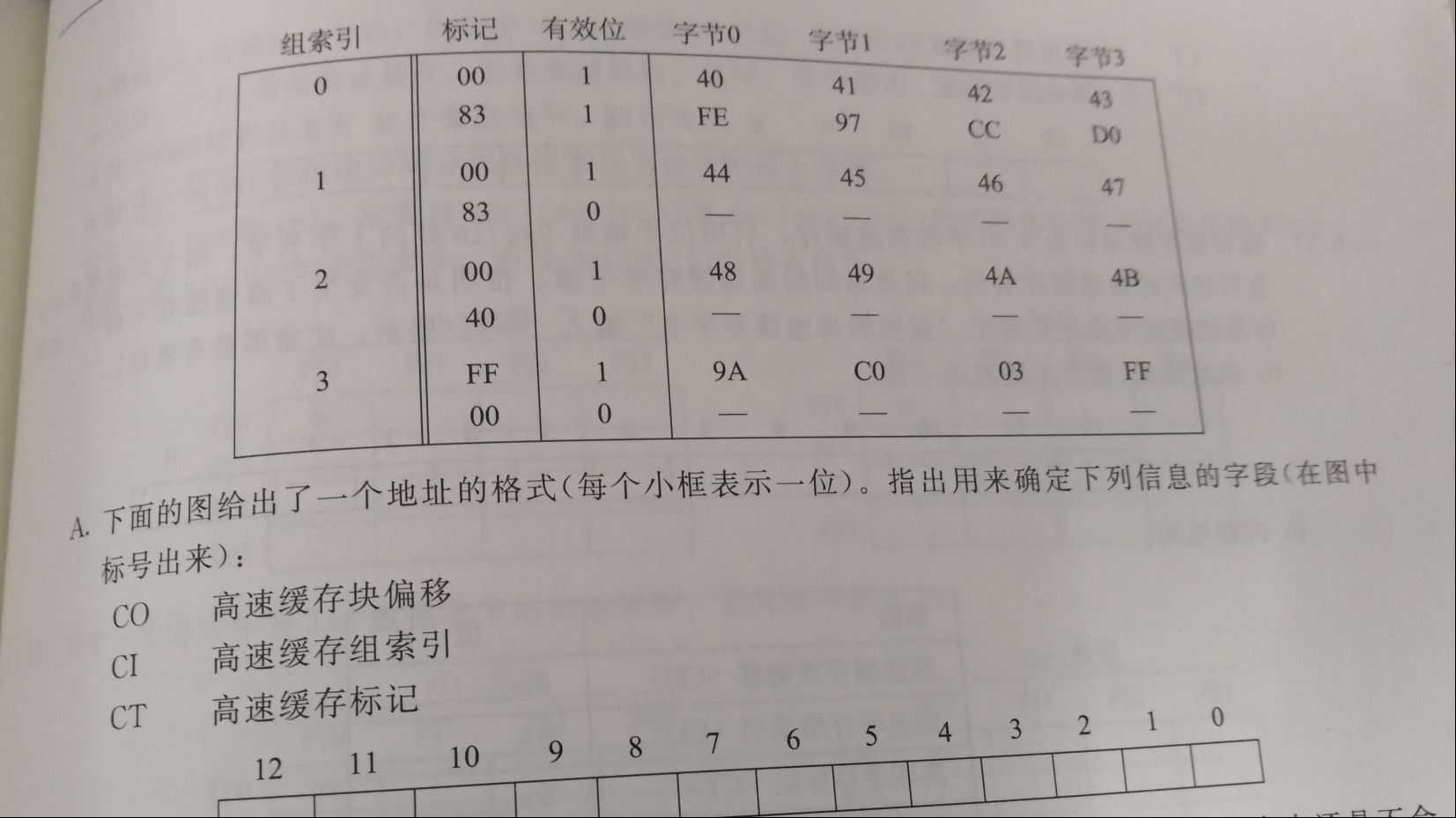
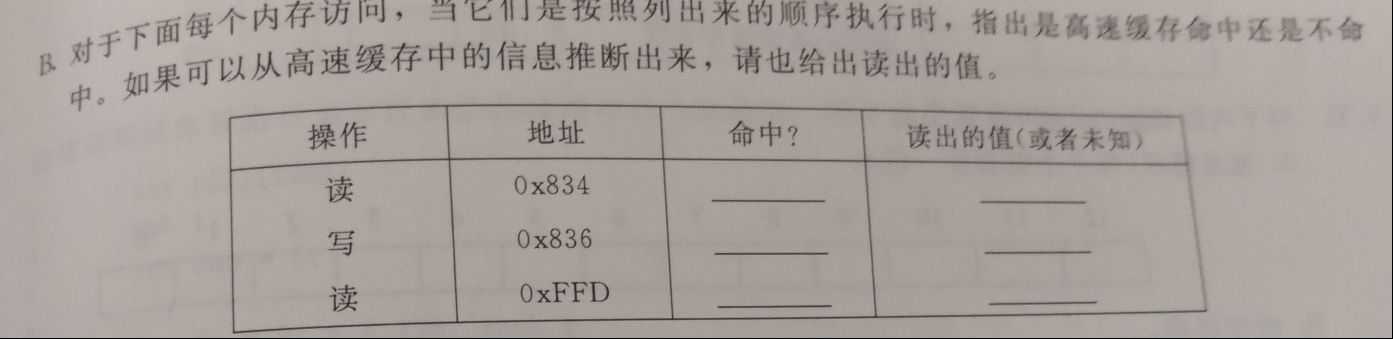
    技术分享图片

技术分享图片

技术分享图片

A.

CTCTCTCTCTCTCTCT, CICI, COCO

B.

Hit?    Read value(or unknown)
N           -
Y           unknown
Y           0xC0
  • 6.30
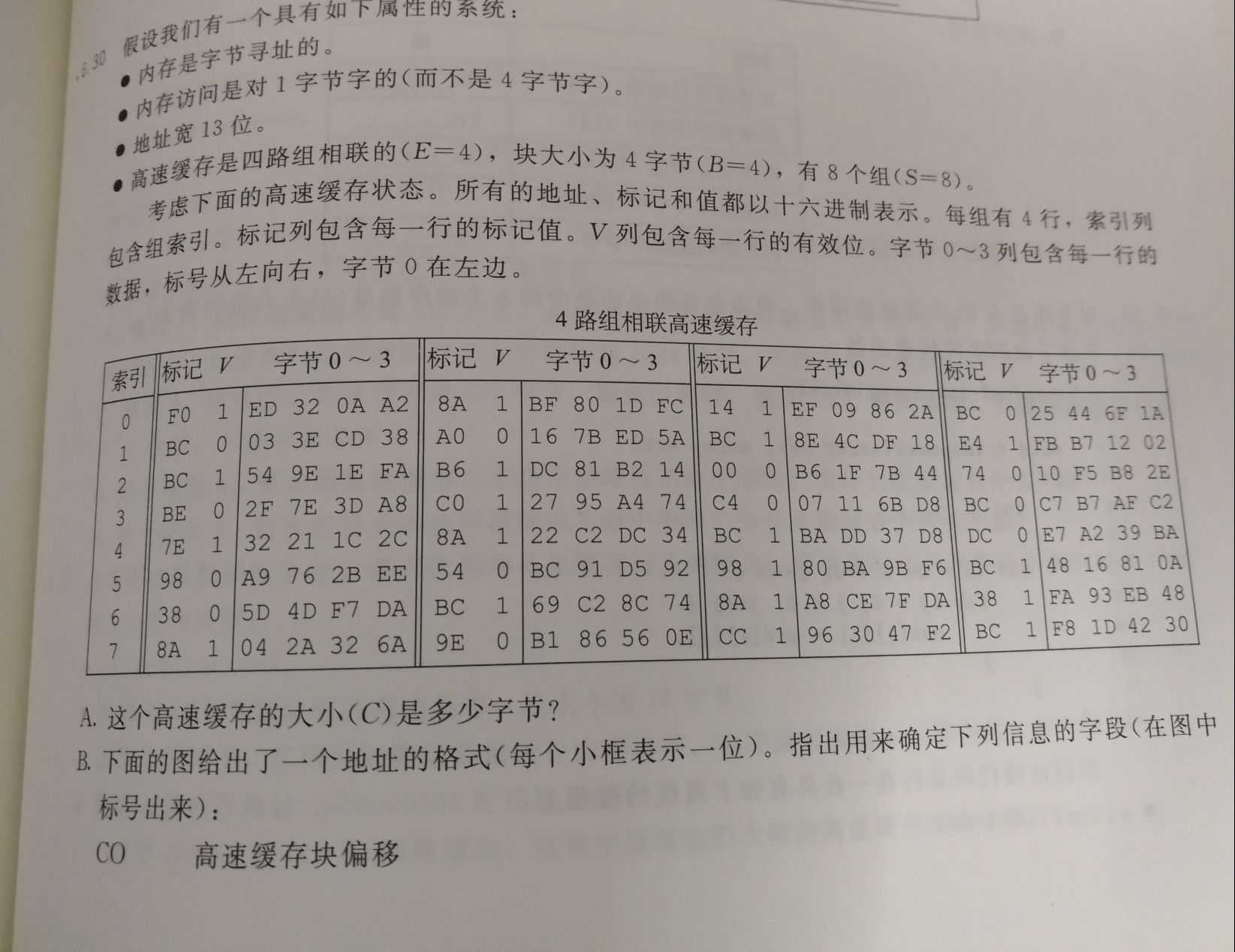
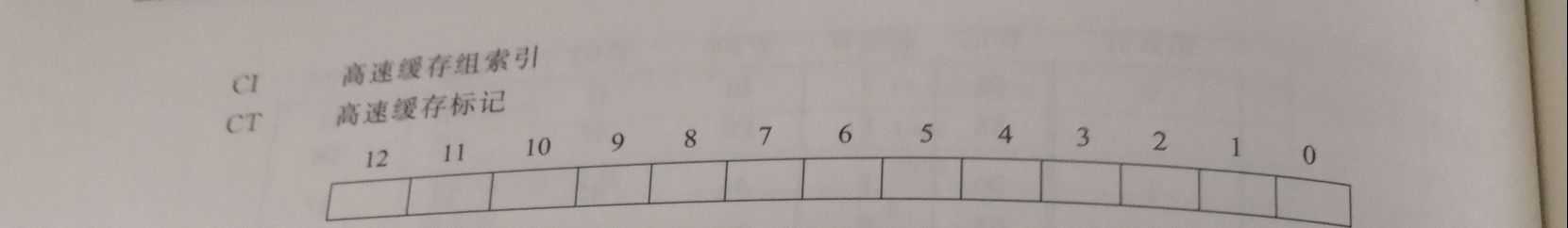
    技术分享图片
    技术分享图片

A.

C = S * E * B = 128 Bytes

B.

CTCTCTCTCTCTCTCT, CICICI, COCO

  • 6.31
    技术分享图片

A.

00111000, 110, 10

B.

CO 0x2

CI 0x6

CT 0x38

Cache hit? Y

Cache byte returned 0xEB

  • 6.32
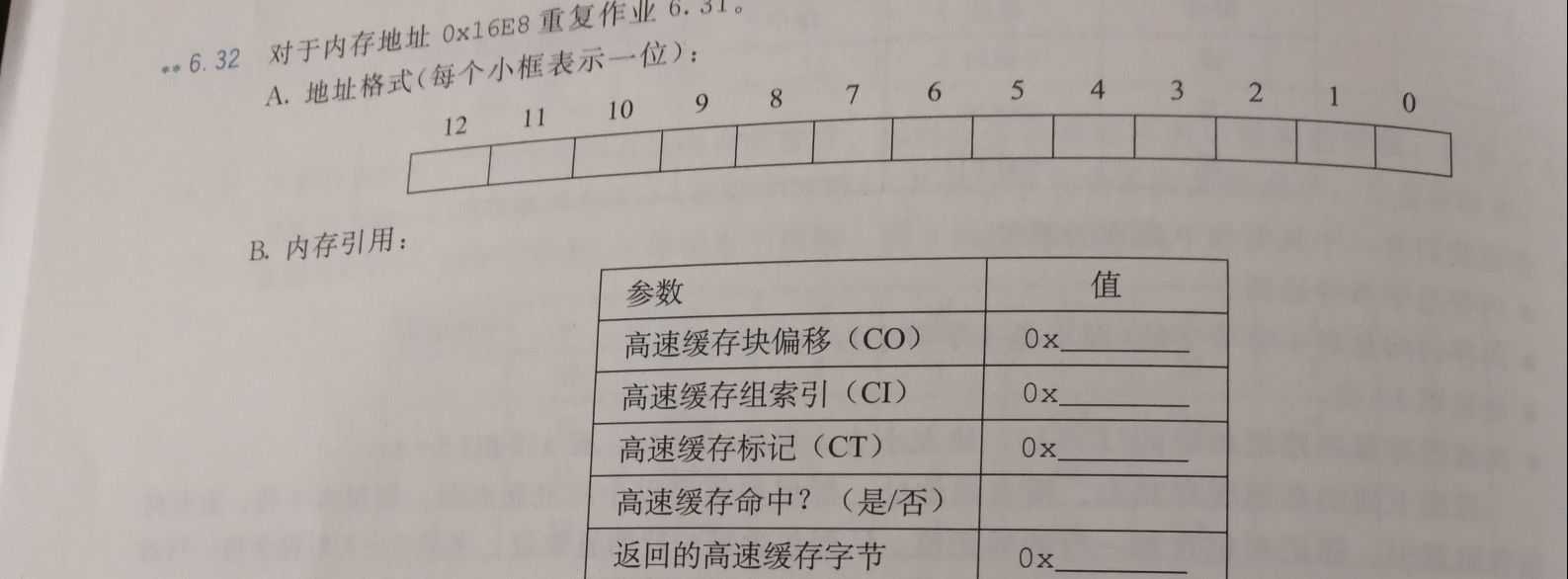
    技术分享图片

A.

10110111, 010, 00

B.

CO 0x0

CI 0x2

CT 0xB7

Cache hit? N

Cache byte returned -

  • 6.33
    技术分享图片

0x1788 0x1789 0x178A 0x178B

0x16C8 0x16C9 0x16CA 0x16CB

  • 6.34
    技术分享图片
    技术分享图片

cache共有两个block，分别位于两个set中，设他们为b1和b2。每个block可以放下4个int类型的变量，也就是数组中的一行。在这一题中，源数组和目的数组是相邻排列的。所以内存和cache的映射情况是这样的：

b1 : src[0][] src[2][] dst[0][] dst[2][]

b2 : src[1][] src[3][] dst[1][] dst[3][]

    dst array                                   src array
       Col.0  Col.1  Col.2  Col.3                 Col.0  Col.1  Col.2  Col.3
Row0     m      m       h     m                    m       m      m      m
Row1     m      h       m     h                    m       m      m      m
Row2     m      m       h     m                    m       m      m      m
Row3     m      h       m     h                    m       m      m      m
  • 6.35
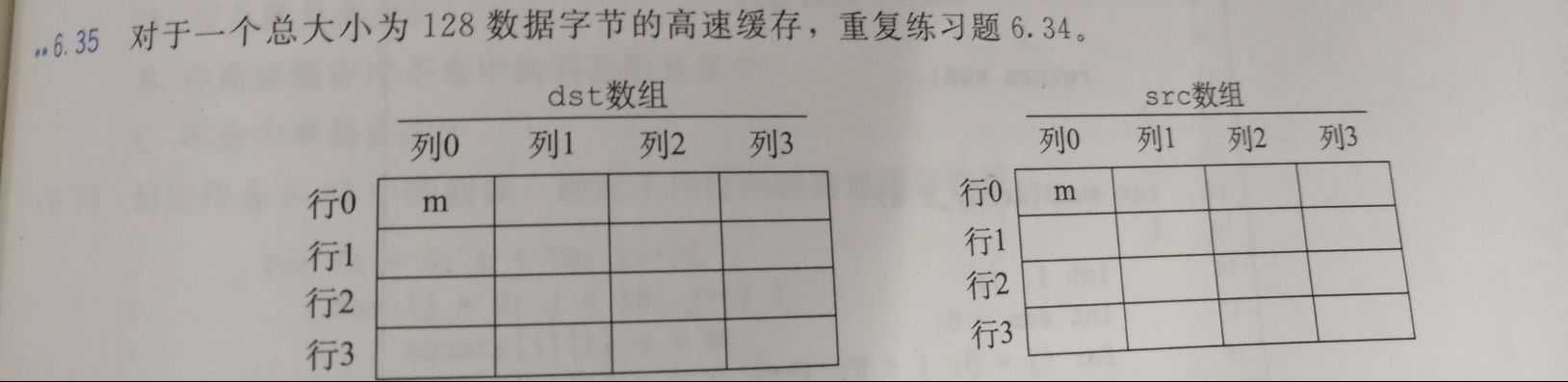
    技术分享图片

cache共有八个block，分别位于八个set中，设他们为b1、b2、b3、b4、b5、b6、b7、b8。每个block可以放下4个int类型的变量，也就是数组中的一行。在这一题中，源数组和目的数组是相邻排列的。所以内存和cache的映射情况是这样的：（这时不会有冲突）

b1 : src[0][]

b2 : src[1][]

b3 : src[2][]

b4 : src[3][]

b5 : dst[0][]

b6 : dst[1][]

b7 : dst[2][]

b8 : dst[3][]

  dst array                                   src array
       Col.0  Col.1  Col.2  Col.3                 Col.0  Col.1  Col.2  Col.3
Row0     m      h      h      h                     m      h      h      h
Row1     m      h      h      h                     m      h      h      h
Row2     m      h      h      h                     m      h      h      h
Row3     m      h      h      h                     m      h      h      h
  • 6.36
    技术分享图片

A.

cache共有32个block，分别位于32个set中，每个block可以放下4个int类型的变量，所以所有的block可以放下x数组中的一行。由映射关系，x[0][i]和x[1][i]对应的set是一样的。所以每一次的运算都会发生miss的情况，所以miss rate = 100%。

B.

cache共有64个block，分别位于64个set中，每个block可以放下4个int类型的变量，所以所有的block可以放下x数组中的两行，即全部放入。每四次读取中的第一次会发生miss，所以miss rate = 25%。

C.

cache共有32个block，分别位于16个set中，每个block可以放下4个int类型的变量，每个set可以放下8个int类型的变量，所有的block可以放下x数组中的一行。由映射关系，x[0][i]和x[1][i]对应的set是一样的，x[y][i]和x[y][i+64]对应的set也是一样的。

对于x[0][0] * x[1][0] ~ x[0][63] * x[1][63] ，每四次运算会有第一次miss。

对于x[0][64] * x[1][64] ~ x[0][127] * x[1][127] ，每四次运算会有第一次miss（擦去前面warm up的cache）。

综上，miss rate = 25%。

D.

不会，因为此时block大小是限制因素（每四次读取第一次miss）。

E.

会，更大的block会降低miss rate，因为miss只发生在第一次读入block的时候，所以更大的block会使得miss占总读取的比例降低。

  • 6.37
    技术分享图片

技术分享图片

cache共有256个block，分别位于256个set中，每个block可以放下4个int类型的变量，所有的block可以放下1024个int类型的变量。

当N = 64：

映射关系：a[0][0] ~ a[15][63]、a[16][0] ~ a[31][63]、a[32][0] ~ a[47][63]、a[48][0] ~ a[63][63] 互相重叠。

sumA按照行来读取，所以每四次读取第一次都会miss，即miss rate = 25%。

sumB按照列来读取，所以每一次读取都会发生miss（读取后的block又会被覆盖），即miss rate = 100%。

sumC按照列来读取，但是每次读取后都会按照行再读取一次，所以每四次读取会有两次miss，即miss rate = 50%。

当N = 60

映射关系：a[0][0] ~ a[17][3]、a[17][4] ~ a[34][7]、a[34][8] ~ a[51][11]、a[51][12] ~ a[59][59]互相重叠，其中最后的a[51][12] ~ a[59][59]没有到达cache的尾部。

sumA按照行来读取，所以每四次读取第一次都会miss，即miss rate = 25%。

sumB按照列来读取，这里的情况有些复杂，我写了一个程序来分析：

#include <stdio.h>

#define SIZEOFCACHE 256
#define SIZEOFBLOCK 4
#define N 60


int main()
{
    int cache[SIZEOFCACHE];
    for (int k = 0; k < SIZEOFCACHE; ++k)
    {
        cache[k] = -1;
    }

    int read = 0;
    int miss = 0;
    for (int j = 0; j < N; ++j)
    {
        for (int i = 0; i < N; ++i)
        {
            //read a[i][j]
            ++read;
            int position = i * N + j;
            int need_start = position/SIZEOFBLOCK;
            if (cache[need_start%SIZEOFCACHE] != need_start)
            {
                ++miss;
                cache[need_start%SIZEOFCACHE] = need_start;
            }
        }
    }

    printf("%g\n", miss/(double)read);

    return 0;
}

输出结果为25%。

C.

将上面程序的循环部分更改为：

for (int j = 0; j < N; j+=2)
    {
        for (int i = 0; i < N; i+=2)
        {
            //read a[i][j] a[i+1][j] a[i][j+1] a[i+1][j+1]
            ++read;
            int position = i * N + j;
            int need_start = position/SIZEOFBLOCK;
            if (cache[need_start%SIZEOFCACHE] != need_start)
            {
                ++miss;
                cache[need_start%SIZEOFCACHE] = need_start;
            }

            ++read;
            position = (i+1) * N + j;
            need_start = position/SIZEOFBLOCK;
            if (cache[need_start%SIZEOFCACHE] != need_start)
            {
                ++miss;
                cache[need_start%SIZEOFCACHE] = need_start;
            }

            ++read;
            position = i * N + j + 1;
            need_start = position/SIZEOFBLOCK;
            if (cache[need_start%SIZEOFCACHE] != need_start)
            {
                ++miss;
                cache[need_start%SIZEOFCACHE] = need_start;
            }

            ++read;
            position = (i+1) * N + j + 1;
            need_start = position/SIZEOFBLOCK;
            if (cache[need_start%SIZEOFCACHE] != need_start)
            {
                ++miss;
                cache[need_start%SIZEOFCACHE] = need_start;
            }
        }
    }

输出结果为25%。

  • 6.38
    技术分享图片
    技术分享图片

这个cache有64个block，每个block可以放4个int类型的变量，也就是一个point_color的结构体，即cache总共可以放置64个结构体。

映射关系为：square[0][0] ~ square[3][15]、square[4][0] ~ square[7][15]、square[8][0] ~ square[11][15]、square[12][0] ~ square[15][15] 互相重叠。

A.

16 * 16 * 4 = 1024

B.

这个程序是按照行来写的，所以每四次写入只有第一次miss，即miss的次数为1024 / 4 = 256

C.

25%

  • 6.39
    技术分享图片

这个cache有64个block，每个block可以放4个int类型的变量，也就是一个point_color的结构体，即cache总共可以放置64个结构体。

映射关系为：square[0][0] ~ square[3][15]、square[4][0] ~ square[7][15]、square[8][0] ~ square[11][15]、square[12][0] ~ square[15][15] 互相重叠。

A.

16 * 16 * 4 = 1024

B.

这个程序是按照列来写的，每四次写入只有第一次miss（每次都完整利用了一个block，没有读入block的浪费，此时miss rate只取决于block的大小），即miss的次数为1024 / 4 = 256

C.

25%

  • 6.40
    技术分享图片

这个cache有64个block，每个block可以放4个int类型的变量，也就是一个point_color的结构体，即cache总共可以放置64个结构体。

映射关系为：square[0][0] ~ square[3][15]、square[4][0] ~ square[7][15]、square[8][0] ~ square[11][15]、square[12][0] ~ square[15][15] 互相重叠。

A.

16 * 16 + 3 * 16 * 16 = 1024

B.

对于第一个循环，每一次写入都会发生miss的情况，最后cache中保存的是square[12][0] ~ square[15][15]，而第二个循环又从头开始写入，所以每三次写入的第一次都会发生miss。总的miss次数就是16 * 16 * 2 = 512。

C.

50%

  • 6.41
    技术分享图片

技术分享图片

这个cache有16K个block，每个block可以放4个char类型的变量，也就是一个pixel的结构体，即cache总共可以放置16K个结构体。buffer里面一共有480 * 640 = 300K个结构体，所以映射时会有18个完全重叠的，最后一次重叠3/4.

这个程序按照列来写，每四次写入只有第一次miss（每次都完整利用了一个block，没有读入block的浪费，此时miss rate只取决于block的大小），所以miss rate = 25%。

  • 6.42
    技术分享图片

这个cache有16K个block，每个block可以放4个char类型的变量，也就是一个pixel的结构体，即cache总共可以放置16K个结构体。buffer里面一共有480 * 640 = 300K个结构体，所以映射时会有18个完全重叠的，最后一次重叠3/4.

这个程序实际上就是按照行来写的指针版本，每四次写入只有第一次miss，miss rate = 25%。

  • 6.43
    技术分享图片

这个cache有16K个block，每个block可以放4个char类型的变量，也就是一个pixel的结构体，即cache总共可以放置16K个结构体。buffer里面一共有480 * 640 = 300K个结构体，所以映射时会有18个完全重叠的，最后一次重叠3/4.

这个程序实际上还是按照行来写的指针版本，但是只写了buffer数组的1/4。每四次写入只有第一次miss，miss rate = 25%。

  • 6.44
    技术分享图片

为了辨识缓存的大小，选取中间的列（例如S8）来判断——避免CPU的prefetching带来干扰。可以看出，在32K和512K以及8M的地方有明显的落差，所以判断L1:32k、L2:512k、L3:8M。
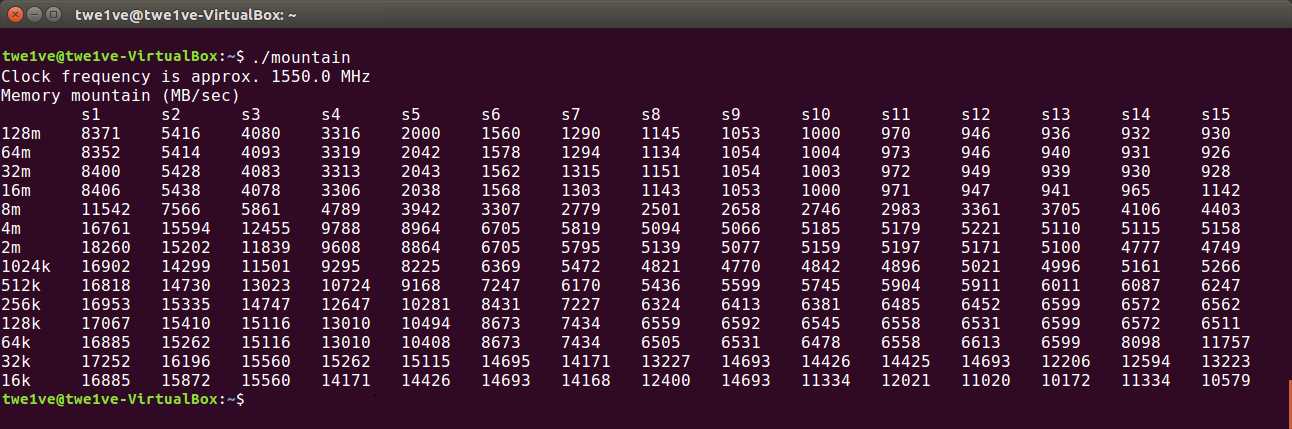
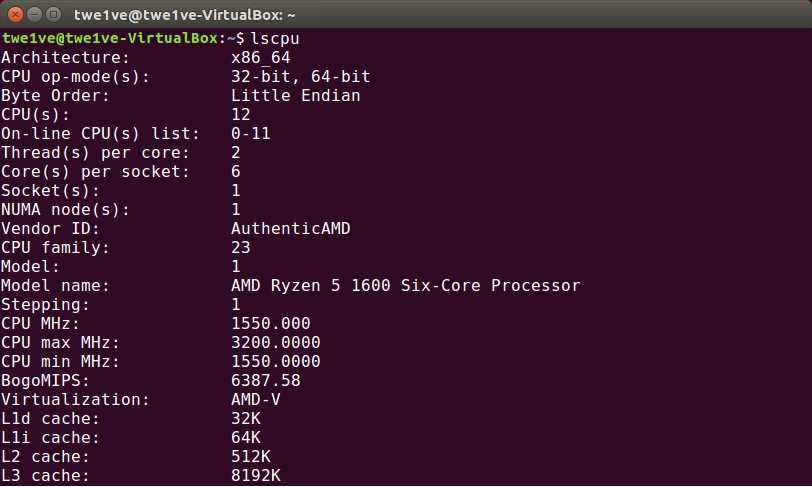
技术分享图片

用lscpu验证分析正确：
技术分享图片

  • 6.45
    技术分享图片

这个题要求我们利用第5章和第6章中学到的优化知识。对于第5章，就是减少循环的数据依赖，从而利用流水线并行执行；对于第6章，则是从两个方面（temporary、spatial）利用数据的“本地性”。

void transpose(int *dst, int *src, int dim)
{
    int i, j;
    for (i = 0; i < dim; ++i)
    {
        for (j = 0; j < dim; ++j)
        {
            dst[j*dim + i] = src[i*dim +j] /* ! */
        }
    }
}

以上的关键语句中的乘法和加法已经实现了循环之间独立，src也是按照行读入的，但是dst却是按照列读入的，这样没有充分利用每一次读入的block。于是我们想到可不可以每一次读入dst[j*dim + i]所在的block之后继续写入例如dst[j*dim + i + 1] dst[j*dim + i + 2]这样的变量，但是这样有需要src的部分变为src[(i+1)*dim +j]等等，所以我们现在不仅要“横向”扩展dst，还要“纵向”扩展src，其实这是一种叫做blocking的技术，即每次读入一块数据，对此块数据完全利用后抛弃，然后读取下一个块。可以参考csapp网上给的注解：MEM:BLOCKING — Using blocking to increase temporal locality

设我们的数据块的宽度是B，由于我们要对两个数组进行读写操作，所以2B^2 < C（其中C是cache的容量），在此限制下B尽可能取大。

#define B chunkdatas_length_of_side
void faster_transpose(int *dst, int *src, int dim)
{
    long limit = dim * dim;
    for (int i = 0; i < dim; i += B)
    {
        for (int j = 0; j < dim; j += B)
        {
            /* Using blocking to improve temporal locality */

            for (int k = i; k < i+B; ++k)
            {
                for (int l = j; l < j+B; ++l)
                {
                    /* independent calculations */
                    int d = l*dim + k;
                    int s = k*dim + l;
                    if (s < limit && d < limit)
                    {
                        dst[d] = src[s]
                    }
                }
            }

        }
    }
}

6.46
技术分享图片

技术分享图片

这个题仅仅是6.45的一个实践版。但这个题有一个小技巧，就是G[d] || G[s]这个运算对于G[d]和G[s]都是一样的，所以只用计算一次，从而我们只用计算对角线的上半部分的内容，也就是第二外层循环的j不用从0而是从最外层循环的i开始。

#define B chunkdatas_length_of_side
void faster_col_convert(int *G, int dim)
{
    long limit = dim * dim;
    for (int i = 0; i < dim; i += B)
    {
        for (int j = i; j < dim; j += B)
        {
            /* Using blocking to improve temporal locality */

            for (int k = i; k < i+B; ++k)
            {
                for (int l = j; l < j+B; ++l)
                {
                    /* independent calculations */
                    int d = l*dim + k;
                    int s = k*dim + l;
                    if (s < limit && d < limit)
                    {
                        _Bool temp = G[d] || G[s];
                        G[d] = temp;
                        G[s] = temp;
                    }
                }
            }

        }
    }
}

# 2017-2018-1 20155337《信息安全系统设计基础》第十三周学习总结

标签：temporary   read   block   版本   cache   int   oid   ons   body   

原文地址：http://www.cnblogs.com/Twe1vE/p/8052582.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！