2017-2018-1 20155308 《信息安全系统设计基础》第13周学习总结
一、教材学习内容详细总结
存储器系统是一个具有不同容量、成本和访问时间的存储设备的结构。
存储技术
随机访问存储器
- 随机访问存储器分为两类:静态RAM(SRAM)和动态RAM(DRAM)。
- 静态RAM: SRAM将每个位存储在一个双稳态的存储器单元里,每个单元是用一个六晶体管电路来实现的。
- 动态RAM: 每一位的存储是对一个电容的充电,电容约为30×10-15F;对干扰非常敏感,当电容的电压被扰乱之后,它就永远不会恢复了。暴露在光线下会导致电容电压改变。
SRAM和DRAM的区别:
只要有电,SRAM就会保持不变,而DRAM需要不断刷新;
SRAM比DRAM快;
SRAM对光和电噪声等干扰不敏感;
SRAM比DRAM需要使用更多的晶体管,所以更昂贵。
- 传统的DRAM:
DRAM芯片中的单元被分成d个超单元,meige超单元都由w个DRAM单元组成,一个d*w的DRAM总共存储了dw位信息。超单元被组织成一个r行c列的长方形阵列,这里rc=d.每个超单元有形如(i,j)的地址,这里i表示行,j表示列。 - 内存模块
- 增强的DRAM:
- 快页模式:异步控制信号,允许对同一行连续的访问可以直接从行缓冲区得到服务。
- 扩展数据输出:异步控制信号,允许单独的CAS信号在时间上靠的更紧密一点
- 同步
- 双倍数据速率同步:使用两个时钟沿作为控制信号,使DRAM速度翻倍。
- 非易失性存储器:即使在关电之后,仍然保存信息。
- 访问主存:
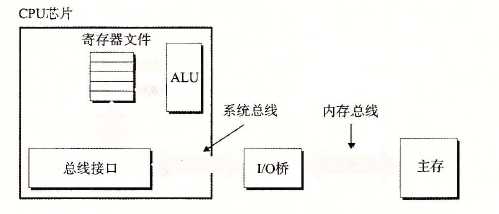
磁盘存储
- 磁盘构造: 由盘片构成,每个盘片有两面或者称为表面,表面覆盖着磁性记录材料。盘片中央有一个可以旋转的主轴,使得盘片以固定的旋转速率旋转,通常是5400~15000转每分钟(RPM)
- 磁盘容量: 一个磁盘上可以记录的最大位数称为它的最大容量/容量。
- 计算磁盘容量的公式:

- 磁盘操作:磁盘用读写头来读写存储在磁性表面的位,而读写头连接到一个转动臂一端。
- 磁盘以扇区大小的块来读写数据。对扇区的访问时间有三个主要部分:寻道时间、旋转时间和传送时间。
- 寻道时间:移动传送臂所需要的时间
- 旋转时间:一旦读写头定位你到了期望的磁道,驱动器等待目标扇区的第一个位旋转到读写头下。 该性能依赖于当读写头到达目标磁道时盘面的位置和磁盘的旋转速度。最大旋转延迟
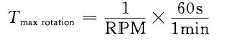
- 传送时间:一个扇区的传送时间依赖于旋转速度和每条磁道的扇区数目。平均传送时间
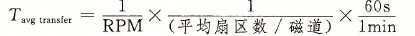
一个磁盘扇区内容的平均时间为平均寻道时间、平均旋转延迟和平均传送时间之和。
- 逻辑磁盘块:
三元组(盘面,磁道,扇区):唯一地表示了对应的物理扇区。 - 连接到I/O设备:
- 通用串行总线(USB)
- 图形卡(适配器)
- 主机总线适配器
- 访问磁盘:
读一个磁盘扇区:
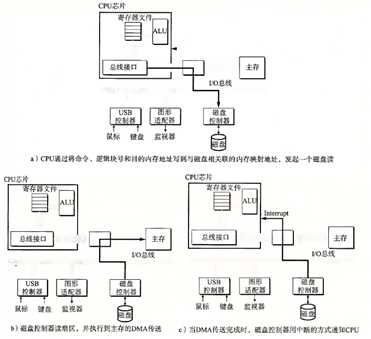
固态磁盘
固态硬盘是一种基于闪存的存储技术。
- 优点:由半导体构成,没有移动的部件;随机访问时间比旋转磁盘要快、能耗低、结实。
- 缺点:易磨损、更贵
局部性
- 局部性:倾向于引用邻近与其他最近引用过的数据项的数据项,或者最近引用过的数据项本身,这种倾向性,被称为局部性原理。
- 局部性包括时间局部性和空间局部
时间局部性:被引用过一次的存储器位置很可能在不远的将来再被多次引用。
空间局部性:一个存储器位置被引用了一次,那么程序很可能在不远的将来引用附近的一个存储器位置。
对程序数据引用的局部性
一个向量的元素是被顺序读取,因此函数具有很好的空间局部性,但是每个向量元素只被访问依次,因此空间局部性很差。
取指令的局部性
代码区别于程序数据的一个重要属性是在运行时它是不能被修改的。当程序正在执行时,CPU只从存储器中读出它的指令,CPU绝不会重写或修改这些指令。
练习

答:
int sumarry3d(int a[N][N][N])
{
int i,j,k,sum = 0;
for(k=0;k<n;k++){
for(i=0;i<N;i++) {
for(j=0;j<N;j++){
sum+=a[k][i][j];
}
}
}
}存储器层次结构
- 存储技术:不同的存储技术的访问时间差异很大,速度较快的技术每字节的成本要比速度较慢的技术高,而且容量较小,CPU和主存之间的速度差距在增大。
- 计算机软件:一个编写良好的程序倾向于展示出良好的局部性。
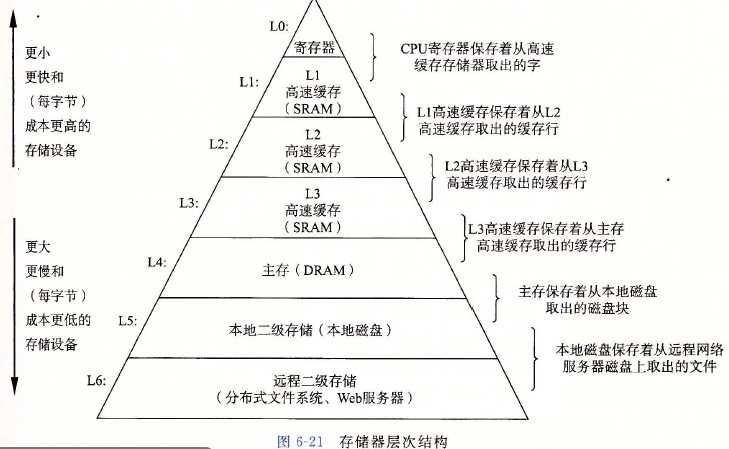
存储器层次结构中的缓存
- 高速缓存:是一个小而快速地存储设备,它作为存储在更大、也更慢的设备中的数据对象的缓冲区域。
- 缓存命中:当程序需要第k+1层的某个数据对象d时,首先在当前存储在第k层的一个块中查找d,如果d刚好缓存在第k层中,就称为缓存命中。
- 缓存不命中:第k层中没有缓存数据对象d
- 缓存不命中的种类:
- 强制性不命中/冷不命中:即第k层的缓存是空的(称为冷缓存),对任何数据对象的访问都不会命中。通常是短暂事件,不会在反复访问存储器使得缓存暖身之后的稳定状态中出现。
- 冲突不命中:将第k+1层的某个块限制放置在第k层块的一个小的子集中,这就会导致缓存没有满,但是那个对应的块满了,就会不命中。
- 容量不命中:当工作集的大小超过缓存的大小时,缓存会经历容量不命中,就是说缓存太小了,不能处理这个工作集。
- 缓存管理:某种形式的逻辑必须管理缓存,而管理缓存的逻辑可以是硬件、软件,或者两者的集合。
高速缓存存储器
存储器层次结构只有三层:CPU寄存器、DRAM主存储器和磁盘存储。
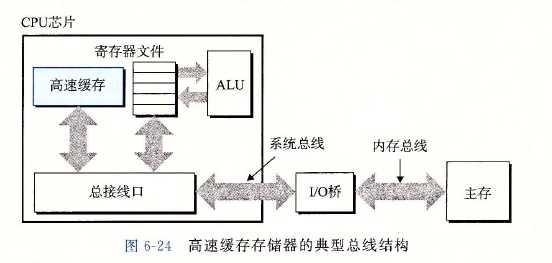
通用的高速缓存存储器结构
- 每个存储器地址有m位,形成M=2^m个不同的地址。
- 高速缓存组:S = 2^m个高速缓存组的数组,每个组包括E个高速缓存行:B = 2^m字节的数据块组成。有效位指明这个行是否包含有意义的信息。还有t = m -(b+s)标记位唯一地标识存储在这个高速缓存行中的块。
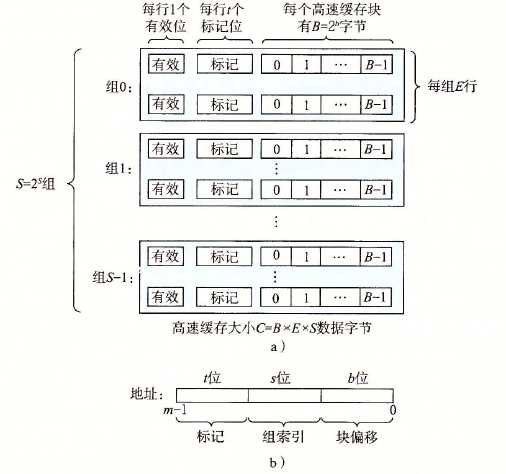
直接映射高速缓存
直接映射高速缓存:每个组只有一行的高速缓存。
高速缓存确定一个请求是否命中,然后抽取出被请求的字的过程,分为三步:(1)组选择(2)行匹配(3)字抽取
- 组选择: ?高速缓存从w的地址中间抽取出s个组索引位
- 组索引位:一个对应于一个组号的无符号整数。
- 行匹配: ?判断缓存命中的两个充分必要条件:该行设置了有效位;高速缓存行中的标记和w的地址中的标记相匹配
- 字选择:确定所需要的字在块中是从哪里开始的。
组相联高速缓存
- 组选择:与直接映射高速缓存中的组选择一样,组索引位标识组。
- 行匹配和字选择:把每个组看做一个小的相关联存储器,是一个(key,value)对的数组,以key为输入,返回对应数组中的value值。高速缓存必须搜索组中的每一行,寻找有效的行其标记与地址中的相匹配。形式是(key, value),用key作为标记和有效位去匹配,匹配上了之后返回value。
- 组相连高速缓存中不命中时的行替换:
- 最不常使用策略LFU:替换在过去某个时间窗口内引用次数最少的那一行。
- 最近最少使用策略LRU:替换最后一次访问时间最久远的那一行。
全组相连高速缓存:
- 组选择:只有一个组,没有组索引位。
- 行匹配和字选择:与组相连高速缓存是一样的,但规模大很多,因此只适合做小的高速缓存。
有关写的问题
- 处理写命中时:
-直写:立即将w的高速缓存块协会到紧接着的低一层中;缺点:每次写都会引起总线流量。 - 写回:只有当替换算法要驱逐更新过的块时,才写到紧接着的低一层中。优点:符合局部性原理,显著的减少总线流量;缺点:增加了复杂性,必须为每个高速缓存行维护一个额外的修改位
处理写不命中的处理方法:
- 写分配(对应写回):加载相应的低一层中的块到高速缓存中,然后更新这个高速缓存块。
- 非写分配(对应直写):避开高速缓存,直接把这个字写在低一层中。
高速缓存参数的性能影响
- 高速缓存大小的影响
- 块大小的影响
- 相联度的影响
- 写策略的影响
家庭作业中重点问题及解决过程
- 问题一:

解决过程:
cache共有256个block,分别位于256个set中,每个block可以放下4个int类型的变量,所有的block可以放下1024个int类型的变量。
当N = 64:
映射关系:a[0][0] ~ a[15][63]、a[16][0] ~ a[31][63]、a[32][0] ~ a[47][63]、a[48][0] ~ a[63][63] 互相重叠。
sumA按照行来读取,所以每四次读取第一次都会miss,即miss rate = 25%。
sumB按照列来读取,所以每一次读取都会发生miss(读取后的block又会被覆盖),即miss rate = 100%。
sumC按照列来读取,但是每次读取后都会按照行再读取一次,所以每四次读取会有两次miss,即miss rate = 50%。
当N = 60
映射关系:a[0][0] ~ a[17][3]、a[17][4] ~ a[34][7]、a[34][8] ~ a[51][11]、a[51][12] ~ a[59][59]互相重叠,其中最后的a[51][12] ~ a[59][59]没有到达cache的尾部。
sumA按照行来读取,所以每四次读取第一次都会miss,即miss rate = 25%。
sumB按照列来读取,这里的情况有些复杂,我写了一个程序来分析:
#include <stdio.h>
#define SIZEOFCACHE 256
#define SIZEOFBLOCK 4
#define N 60
int main()
{
int cache[SIZEOFCACHE];
for (int k = 0; k < SIZEOFCACHE; ++k)
{
cache[k] = -1;
}
int read = 0;
int miss = 0;
for (int j = 0; j < N; ++j)
{
for (int i = 0; i < N; ++i)
{
//read a[i][j]
++read;
int position = i * N + j;
int need_start = position/SIZEOFBLOCK;
if (cache[need_start%SIZEOFCACHE] != need_start)
{
++miss;
cache[need_start%SIZEOFCACHE] = need_start;
}
}
}
printf("%g\n", miss/(double)read);
return 0;、
}输出结果为25%。
C.
将上面程序的循环部分更改为:
for (int j = 0; j < N; j+=2)
{
for (int i = 0; i < N; i+=2)
{
//read a[i][j] a[i+1][j] a[i][j+1] a[i+1][j+1]
++read;
int position = i * N + j;
int need_start = position/SIZEOFBLOCK;
if (cache[need_start%SIZEOFCACHE] != need_start)
{
++miss;
cache[need_start%SIZEOFCACHE] = need_start;
}
++read;
position = (i+1) * N + j;
need_start = position/SIZEOFBLOCK;
if (cache[need_start%SIZEOFCACHE] != need_start)
{
++miss;
cache[need_start%SIZEOFCACHE] = need_start;
}
++read;
position = i * N + j + 1;
need_start = position/SIZEOFBLOCK;
if (cache[need_start%SIZEOFCACHE] != need_start)
{
++miss;
cache[need_start%SIZEOFCACHE] = need_start;
}
++read;
position = (i+1) * N + j + 1;
need_start = position/SIZEOFBLOCK;
if (cache[need_start%SIZEOFCACHE] != need_start)
{
++miss;
cache[need_start%SIZEOFCACHE] = need_start;
}
}
}输出结果为25%。
- 问题二

答:
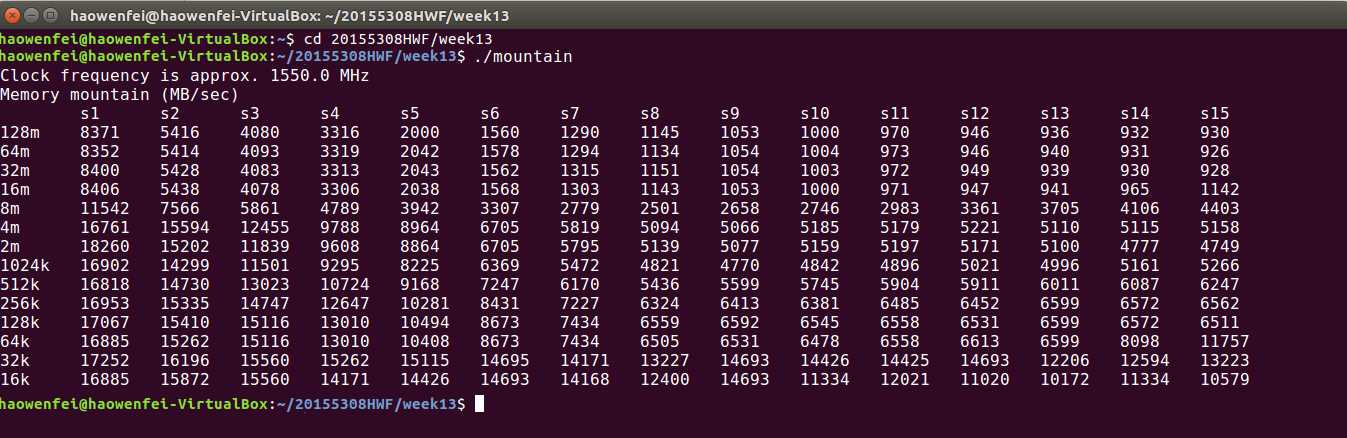
- 问题三:

答:
void transpose(int *dst, int *src, int dim)
{
int i, j;
for (i = 0; i < dim; ++i)
{
for (j = 0; j < dim; ++j)
{
dst[j*dim + i] = src[i*dim +j] /* ! */
}
}
}以上的关键语句中的乘法和加法已经实现了循环之间独立,src也是按照行读入的,但是dst却是按照列读入的,这样没有充分利用每一次读入的block。于是我们想到可不可以每一次读入dst[j*dim + i]所在的block之后继续写入例如dst[j*dim + i + 1] dst[j*dim + i + 2]这样的变量,但是这样有需要src的部分变为src[(i+1)*dim +j]等等,所以我们现在不仅要“横向”扩展dst,还要“纵向”扩展src,其实这是一种叫做blocking的技术,即每次读入一块数据,对此块数据完全利用后抛弃,然后读取下一个块。可以参考csapp网上给的注解:MEM:BLOCKING — Using blocking to increase temporal locality
设我们的数据块的宽度是B,由于我们要对两个数组进行读写操作,所以2B^2 < C(其中C是cache的容量),在此限制下B尽可能取大。
#define B chunkdatas_length_of_side
void faster_transpose(int *dst, int *src, int dim)
{
long limit = dim * dim;
for (int i = 0; i < dim; i += B)
{
for (int j = 0; j < dim; j += B)
{
/* Using blocking to improve temporal locality */
for (int k = i; k < i+B; ++k)
{
for (int l = j; l < j+B; ++l)
{
/* independent calculations */
int d = l*dim + k;
int s = k*dim + l;
if (s < limit && d < limit)
{
dst[d] = src[s]
}
}
}
}
}
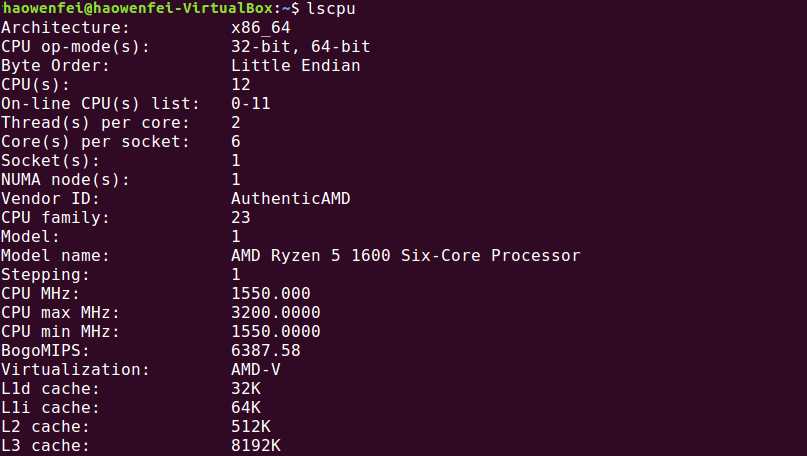
}用lscpu验证分析正确:
- 问题四:


答:
#define B chunkdatas_length_of_side
void faster_col_convert(int *G, int dim)
{
long limit = dim * dim;
for (int i = 0; i < dim; i += B)
{
for (int j = i; j < dim; j += B)
{
/* Using blocking to improve temporal locality */
for (int k = i; k < i+B; ++k)
{
for (int l = j; l < j+B; ++l)
{
/* independent calculations */
int d = l*dim + k;
int s = k*dim + l;
if (s < limit && d < limit)
{
_Bool temp = G[d] || G[s];
G[d] = temp;
G[s] = temp;
}
}
}
}
}
}