最小二乘法可以从Cost/Loss function角度去想,这是统计(机器)学习里面一个重要概念,一般建立模型就是让loss function最小,而最小二乘法可以认为是 loss function = (y_hat -y )^2的一个特例,类似的像各位说的还可以用各种距离度量来作为loss function而不仅仅是欧氏距离。所以loss function可以说是一种更一般化的说法。
最大似然估计是从概率角度来想这个问题,直观理解,似然函数在给定参数的条件下就是观测到一组数据realization的概率(或者概率密度)。最大似然函数的思想就是什么样的参数才能使我们观测到目前这组数据的概率是最大的。
类似的从概率角度想的估计量还有矩估计(moment estimation)。就是通过一阶矩 二阶矩等列方程,来反解出参数。
有人提到了正态分布。最大似然估计和最小二乘法还有一大区别就是,最大似然估计是需要有分布假设的,属于参数统计,如果连分布函数都不知道,又怎么能列出似然函数呢? 而最小二乘法则没有这个假设。 二者的相同之处是都把估计问题变成了最优化问题。但是最小二乘法是一个凸优化问题,最大似然估计不一定是。
注:
从优化的角度上来讲,负的log likelihood 就是求MLE(最大似然估计)要优化的目标函数。
那么为啥MLE需要设置分布这么麻烦,还有这么多应用,因为当likelihood设置正确的时候,这个目标函数给出的解最efficient。
那么为啥有这么多人把MLE和LOSE搞混,因为当likelihood用的是gaussian的时候,由于gaussian kernel里有个类似于Euclidean distance的东西,一求log就变成square loss了,导致解和OLSE是一样的。而碰巧刚接触MLE的时候基本都是gaussian假设,这才导致很多人分不清楚。
从概率论的角度:
Least Square 的解析解可以用 Gaussian 分布以及最大似然估计求得
Ridge 回归可以用 Gaussian 分布和最大后验估计解释
LASSO 回归可以用 Laplace 分布和最大后验估计解释
-------------------------------------------------------------------
下面是上述三种的推导
注意:
首先知道什么是:高斯分布、拉普拉斯分布、最大似然估计,最大后验估计(MAP)。
按照李航博士的观点,机器学习三要素为:模型、策略、算法。
一种模型可以有多种求解策略,每一种求解策略可能最终又有多种计算方法。
以下只推导模型策略,不讲算法。


区别:
最大似然估计不考虑先验后验的问题,纯粹是选择一个参数能最大化模型似然度
最大后验概率是贝叶斯方法,引入参数的先验概率,结合似然度选择最佳参数或模型

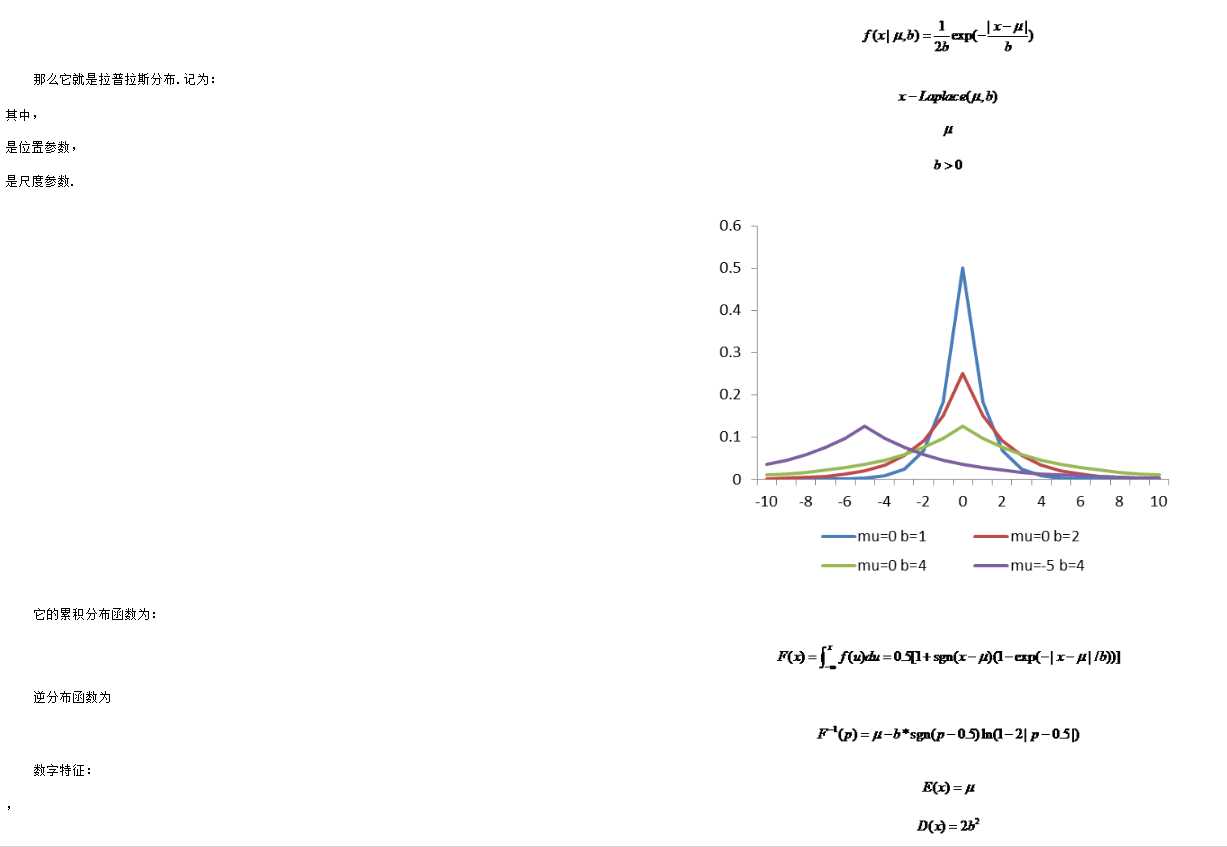
拉普拉斯分布
-
在概率论与统计学中,拉普拉斯分布是以皮埃尔-西蒙·拉普拉斯的名字命名的一种连续概率分布.由于它可以看作是两个不同位置的指数分布背靠背拼接在一起,所以它也叫作双指数分布.两个相互独立同概率分布指数随机变量之间的差别是按照指数分布的随机时间布朗运动,所以它遵循拉普拉斯分布.
如果随机变量的概率密度函数为