量子逻辑的光学模拟(PRA, 1998) 主机中《1998Cerf.pdf》
核心:
1. 用一个光子的多条路径的叠加态来表示n qubits, 那么实验上干涉仪所包含的路径数为 2^n
2. 实现量子门(or conditional dynamics): 在各路径上使用不同光学元素。比如一个 50:50 BS 相当于一个sqrtm(NOT) gate for an input qubit, 即output 为路径自由度的叠加态;一个 phase shifter act as a quantum phase gate.
3. Fig 1 中的(b)(c) 已用到了路径和极化这2个自由度,也是日后各种多自由度光子实验的雏形。
方法:使用线性光学器件来模拟小规模量子线路。
根据:用单光子表示几个量子bits, 使用简单的光学零件(BS,phase shifter 等)来执行普适量子门。
意味着:小量子网络的光学实现是合理的目标。
例子:呈现了非平凡 3-bit quantum circuit 的光学模拟。
U(N)中的每一个矩阵都可以使用一批O(N^2)个BS来构建,它们组成 a optical multiport with N input and N output beams.
这篇文献,我们讨论了‘ 量子网络’ 和‘ 线性光学装置’ 的一种对应。
实现:引入 a single-photon 来表示几个qubit, 这建立在传统线性光学元素(如BS or phase shifters)和one-bit 量子门的等价性。
例如:
量子线路术语中,一个‘ 光学对称BS ’ 行为为一个量子√NOT 门(up to a phase of pi/4), 如果我们使用一对儿输入模式 |01> (or |10>) 来表示 qubit 的逻辑 0(1) 态。如果一个输入端口为处于真空态 |0>, 且第二个输入端口处于单光子态 |1>, 那么 2 个输出端口实际上处于叠加态 |01>+i |10>.
类似地,使用一个phase shifter 作用到光子的一个模式上可以获得一个量子相门。
换而言之,单光子干涉仪实验可以用量子线路语言阐述,the ‘which-path‘ 变量被替换为一个 qubit.
前人的工作中:‘量子逻辑‘ 和‘ 单光子光学实验’ 之间的二元性(duality)还没有被利用。
这里,我们利用了一个事实:n qubits 可以被处于本质上包含 2^n 条路径的干涉仪装置中的一个光子来表示,这样通过使用不同路径中的不同光学元素可以执行量子条件动力学。
下图(a)Hadamard gate on a ‘location‘ qubit
(b) CNOT门,使用极化旋转器。control qubit: location; target qubit: polarization
(c) CNOT门。 control qubit: polarization ; target qubit: location
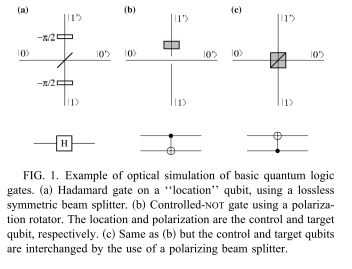
我们这里的模型以一种直接的方式将任何 n-bit 量子线路翻译为一个单光子光学装置,只要 n 不太大。
要付出的代价:
1. 光路数的指数增长; 2. 导致所要求光学器件的增长。
