摘要:
- 元胞自动机能利用简单的局部规则和离散方法描述复杂的全局的连续系统,已成为探索复杂系统的一种有效工具。
- 文章
- 阐述了元胞自动机的发展历程、结构、特征及基本理论与方珐;
- 介绍了元胞自动机在寡头垄断行为、交通管理及工程运输、城市发展、市场营销、股票投资、企业战略等管理领域中的应用;
- 指出元胞自动机理论的优势与不足,
- 并提出进一步的研究展望。
1引言
复杂科学
- 20世纪80年代,以美国圣塔菲(SantaFe)学派为首提出了复杂科学,一经提出,在世界范围内引起了广泛的关注。目前,关于复杂性和复杂系统的科学研究占据着越来越重要的位置,以至于被有些科学家誉为“21世纪的科学”。
- 1985年,耗散结构理论的创始人,诺贝尔化学奖获得者I.Prigogine提出了社会经济复杂系统中的自组织问题。1988年,诺贝尔物理学奖获得者P.Anderson和诺贝尔经济学奖获得者K.J.Arow通过组织专题讨论会,提出了经济管理可以看作是一个演化着的复杂系统。此后,随着研究的不断深入,复杂系统中所涉及的非线性、非平衡、突变、混沌、分形、自组织等理论在经济管理领域有了越来越广泛的应用。
元胞自动机
- 在复杂性和复杂系统的研究过程中,国内外学者提出了许多探索复杂性的方法及工具,其中,元胞自动机(cellularautomaton,CA)以其组成单元的简单规则性,单元之间作用的局部性和信息处理的高度并行性,并表现出复杂的全局性等特点而备受关注,成为探索复杂系统的一种有效工具。
2元胞自动机的基本理论及方法
2.1元胞自动机的发展
- 20世纪50年代初,现代计算机的创始人冯·诺依曼(vonNeuman)为模拟生物发育中细胞的自我复制而提出了元胞自动机的雏形。但在当时这项工作并未引起广泛的关注与重视。
- 1970年,剑桥大学的J.H.Conway设计了一种计算机游戏———“生命的游戏”。它是具有产生动态图案和动态结构能力的元胞自动机模型,吸引了众多科学家的兴趣,推动了元胞自动机研究的迅速发展。
- 之后,S.Wolfram对初等元胞自动机的256种规则产生的所有模型进行了详细而深入的研究。他还用熵来描述其演化行为,把元胞自动机分为:平稳型、周期型、混沌型、复杂型四类。
- 近年来随着复杂性研究的进展,作为探索复杂系统的一种有效工具,元胞自动机获得了深入的研究和广泛的应用。
2.2元胞自动机的构成特征
2.2.1元胞自动机的构成
标准元胞自动机是一个由「元胞、元胞状态、邻域和状态更新规则」构成的四元组,用数学符号可以表示为A=(L,d,S,N,f)
- A代表一个元胞自动机系统
- L表示元胞空间
- d表示元胞自动机内元胞空间的维数,是一正整数
- S是元胞有限的、离散的状态集合
- N表示某个邻域内所有元胞的集合
- f表示局部映射或局部规则。
具体描述:
- 元胞空间
- 元胞是构成元胞自动机的最基本单元,而元胞空间是元胞所分布的空间网点集合。
- 理论上,元胞空间是在各维向上无限延展的,但实际中无法在计算机上实现。因此,需要定义不同的边界条件。
- 元胞空间的边界条件主要有三种类型:周期型、反射型和定值型。
- 元胞状态
- 通常在某一个时刻一个元胞只能有一种元胞状态,而且该状态取自一个有限集合,如{0,1},{生,死}或{0,a1,a2,an}。
- 在社会科学领域中,元胞状态可以用来代表个体所持的态度、个体特征或行为等。
- 邻域
- 在空间位置上与元胞相邻的细胞称为它的邻元,由所有邻元组成的区域称为它的邻域。
- 在一维元胞自动机中,通常以半径r来确定邻域,距离某个元胞r内的所有元胞均被认为是该元胞的邻域。
- 一维元胞自动机的邻域:
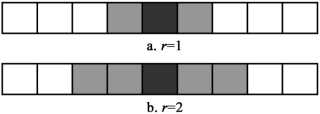 ?
?
- 在二维元胞自动机中,通常有以下几种类型的邻域:
- 冯·诺依曼型(vonNeumanNeighborhoods)
- 摩尔型(MooreNeighborhoods)
- 马哥勒斯型(MargolusNeighborhoods)
- 它是每次将一个2×2的元胞块做统一处理,而上述前两类邻域中,每个元胞是分别处理的
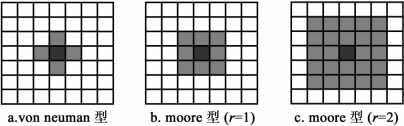 ?
?
- 同样,也可以定义二维以上的高维元胞自动机的邻域
- 状态更新规则
- 是指根据元胞当前状态及其邻域中元胞的状态决定下一时刻该元胞状态的状态转移函数。
- 状态更新规则可以写为
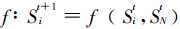 ?,
?,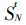 ?为t时刻的邻域状态组合,称为元胞自动机的局部映射或局部规则。
?为t时刻的邻域状态组合,称为元胞自动机的局部映射或局部规则。
2.2.2标准元胞自动机的特征
- 离散性:元胞自动机的空间、时间及状态都是离散的。
- 同质性:元胞空间中每个单元格可能具有的状态集合相同,并且决定各个元胞状态变化的规则也是相同的。
- 并行性:元胞空间中各个元胞按状态更新规则变化是同步进行的,特别适合于并行计算,且各个元胞的状态变化是独立行为,互相没有任何影响。
- 局部性:一个元胞在t+1时刻的状态由其周围半径为r的邻域中的元胞的当前时刻t的状态决定,因此,在时间、空间上都存在着局部性。
- 维数高:元胞自动机是一类无穷维动力系统。
3元胞自动机在管理系统中的应用
元胞自动机已被广泛地应用于社会、经济、军事以及自然科学的各个领域
- 在社会学中,元胞自动机用于研究政治组织的突现、个人行为的社会性、流言的传播等。
- 在生物学中,用于肿瘤细胞的增长机理和过程模拟、人类大脑的机理探索、艾滋病病毒HIV的感染过程、自组织、自繁殖等生命现象的研究以及克隆技术的研究。
- 在计算机科学中,元胞自动机被视为并行计算机而用于并行计算的研究。
- 在物理学中,除了格子气元胞自动机在流体力学上的成功应用,元胞自动机还应用于磁场、电场等场的模拟,以及热扩散、热传导和机械波的模拟。
- 在军事科学中,元胞自动机用于模拟军事作战,理解战争过程。
- 在管理领域,国内外学者开始应用元胞自动机来解释分析各种管理现象,对各种管理现象进行演化模拟。
元胞自动机在管理系统中的应用: ?
?
4标准元胞自动机的优势与不足
从复杂系统的研究不难看出,应用元胞自动机方法对复杂系统进行描述具有很多优势:
- 元胞自动机方法是立足于复杂系统的特征去模拟和描述复杂性的,因而更具有针对性、典型性和准确性。元胞自动机方法的基本出发点有三个方面:
- 复杂系统是由许多基本单元组成的
- 每个基本单元的状态为有限的几种
- 每一基本单元的状态随时间的演化只取决于相邻单元的状态
- 元胞自动机采用典型的“自下而上”的建模方法,符合复杂系统的形成规律,也是大多数复杂系统研究采用的思维方式,是复杂科学所倡导的复杂性研究方法。
- 元胞自动机的离散性使许多复杂问题得以简化,其统计测度也很容易计算,易于完成从概念模型到计算机物理模型的转变。
- 元胞自动机方法是用元胞作为基本单元描述复杂系统的整体行为,演化的规则可以预设,许多过程可以通过计算机来完成,所以具有直观性及可控性。
- 元胞自动机方法可以使微观层面上决策和机制如何产生一定的动态宏观效果的过程更加明晰和易于掌握。
- 元胞自动机方法以新的设定表征了复杂系统“确定性中的内在随机性”,即应用元胞的设定和确定的规则最终使系统产生随机结果。在加一定的随机项之后又使系统产生确定性结果,体现了随机性与确定性两者结合的非线性系统的基本特征。
- 元胞自动机中的状态更新规则不依赖于数学函数,甚至可用语言简单描述亦可达到相同目的,因此元胞自动机模型的表达更为直观、简单。
- 元胞自动机具有应用的广泛性、灵活性和开放性。元胞自动机不是一种数理方程,而是一种方法框架。
- 一方面,各领域的学者通过扩展元胞自动机的组成构件,提出和建立适合专题现象的扩展模式;
- 另一方面,元胞自动机允许建模者在模型框架下,用各领域的专业规律构建状态更新规则,灵活地结合已有的相关专业模型,使得元胞自动机具有应用的广泛性、灵活性和开放性。
标准元胞自动机模型也存在一些缺陷和不足:
- 元胞形态
- 在标准元胞自动机中,元胞具备规则一致的形状,有规律地在元胞空间中排列。但是在现实世界中很少有如此规则的状态。
- 元胞空间的几何形状
- 在标准元胞自动机中,二维元胞空间可按照三角形、四边形、六边形等几种网格排列。
- 三角形网格的缺点是在计算机显示与表达时困难,须转变成四方网格。
- 但四方网格缺点是不能较好地模拟各向同性现象。
- 六边形网格的能较好地模拟各向同性现象,模型更加自然而真实,但是表达和显示上较困难、复杂。
- 元胞邻域的定义
- 在标准元胞自动机中,邻域的定义也较严格:
- 在一维元胞自动机中通常以半径r来确定邻域,在距离某个元胞r内的所有元胞被认为是该元胞的邻域。
- 二维元胞自动机通常以规则的空间单元划分,按照vonNeuman型、Moore型和Margolus型等方法进行处理。
- 这直接导致元胞状态更新规则不能应用于更远的单元。
- 在标准元胞自动机中,邻域的定义也较严格:
- 元胞状态更新规则的确定,在标准元胞自动机的状态更新规则中:
- 规则中的因素过于单一
- 元胞状态变化仅取决于邻域的状态组合,因此状态变量既是自变量又是因变量。
- 而实际上,一个系统元素的行为不仅取决于一个层面的变量,其受制因素是大量的。
- 没有考虑宏观作用因素
- 但系统要素的行为不仅仅取决于自身及邻域的局部小环境,而且还受到系统大环境的影响
- 状态更新规则往往是确定的,但在实际复杂系统中,系统元素的行为往往是随机的,表现出某种倾向性和可能性
- 状态更新规则的定义较难,合理的更新规则是自动机模型效果的关键。
- 规则是针对抽象空间划分的单元,发生在单元间的局部相互作用。
- 这个局部规则与宏观规律既有联系又有差别,其定义又是靠直觉和经验,因而找到与实际规律相符的映射函数难度相当大
- 设计不当的状态更新规则会产生一些人为制造的错误后果。
- 规则中的因素过于单一
值得注意的是,以上标准元胞自动机的不足目前已经逐步得到改进,因此元胞自动机应用模型大多数已不再是标准元胞自动机模型。但对于标准元胞自动机的改进还有待于进一步提高,以提高元胞自动机对现实世界的模拟和应用能力。
5研究展望
元胞自动机具有利用简单的局部的规则和离散的方法描述复杂的全局的连续系统的能力,因此,元胞自动机不仅在自己的领域而且在科学研究的方法学上对许多相关领域产生巨大影响。
元胞自动机研究与应用的主要发展趋势将有如下几个方面:
- 应用范围将进一步扩大。
- 从元胞自动机在自然科学领域及社会科学领域的应用,尤其是在管理系统中的应用,可以预见元胞自动机具有广阔的应用前景。如在交通运输工程、环境工程等各管理系统中的应用将会不断扩大。
- 研究深度将不断加强。
- 目前,元胞自动机的理论与方法研究在我国还处于介绍国外研究成果、进行初步研究的时期,国内许多学者正在各自的领域推进元胞自动机及其应用的研究。在管理系统的元胞自动机的研究中,一方面需要对已有的模型进行更深入的探讨;另一方面,需要以元胞自动机理论为基础建立新的模型,同时也要注意吸收国外的最新研究成果,借鉴其他学科元胞自动机研究的主要成果。总之,元胞自动机的研究深度有待不断加强。
- 标准模型将不断扩展。
- 由于标准元胞自动机的缺陷及局限性,国内外学者从不同方面对标准元胞自动机进行了扩展,如连续型的元胞自动机,多维状态空间元胞自动机,多层级元胞自动机,多元随机的元胞自动机以在本文所提到的管理系统应用中对标准元胞自动机各构成要素的扩展等等。随着元胞自动机研究的不断深入和应用范围的不断扩大,标准元胞自动机必将被不断扩展,使得元胞自动机对真实世界的模拟和应用能力不断加强。
- 其他方法将不断被引入元胞自动机模型中。
- 随着研究的深入,其他领域的一些方法将不断地被引入元胞自动机模型。如将遗传算法和元胞自动机集成,使状态更新规则具有遗传性,形成遗传自动机;将状态更新规则模糊化,则可以有模糊规则,形成模糊元胞自动机;元胞的状态可以根据神经网络的阈值函数来更新,形成神经元胞自动机等。因此,元胞自动机与其他方法的不断结合将使元胞自动机的功能越来越强大,成为一种研究复杂系统的越来越有效的方法与工具。
参考文献
- 本文修改自:《中国工程科学》第9卷第一期《元胞自动机:一种探索管理系统复杂性的有效工具》,福州大学管理学院陈国宏
- 本文地址:http://www.cnblogs.com/bellkosmos/p/introduction_of_cellular_automata.html
