坑了好久,本来打算就这样弃着,最近又被神秘力量驱使来学这个东西,过程很痛苦但最终还是知道它到底是啥了
它可以用来对森林进行各种操作,为了快速地实现各种操作,我们要像树剖一样把整个森林剖成许多条链,每条链都用splay维护
为了在splay中体现链中节点的相对顺序,splay以节点深度为关键字(从小到大)
不同链之间的连接通过splay根节点的父亲来体现
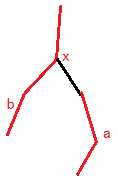
如图中所示,假设链$a$的splay根节点为$p$,链$b$中的节点$x$与链$a$相连,那么我们让$fa_p=x$
把森林剖成这些链之后,我们需要对其进行各种操作,比如形态改变和路径信息查询
所有的操作都基于一个东西:access
access($x$),就是“访问”节点$x$
感性地理解,一般访问树中的节点都要从树根开始走,所以这个操作实际上就是把$x$到根路径上的点都弄到一棵splay里
实现不难,我们需要从$x$按照链一直往上跳,遇到非链的边就把它连到$x$所属的链上,并把涉及到的其他链适当断开
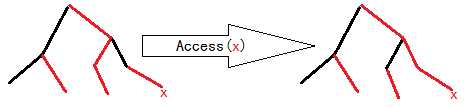
具体点,给一个真代码
void access(int x){
int y=0;
while(x){
splay(x);
ch[x][1]=y;
pushup(x);
y=x;
x=fa[x];
}
}
代码中的$y$表示当前链往下一条链的splay根节点,当执行splay($x$)后,$x$以及$x$的左子树都是$x$往上同一条链的点(因为深度$\leq dep_x$),把它连上之前的链(深度$\geq dep_x$),然后往上跳,一直到树根就ok了
如何判断一个点$u$是否为一棵splay的根?当$lson_{fa_u}\neq u$且$rson_{fa_u}\neq u$时,说明$u$是一棵splay的根节点(因为根节点的父亲指向另一条链的节点)
这样我们就完成了lct中的核心操作access,接下来用这个access随意乱搞就可以实现各种功能了
1.makeroot($x$):钦点$x$为树的根
void makert(int x){
access(x);
splay(x);
reverse(x);
}
假设原来的根为$r$,因为原来深度从小到大是$r\rightarrow x$,现在变为$x\rightarrow r$,所以深度的相对大小反了,所以需要把整棵splay区间翻转
2.link($x$,$y$):连接一条边$(x,y)$
void link(int x,int y){
makeroot(x);
fa[x]=y;
}
3.cut($x$,$y$):删除边$(x,y)$
void cut(int x,int y){
makeroot(x);
access(y);
splay(y);
fa[x]=0;
ch[y][0]=0;
pushup(y);
}
makeroot($x$)并access($y$)之后,这棵splay中就只有$x$和$y$两个节点了,断开就好
4.operate($x$,$y$):对$x\rightarrow y$这条路径做一些操作(询问,修改等)
void cut(int x,int y){
makeroot(x);
access(y);
splay(y);
//...
}
makeroot($x$)并access($y$)之后,这棵splay中只有$x\rightarrow y$路径上的点,我们可以对这棵splay做任何平衡树能做的操作
5.connected($x$,$y$):判断$x$和$y$是否在同一棵树中
bool connected(int x,int y){
if(x==y)return 1;
makeroot(x);
access(y);
splay(y);
return fa[x]!=0;
}
如果$x$和$y$在同一棵树上,那么在makeroot($x$)并access($y$)之后,$x$和$y$就在同一棵splay上了,再splay($y$),$x$就会被挤下去,即是说$fa_x\ne0$
刚接触的时候会觉得很不可理解,但认真去画一画,调一调就知道它的含义是啥了
