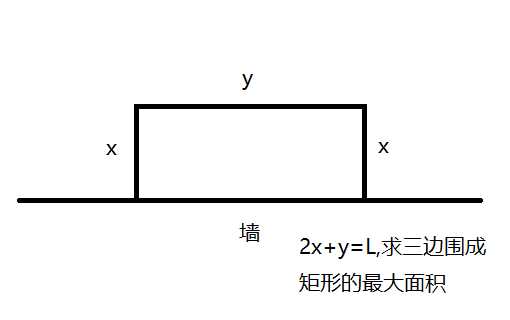
靠墙的两边设为x,墙的对边设为y,有2x+y=L;
则y=L-2x,
矩形面积函数为xy=x(L-2x)=-2x2+xL
这时就是求二次函数的极值问题了。
按二次函数y=ax2+bx+c的最值定义,当a<0时,当x=-b/2a时,有最大值ymax=(4ac-b2)/4a.(注意这一行的xy是二次函数定义里的xy,不是文中2x+y=L中的xy)
所以,当x=-b/2a=L/4时,三边围成的矩形最大面积为L2/8.
这回把初中二次方程捡起来了。
2017年12月22日
标签:sub 初中 info 多少 com 定义 bubuko http 矩形

靠墙的两边设为x,墙的对边设为y,有2x+y=L;
则y=L-2x,
矩形面积函数为xy=x(L-2x)=-2x2+xL
这时就是求二次函数的极值问题了。
按二次函数y=ax2+bx+c的最值定义,当a<0时,当x=-b/2a时,有最大值ymax=(4ac-b2)/4a.(注意这一行的xy是二次函数定义里的xy,不是文中2x+y=L中的xy)
所以,当x=-b/2a=L/4时,三边围成的矩形最大面积为L2/8.
这回把初中二次方程捡起来了。
2017年12月22日
一条长为L的绳子,一面靠墙,另外三边组成矩形,问此矩形最大面积能是多少?
标签:sub 初中 info 多少 com 定义 bubuko http 矩形
原文地址:http://www.cnblogs.com/xiandedanteng/p/8088044.html