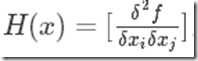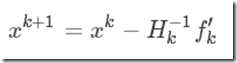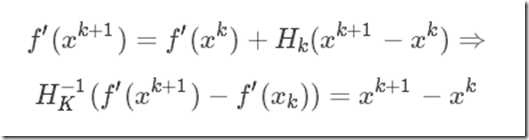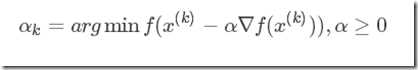拟牛顿法

拟牛顿法是求解非线性优化问题最有效的方法之一。DFP、BFGS、L-BFGS算法都是重要的拟牛顿法。

求函数的根

对f（x）在X_n附近做一阶泰勒展开

f(x)=f(X_n)+f’(X_n)(x-X_n)

假设X_n+1是该方程的根

那么就得到

X_n+1=X_n-f(X_n)/f’(X_n)

通过不断迭代从而得到真正的函数的根X*

最优化问题（牛顿法）

即是对一阶导函数求其函数的根。因此里面要涉及到求二阶导

显然这里求最优点X*的形式上与上面的求函数根的形式是一样的。

将其从低维推广至高维。则会涉及到海森矩阵H,

迭代公式变为：

我们可以看到，当Hk为正定（H_k^(-1)也为正定）的时候，可以保证牛顿法的搜索方向是向下搜索的。

牛顿法求最优值得步骤如下：

1.随机选取起始点x0

2.计算目标函数f(x)在该点xk的一阶导数和海森矩阵；

3.依据迭代公式X^k+1=X^k-H_k^(-1)f’_k

如果E(f(x_k+1)-f(x_k))＜?，则收敛返回，否则继续步骤2，3直至收敛

缺点：显然，当我们的特征特别多的时候，求海森矩阵的逆的运算量是非常大且慢的，这对于实际应用中是不可忍受的，因此我们想用一个矩阵来代替海森矩阵的逆，这就是拟牛顿法。

拟牛顿法（用一个矩阵替代海森矩阵的逆使其仍具有牛顿法的效果）

我们首先要研究一下海森矩阵需要具有什么样的特征才能保证牛顿法成功的应用。通过上面的描述我们知道

上式我们称之为拟牛顿条件。

我们所选择的替代矩阵G_k,需要满足两个条件:

1.拟牛顿条件：

2.要保证为G_k正定矩阵，这是因为只有正定才能保证牛顿的搜索方向是向下搜索

最速下降法

概念

最速下降法是梯度方法的一种实现，它的理念是在每次的迭代过程中，选取一个合适的步长α_k，使得目标函数的值能够最大程度的减小。α_k可以认为是函数?_k(α)=f(x^(k)?α?f(x^(k)))的极小值点：

概述最速下降法的过程：在每一步的迭代中，从点x^(k)出发，沿着梯度的负方向（求极小值点）展开一维搜索，直到找到步长最优值，确定新的迭代点x^(k+1)。最速下降法的相邻搜索方向都是正交的。

最速下降法的两个命题和停止条件

命题1 利用最速下降法搜索函数f:R²→R的极小值点，迭代过程产生的序列为{x^(k)}^∞_k=0, 那么，x^(k+1)?x^(k)与 x^(k+2)?x^(k+1)正交对所有k≥0都成立。

命题2 利用最速下降法搜索函数f:Rⁿ→R的极小值点，迭代过程产生的序列为{x^(k)}^∞_k=0, 如果 ?f(x^(k))≠0， 那么f(x^(k+1))<f(x^(k))。

命题1说明在迭代过程中，没产生一个新点，对应的目标函数值都会下降。命题2说明了最速下降法的下降特性：只要?f(x^(k))≠0， 就有f(x^(k+1) )<f(x^(k))。对于某个k, 如果?f(x^(k))=0，说明x(k)满足局部极小点的一阶必要条件，此时x^(k+1) =x^(k),这可以作为停止规则的基础。

常见的停止条件

参考：http://blog.csdn.net/chunyun0716