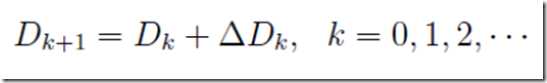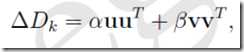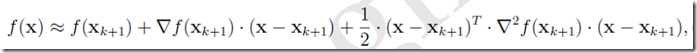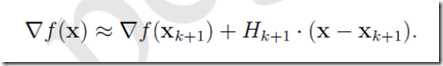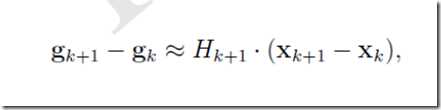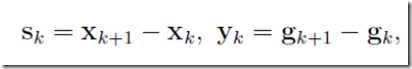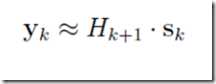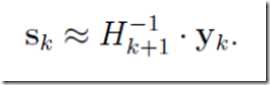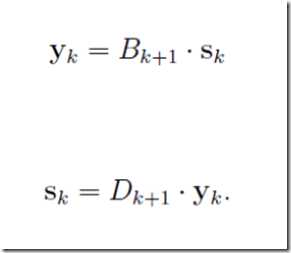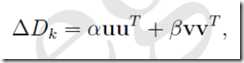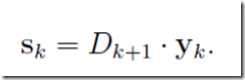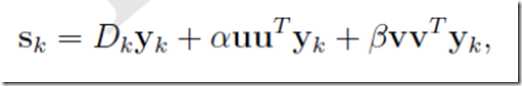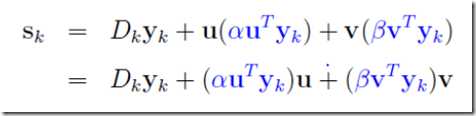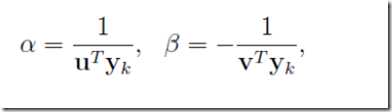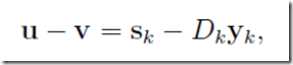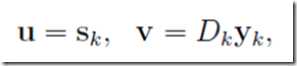DFP

该算法的核心是：通过迭代的方法，对H_k+1^(-1)近似。迭代方式：

其中D₀通常取为单位矩阵，关键是每一步构造矫正矩阵△D_k。

考虑△D_k 的待定形式为

拟牛顿的条件

这里插播一下拟牛顿的条件。

前面有讲到，拟牛顿法是想找到一个近似矩阵D来近似海森矩阵H的逆。显然D的选择是必须有条件的。为了表示清楚，下文B≈H,D≈H^-1

设经过k+1次迭代后得到X_k+1,此时将目标函数在X_k+1附近作泰勒展开，取二阶近似，得到

对其两边作用一个梯度算子▽，可得

在上式中取X=X_k,并整理得到

若引入记号

则有

或者

这就是所谓的拟牛顿条件对于我们的近似矩阵B或D则有

有了这个拟牛顿条件我们就能开始构造D了

构造矩阵D

结合两式：

则有

并且可以写成

由于和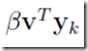是两个数，且里面α和β在里面起到类似放缩的作用，不妨假设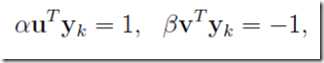

即

其中u，v仍是待定的

可以得到

不妨直接取

则有

至此则有

注：这里的（1.13）公式为

待更新！！

转自http://blog.csdn.net/itplus