瑾以此题纪念博主迈出冲刺省选的第一步
打眼一看,这不是裸的最小割吗?
最小割 == 最大流;
然后 5 分钟码完 ISAP ;
交上去一看......TLE......懵逼......
然后进行了一波没有卵用的优化常数......
(去他妈的 1e6 个点,3e6 条边!!!)
问了问度娘,才知道这题的图是 ‘平面图’ ;
平面图的最小割和最大流可以通过将其转换成对偶图跑最短路求解;(涨姿势)
那么什么是对偶图呢?
通俗的讲,对偶图就是把原图的点换成面(边围成的区域),面换成点,而无向边连接原图的面;
如下图,蓝色的是原图,红色的是对偶图,绿色的是对偶图最短路(最小环删去了s-t的边)(也是原图最小割);
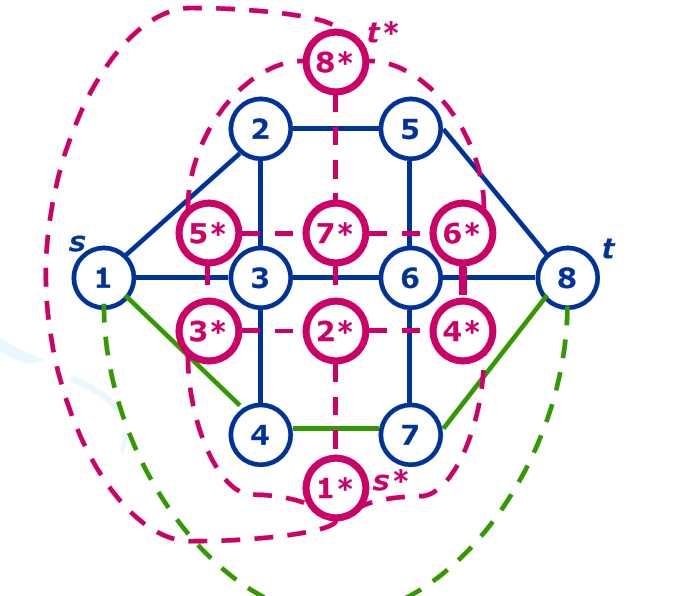
如果还不明白,请参考——周冬 Dalao《浅析最大最小定理在信息学竞赛中的应用》
注意:在平面图中,最外面还有一个无穷大的面;
然后就可以愉快的跑 SPFA 了;
所以说,有了这个 AC 这题岂不是很简单喽
No,No,No,除了搞来搞去能把你绕晕的建图之外;
本题还有一个非常非常坑的地方,没有之一!!(我查了3 Days)
那就是:
n == 1 || m ==1 啊!!(出数据的MMP)
AC 代码:
#include<bits/stdc++.h> using namespace std; int dis[2000100],used[2000100],point[6000100]; // 2e6 个点,6e6 条边... int cnt; queue<int>q; struct edge{ int u,v,next; }e[6000100]; inline int read(){ // 据说不加快读容易 TLE int x=0; char ch=getchar(); while(ch>‘9‘||ch<‘0‘) ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=(x<<3)+(x<<1)+(ch^48),ch=getchar(); return x; } inline void ad(int x,int y,int z){ e[++cnt].u=y; e[cnt].v=z; e[cnt].next=point[x]; point[x]=cnt; } inline void add(int x,int y,int z){ // 无向边 偷懒... ad(x,y,z); ad(y,x,z); } int spfa(int s,int t){ // SPFA 板子一枚 memset(dis,0x3f,sizeof(dis)); q.push(s); used[s]=1; dis[s]=0; while(!q.empty()){ s=q.front(); q.pop(); used[s]=0; for(int i=point[s];i;i=e[i].next) if(dis[e[i].u]>dis[s]+e[i].v){ dis[e[i].u]=dis[s]+e[i].v; if(!used[e[i].u]){ used[e[i].u]=1; q.push(e[i].u); } } } return dis[t]; } int main(){ int n,m,x,s=0; n=read(),m=read(); if(n==1||m==1){ // 特判很重要! s=0x3fffffff; for(int i=1;i<max(n,m);i++){ x=read(); s=min(s,x); } printf("%d\n",s); return 0; } int t=2*(n-1)*(m-1)+1; // t:终点 for(int i=1;i<=n*(m-1);i++){ x=read(); add(min(2*i,t),max(0,2*(i-m)+1),x); // 横向边 } for(int i=1;i<=(n-1)*m;i++){ x=read(); s++; if(i%m!=0&&i%m!=1) s++,add(s-1,s,x); // 纵向边 else if(i%m==0) add(s,0,x); else add(t,s,x); } for(int i=1;i<=(m-1)*(n-1);i++){ x=read(); add(2*i-1,2*i,x); // 斜向边 } printf("%d\n",spfa(0,t)); return 0; }
By The_Seventh
2017-12-24 11:19:04
