所谓Treap,就是一种二叉查找树,而我们知道二叉查找树,相对来说比较容易形成最坏的链表情况,所以我们有一种数据结构来防止二叉查找树出现最坏情况,那就是Treap。
Treap=tree+heap,Treap就是这样一种既是树又是堆的奇怪的东东。我们每次插入节点时,便随机的给每个节点赋给一个值,我们要求原始数据满足二叉查找树的性质,而随机值要满足堆的性质。
比如下面的一棵树:
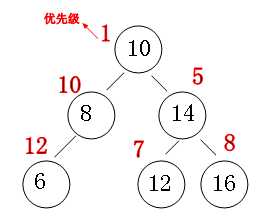
首先我们知道各个节点的“优先级”是采用随机数的方法,那么就存在一个问题,当我们插入一个节点后,优先级不满足“堆定义"的。那么我们就要旋转这课树。
①: 左左情况旋转
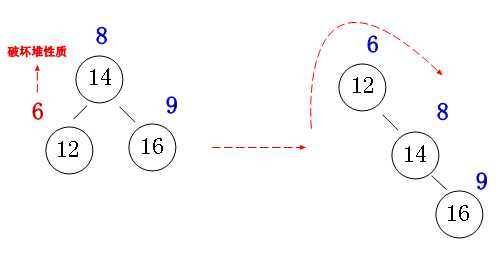
②: 右右情况旋转
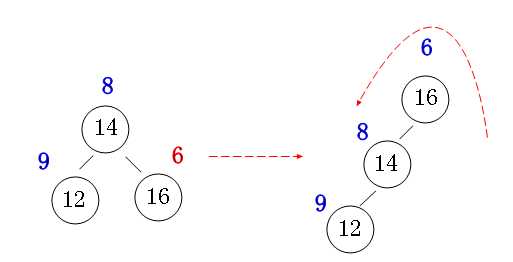
好在我们写一个旋转函数就可以同时维护左旋和右旋了:
void play(Treap* &rr,int d){ Treap *k=rr->ro[d^1]; rr->ro[d^1]=k->ro[d];//ro[0]是左孩子,ro[1]是右孩子 k->ro[d]=rr; rr->rub();//rub()函数的作用是重新统计该子树的大小 k->rub();//必须先rr再k,因为现在rr是k的孩子 rr=k; }
那么我们就可以刷水题了:(洛谷-普通平衡树)
#include<bits/stdc++.h> #define sight(c) (‘0‘<=c&&c<=‘9‘) #define RR NULL #define inf 1<<29 #define random rrsbRRsb using namespace std; inline int random(){ static int seed=707; return seed=int(seed*48271LL%2147483647); } struct Treap{ int key,rap,siz; Treap *ro[2]; Treap(int k){ siz=1; key=k; rap=random(); ro[1]=ro[0]=RR; } inline void rub() { siz=1; if (ro[0]!=RR) siz+=ro[0]->siz; if (ro[1]!=RR) siz+=ro[1]->siz; } inline int cop(int x){ if (x==key) return -1; return x<key?0:1; } }; inline void read(int &x) { static char c; static int b; for (b=1,c=getchar();!sight(c);c=getchar()) if (c==‘-‘) b=-1; for (x=0;sight(c);c=getchar()) x=x*10+c-48; x*=b; } void play(Treap* &rr,int d){ Treap *k=rr->ro[d^1]; rr->ro[d^1]=k->ro[d]; k->ro[d]=rr; rr->rub(); k->rub(); rr=k; } void Insert(Treap* &rr,int x){ if (rr==RR) rr=new Treap(x); else { int d=x < rr->key?0:1; Insert(rr->ro[d],x); if (rr->ro[d]->rap > rr->rap) play(rr,d^1); } rr->rub(); } bool Find(Treap *p,int x){ while(p!=RR) { int d=p->cop(x); if (d==-1) return true; p=p->ro[d]; } return false; } void Delete(Treap* &t,int x){ int d=t->cop(x); if (d==-1) { Treap *tmp=t; if (t->ro[0]==RR) { t=t->ro[1]; delete tmp; tmp=RR; } else if (t->ro[1]==RR) { t=t->ro[0]; delete tmp; tmp=RR; } else { int k=t->ro[0]->rap<t->ro[1]->rap?0:1; play(t,k); Delete(t->ro[k],x); } } else Delete(t->ro[d],x); if (t!=RR) t->rub(); } int Kth(Treap *t,int k){ int cm=0; if (t->ro[0]) cm=t->ro[0]->siz; cm++; if (cm==k) return t->key; if (cm>k) return Kth(t->ro[0],k); return Kth(t->ro[1],k-cm); } int Rank(Treap *t,int k){ int r; if (!t) return inf; if (t->ro[0]==RR) r=0;else r=t->ro[0]->siz; if(k==t->key) return min(r+1,Rank(t->ro[0],k)); if(k<t->key) return Rank(t->ro[0],k); return r+1+Rank(t->ro[1],k); } int Pre(Treap *t,int k){ if (!t) return -inf; if (k>t->key) return max(t->key,Pre(t->ro[1],k)); return Pre(t->ro[0],k); } int Sub(Treap *t,int k){ if (!t) return inf; if (k<t->key) return min(t->key,Sub(t->ro[0],k)); return Sub(t->ro[1],k); } int n,op,x; int main () { freopen("a.in","r",stdin); read(n); Treap* root=RR; while (n--) { read(op); read(x); switch(op){ case 1:Insert(root,x);break; case 2:Delete(root,x);break; case 3:printf("%d\n",Rank(root,x));break; case 4:printf("%d\n",Kth(root,x));break; case 5:printf("%d\n",Pre(root,x));break; case 6:printf("%d\n",Sub(root,x));break; } // cout<<op<<endl; } return 0; }
