整理3Blue1Brown的课程内容,方便随时翻看。
原视频地址:https://www.bilibili.com/video/av10308208/
要了解微积分的本质,我们从一个大家都知道的公式说起。这个公式就是求圆的面积公式:A=πr2
我们将用微积分的方式来推导这个公式,在这个过程中,我们将利用到微分,积分,和两者的互逆

首先我们先将一个圆如下图切分成数个圆环。我们获得每个圆环的面积,然后将他们相加不就得到圆的面积了。
所以我们以相同的距离dr将圆切分成若干个同心圆环。
比如圆环的半径是3,dr取0.1 那么我们就将一个圆换分成了30个宽度都是0.1的同心圆环:

每一个圆环拉直会得到一个新的形状,我们将这个形状近似看做一个矩形
那么这个矩形的面积就是这个圆环的周长乘以dr,圆环的周长为圆环到圆心的距离*2π
那么每个圆环的近似面积面积就为:2πr*dr(这里的r是每个圆环到圆心的距离)
你会发现我们的dr 取值越小,那么我们计算出来的圆的面积也就越精确。

现在如果我们把所有近似矩从小到大一个接一个的排列在一起,我们会有一些全新的发现:
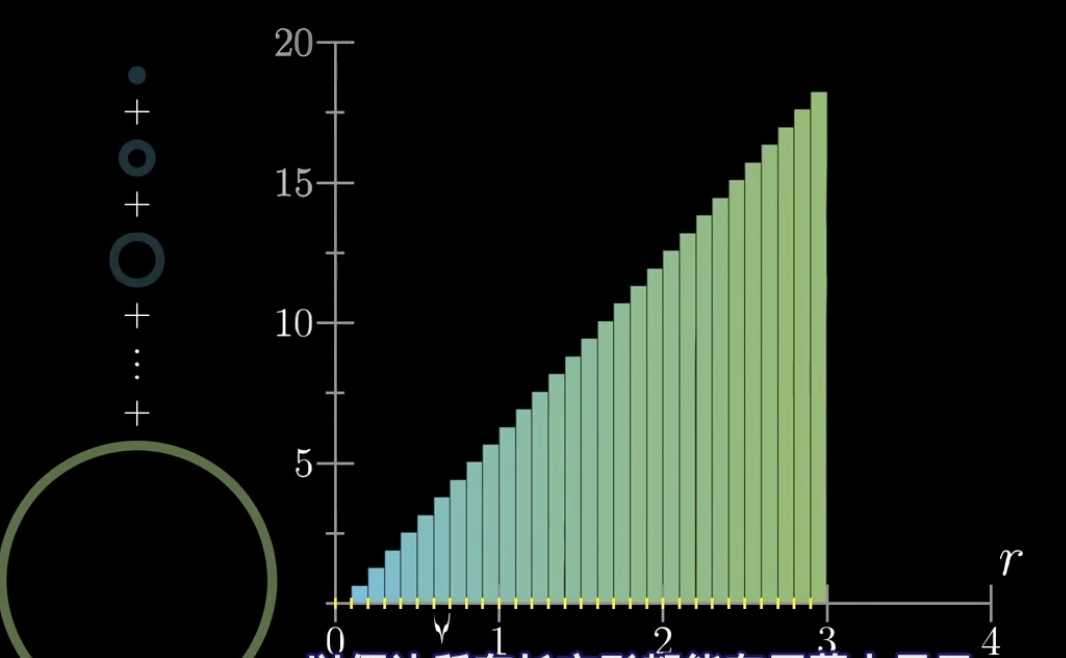
注意,为了方便观察我们y轴与x轴的比例为5:1
现在我们去的dr是0.1,而我们取的dr值越小,获得的圆环的数量就越多,而这些圆环的近似矩形面积相加起来的面积就靠近原来的圆的面积。
若是无限多个圆环,那么我们获得的近似值越来越靠近真实值。
可是我们取的圆环越多,那么计算量不就越大,无限多的就代表根本没法计算。
但注意,当dr取值无限小的时候,我们将所有圆环的面积加起来与下图三角形的面积是相同的。
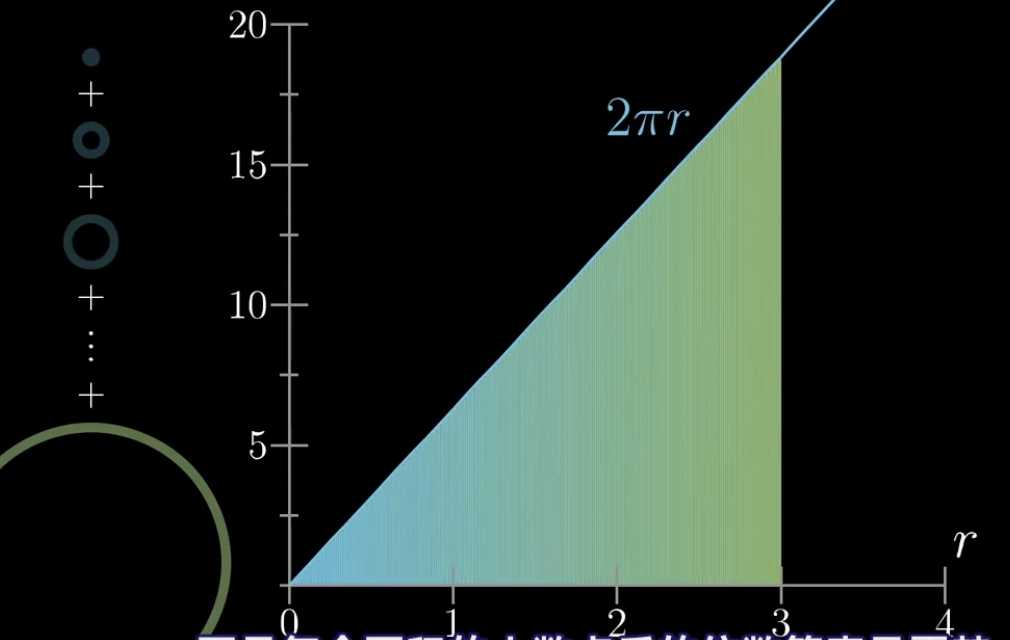
这个三角形的底是3 而高最大圆环的周长,也就是圆的周长:2π*3
如果圆的半径是r,那么它对应的三角形就是一个底为r,高为2π*r的三角形。根据三角形面积公式,我们得到
圆的面积为:πr2
对于数学家来说,你不光要找到答案,你还想要能发展处解决一般问题的工具和技巧
我们回想一下刚刚发生了什么。为什么这样做是可行的。这个从近似值到精确值的过程,通过这个过程,我们可以了解微积分的本质。
最开我们将问题化解为许多微小值的和,来获得一个近似的结果。
首先我们取每间隔dr值,取一个圆环。我们将一个圆换分成若干个小圆环,将其近似看成若干个矩形,我们就能获得近似的圆形面积。
这里的dr 不仅是圆环的宽度,也是每个圆环半径的间距。
我们将这个这个dr越缩小,dr值取的越小,所有矩形相加的面积就越接近于一个三角形的面积。
我们可以得出结论,原来的原型的面积恰好就是这个三角形的面积。
注意此时已经不是近似值,而是完全准确。
用这种方法,我们还可以解决一些其他的问题。
下一小节,我们看看这个方法是如何在其他问题上应用的。
