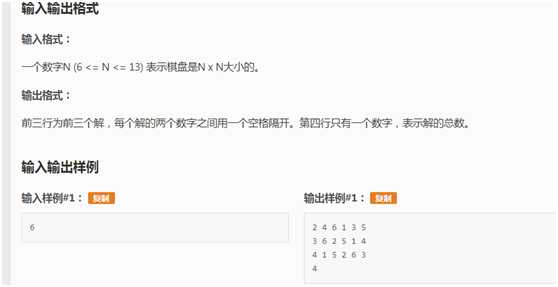
在一个n×n的棋盘上放置n个国际象棋中的皇后,要求所有的皇后之间都不形成攻击。请你给出所有可能的排布方案数。
输入格式
一个整数n
输出格式
方案数
经典的回溯题目。因为对于八皇后问题我们很难找到能够快速得到解的方法(嗯,那些10行写完的速度出门右拐)。所以我们采取枚举法。
皇后的攻击特性是,同行,同列,同一对角线。那么不妨先人为规定第k个皇后在第k行,这样就可以根据皇后的列号求解。
我们先把第1个皇后放在第1行第一列,然后再逐行递归。而这个搜索过程实际是在一棵搜索树上进行的
嗯,树太大不放出来就,百度据说一堆?
然后一个比较关键的问题是如何处理对角线
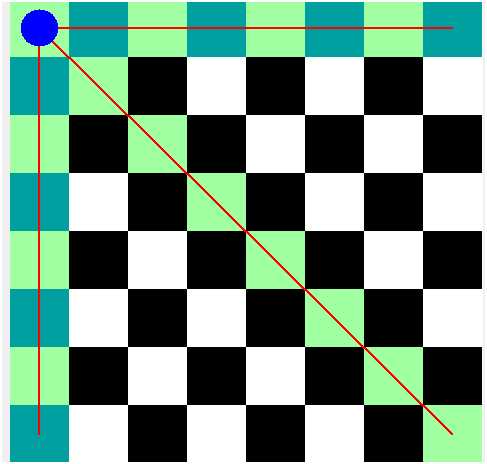
就比如说这样一个节点,如果用x表示行,y表示列,这个节点的右对角线就可以用
x-y+n
来表示,因为在这样一条对角线上,所以的点的横纵坐标都满足x-y+n
我们权且把它叫做这个点的右对角线
那么左对角线怎么办呢?
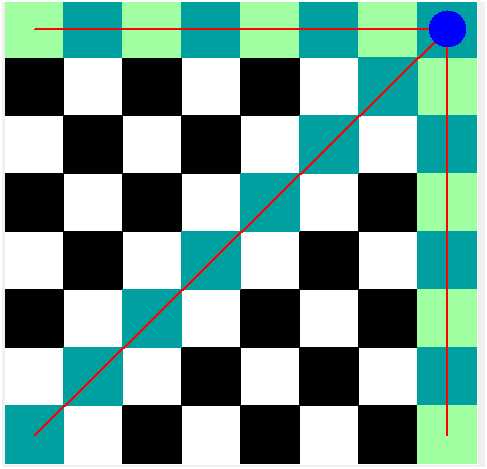
以这个点为例,同样设行用x表示,列用y表示,那么这个点的右对角线就是
x+y
所以在这条对角线上的点的坐标都满足这个式子。
那么接下来的问题就简单了,随便dfs,瞎标记就行了
代码如下:
#include <bits/stdc++.h>
using namespace std;
bool h[70],leftx[70],rightx[70];//h表示列,即不在同一列,leftx表示左对角线,rightx表示右对角线
int n,ans=0;
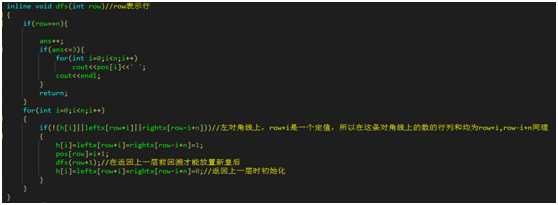
inline void dfs(int row)//row表示行
{
if(row==n){
ans++; return;
}
for(int i=0;i<n;i++)
{
if(!(h[i]||leftx[row+i]||rightx[row-i+n]))//左对角线上,row+i是一个定值,所以在这条对角线上的数的行列和均为row+i,row-i+n同理
{
h[i]=leftx[row+i]=rightx[row-i+n]=1;
dfs(row+1);//在返回上一层前回溯才能放置新皇后
h[i]=leftx[row+i]=rightx[row-i+n]=0;//返回上一层时初始化
}
}
}
int main()
{
cin>>n;
memset(h,0,sizeof(h));
memset(leftx,0,sizeof(leftx));
memset(rightx,0,sizeof(rightx));
dfs(0);
cout<<ans<<endl;
return 0;
}
而在usaco上,还有一道和这个差距不是很大的题,就差了几行代码

可以看出无非就是按照上面那个思路让在递归的前3层输出所有点的列,开一个数组记录一下列就好了
dfs代码如下: