视频链接:https://www.bilibili.com/video/av10396996/
这一节课,我们会用可视化的方式直观的思考导数公式的意义。
并鼓励你永远不要忘记,微小的变化才是导数的意义。
在一个公式f(x)中,当我们的x轴取值发生了dx的微小变化时,相应的在y轴产生了一个df的变化。
df/dx也就是这个变化的变化率。这就是导数的意义。
我们知道当f(x)=x2时,我们的变化率会随着x的增加而增加。
当x=0时,是切线斜率是0
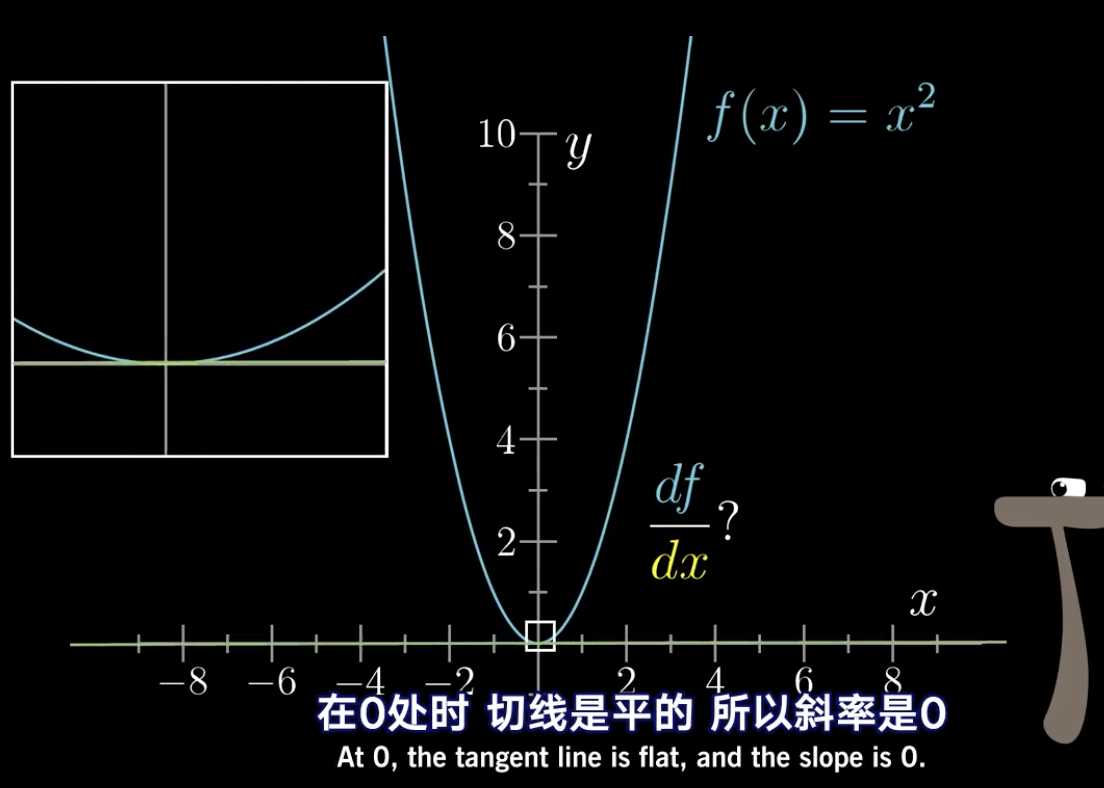
当x=1时,它的斜率稍微变得陡峭。
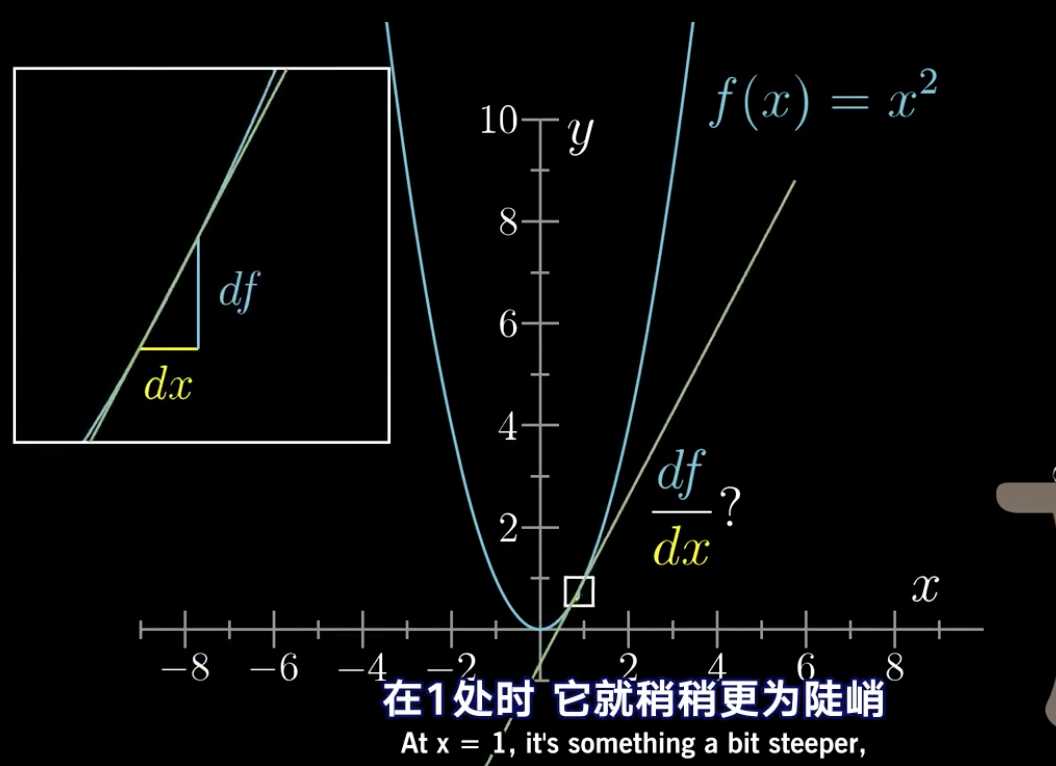
而随着x的增加,会越来越陡峭。
接下来我们用更直观的方式来理解。
x2,可以理解为一个边长为x的正方形面积。
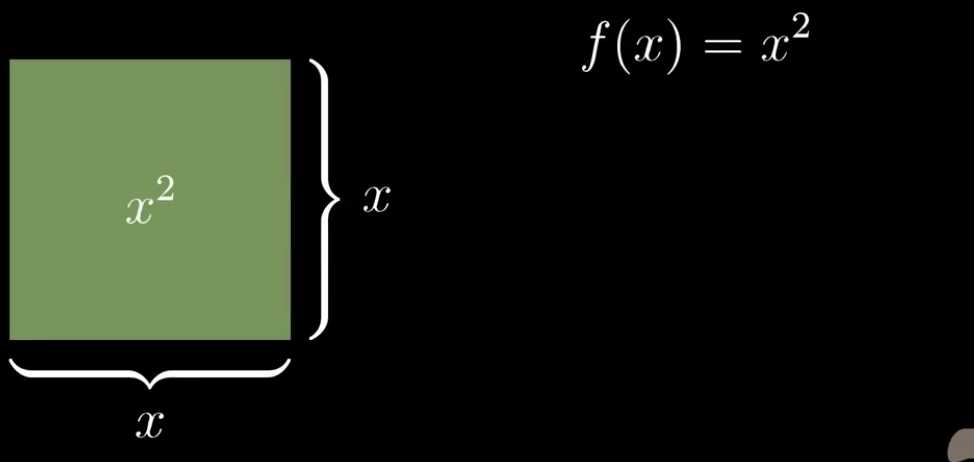
上图这个正方形,我们这个正方形设随着x增加的而增加的面积为df那么: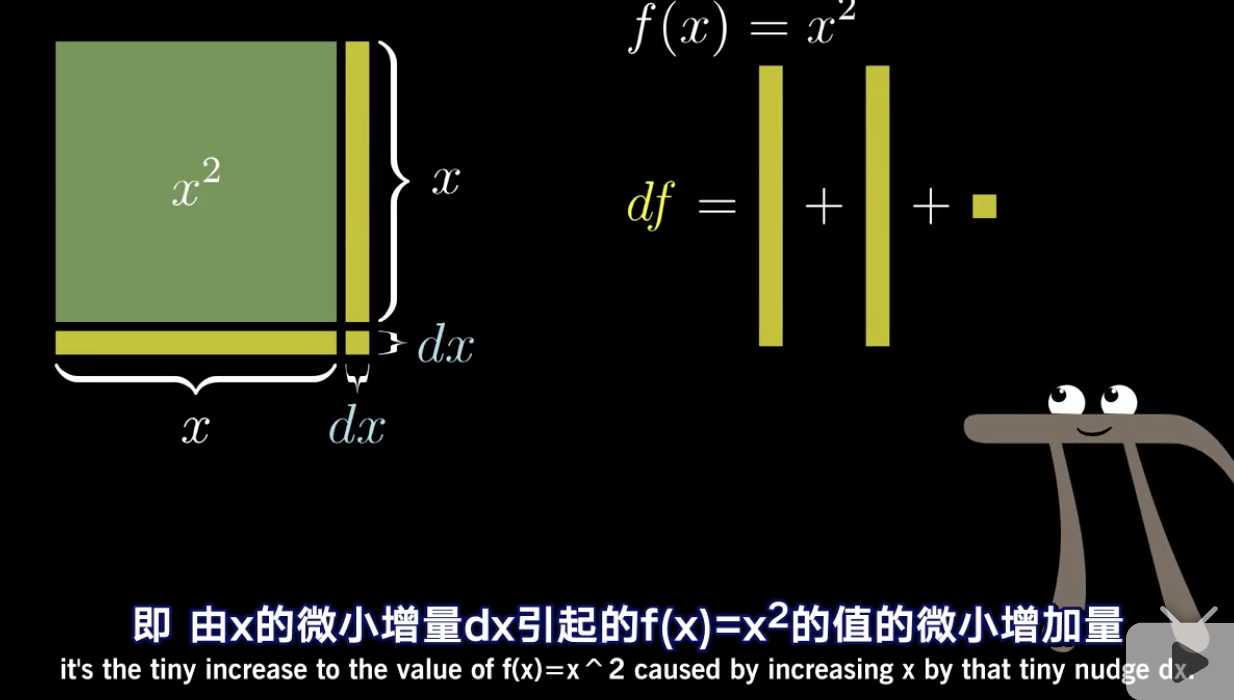
增加的面积为两个竖条的面积各自为:x*dx 而小方块的面积为: dx2
那么df=2x*dx+dx2
df/dx=2x + dx
当dx逐渐缩小,dx可以忽略不计。
我们就得到f(x2)的导数是 2x

同样的道理可以直观的推导到三次方的公式上。
x3理解为一个边长为x的立方体。
用上面的方法可以很容易的直观想象出,为什么x3求导公式是3x2
但是x三次方以上的幂函数我们很难用几何图形的方式想象他的形状。毕竟我们的大脑是在三维空间中进化来的。
一下就是x的n次幂求导公式的推导。虽然不能直接用集合图形法来证明,
但是把这个公式中的各个相加的项与我们之前公式中的项相对应,还是可以帮助你更好的理解这个推导的过程。
而且图像法也可以告诉我们,数学公式是有现实意义的,并非只是纯粹的计算技巧。

