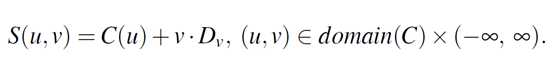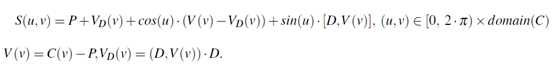OpenCASCADE构造一般曲面
Abstract. 本文主要介绍常见的曲面如一般柱面(拉伸曲面)、旋转面在OpenCASCADE中的构造方法,由此思考一般放样算法的实现。
Key Words. Common Surface, Extrusion, Revolution
1.Introduction
实体Solid就是由面组成,面中包含几何曲面,常见的几何曲面有平面,柱面,旋转面等。对几何曲面有一些功能要求:如计算指定参数u,v处的点,切线等,即求指定参数u,v处的0阶导数、1阶导数,N阶导数;获取参数空间等。
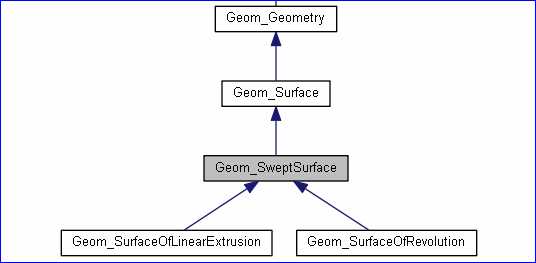
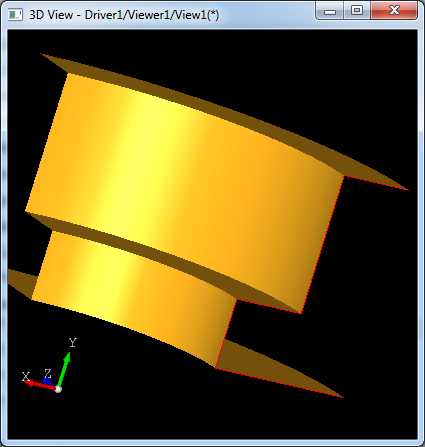
图1. 放样曲面
由类图可以看出,放样曲面Swept Surface有两种形式:Geom_SurfaceOfLinearExtrusion和Geom_SurfaceOfRevolution。一种是线性拉伸成形的曲面,一种是旋转成形的曲面。
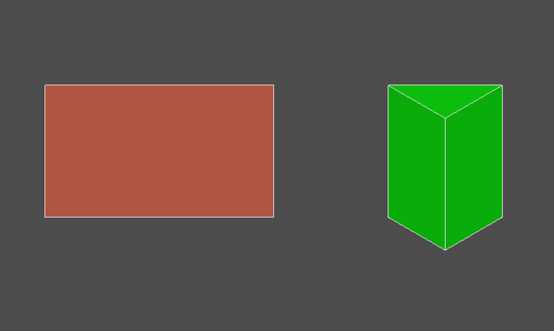
图2. 拉伸曲面
如上图1所示,可以将一条曲线沿一方向拉伸一定的距离来构造曲面,被拉伸的曲线称为准线。
图3. 旋转曲面
如上图2所示,将一条曲线绕指定的轴线旋转一定的角度得到一个旋转面。
本文结合OpenCASCADE中源码来说明拉伸曲面及旋转曲面原理。
2.The Surface of Extrusion
OpenCASCADE中线性拉伸曲面的类名为:Geom_SurfaceOfLinearExtrusion,其参数方程如下:
其中参数u的定义域决定准线C(u)的参数范围;参数v的取值范围是无穷的。即拉伸曲面是一个很长的柱面,如果在参数v上不加限制的话。其中一些计算功能代码如下所示:
//! Shift the point along direction to the given distance (theShift) void Shift(const Standard_Real theShift, gp_Pnt& thePoint) const { thePoint.ChangeCoord() += myDirection.XYZ() * theShift; } void GeomEvaluator_SurfaceOfExtrusion::D0( const Standard_Real theU, const Standard_Real theV, gp_Pnt& theValue) const { if (!myBaseAdaptor.IsNull()) myBaseAdaptor->D0(theU, theValue); else myBaseCurve->D0(theU, theValue); Shift(theV, theValue); }
从计算曲面上在指定参数u,v处的点的函数D0()可以看出,先根据参数u计算出准线上的点,再将点沿拉伸方向移动拉伸向量模的距离。
图4. 拉伸多边形
如上图4所示为将多边形准线沿着Z方向拉伸得到一个拉伸曲面。
3.The Surface of Revolution
OpenCASCADE中旋转曲面的类名为:Geom_SurfaceOfRevolution,其参数方程如下:
其中计算旋转曲面上对应参数u,v的点的代码如下:
void GeomEvaluator_SurfaceOfRevolution::D0( const Standard_Real theU, const Standard_Real theV, gp_Pnt& theValue) const { if (!myBaseAdaptor.IsNull()) myBaseAdaptor->D0(theV, theValue); else myBaseCurve->D0(theV, theValue); gp_Trsf aRotation; aRotation.SetRotation(myRotAxis, theU); theValue.Transform(aRotation); }
根据代码可知,先根据参数v计算曲线上的点,再将点按指定的轴旋转变换。
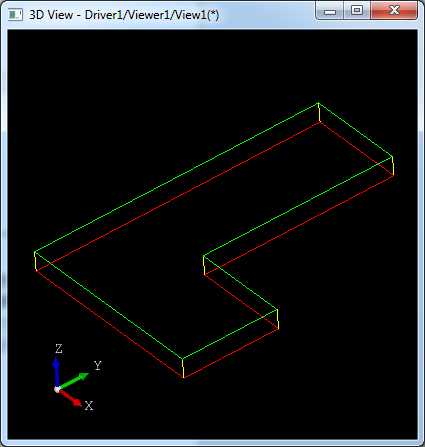
图5. 旋转曲面
如上图5所示,将红色母线绕Y轴旋转90度得到的旋转曲面。线性拉伸曲面和旋转曲面都是特定条件下的放样曲面。拉伸曲面为沿直线放样得到的曲面,旋转曲面是沿圆放样得到的曲面。由此,可以思考一个问题,那就是如何将任意一个曲面沿任意路径来放样构造曲面呢?
图6. 放样曲面