解:展开函数式得到2yx2+2xy+y=x2-2x-3
继而得到(2y-1)x2+(2y+2)x+(y+3)=0
将上式看作x的二次方程,y组成了方程的系数。
只有Δ>=0,x才有实值。
Δ=(2y+2)2-4(2y-1)(y+3)=-4y2-12y+16>=0
推导出(y+4)(y-1)<=0
满足条件的y在-4和1之间
下图是函数曲线,可见理论是符合实际的。
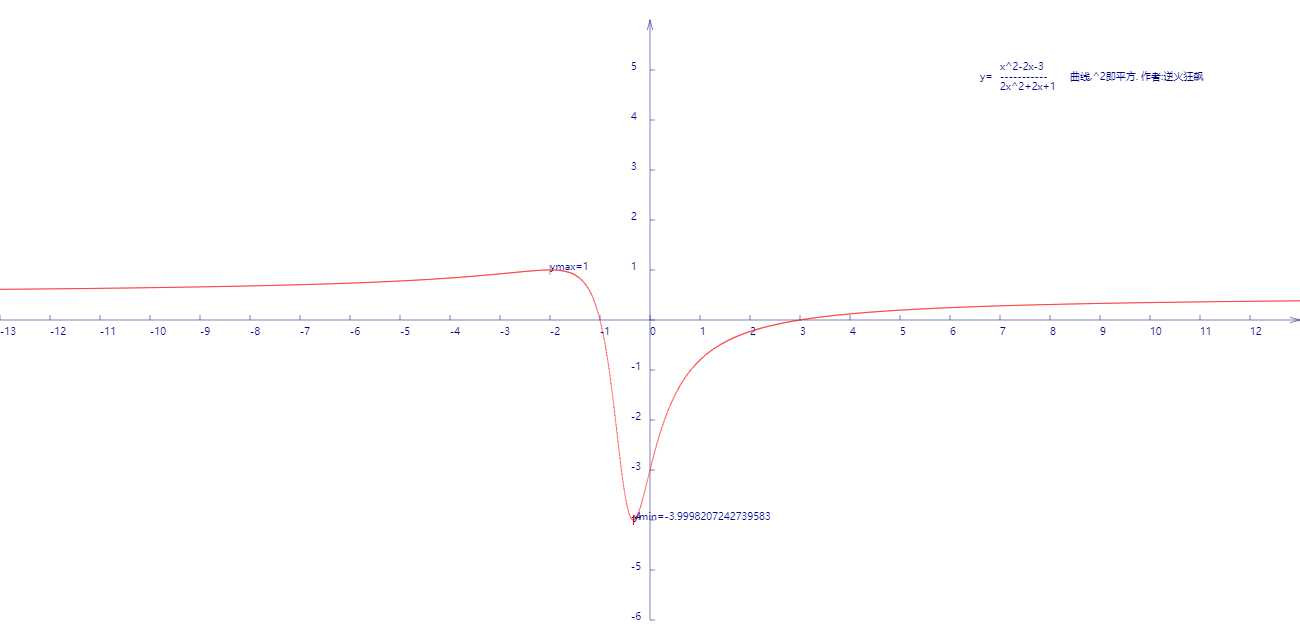
对于y=(a‘x2+b‘x+c‘)/(ax2+bx+c)类似的函数求极值,都可以用此判别法,注意a不可以为零,否则不可以用此方法判断极值,彼时该用算术平均值大于等于几何平均值的定理计算极值。
2017年12月28日
