一道好题。
我们考虑旋转和翻转的循环节个数就可以了。
先说旋转：
旋转应该是朝着一个方向从旋转1个到n个
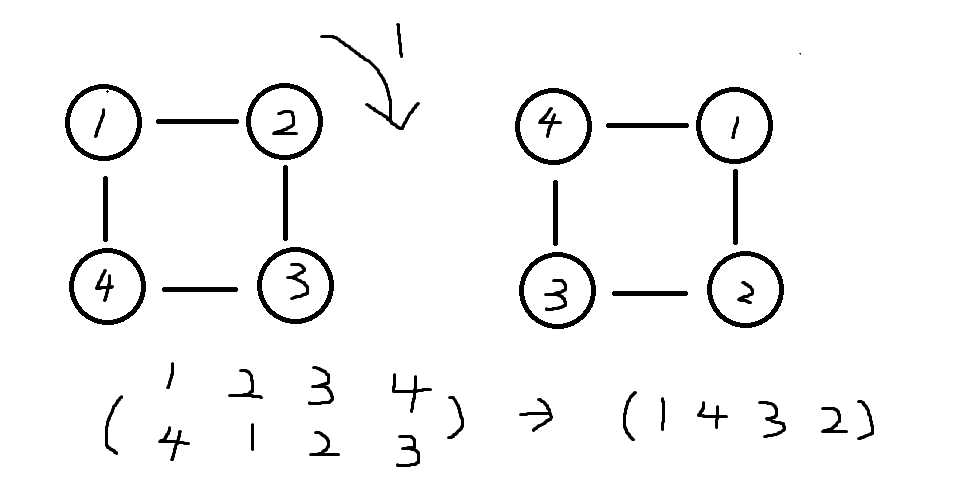此时循环节个数为1
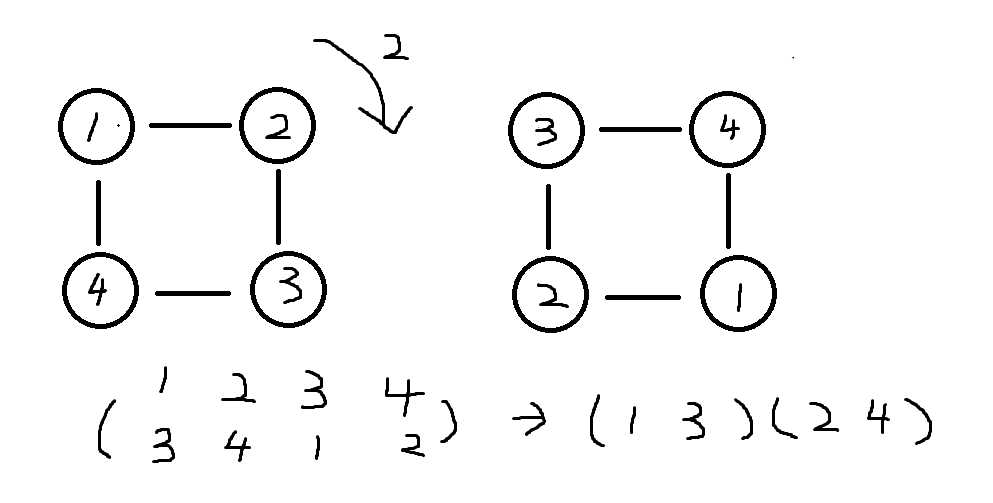此时循环节个数为2
从上面两个我们可以看出旋转长度为k时，循环节长度为lcm(n,k)/k,所以循环节个数为n/lcm(n,k)/k=gcd(n,k)
再说翻转：
考虑奇偶
奇：
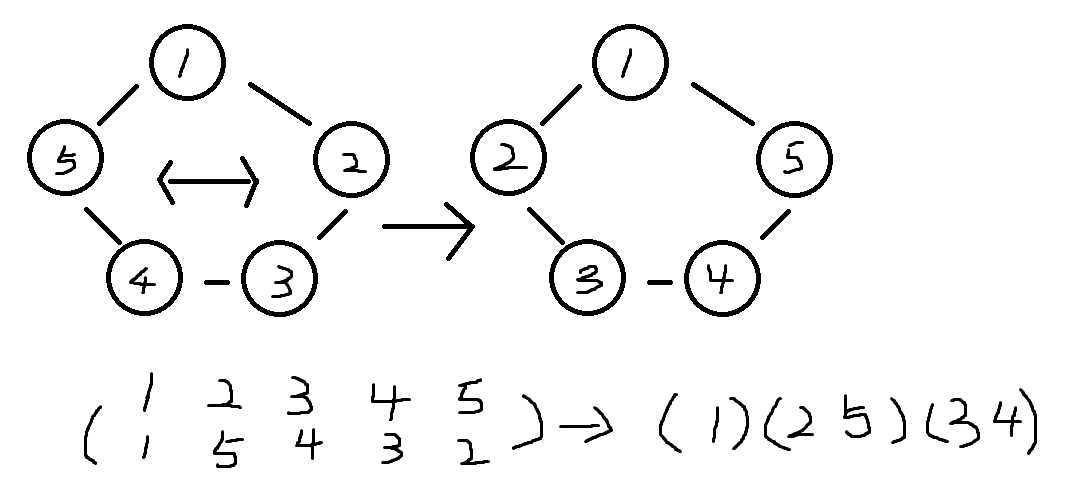循环节个数为3
共可以翻转n次循环节长度为n/2，所以循环节个数为(n+1)/2
偶：
分两种情况讨论
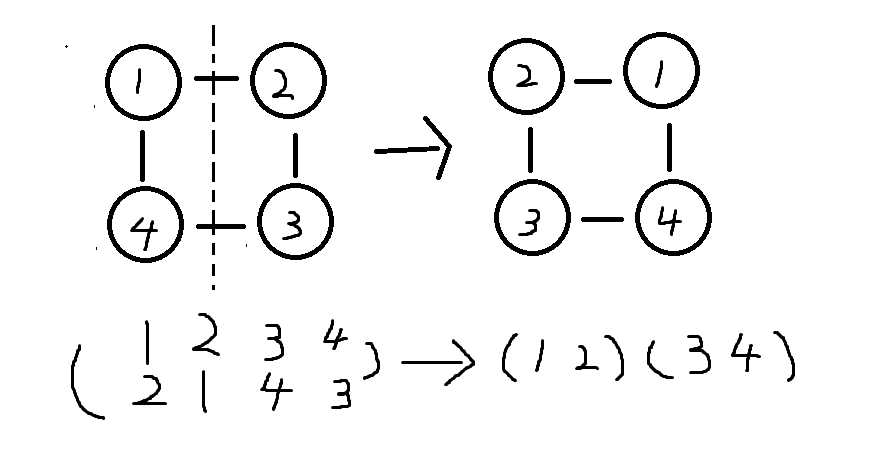循环节个数为2
共可以左右对称n/2次，循环节长度为2，循环节个数为n/2个
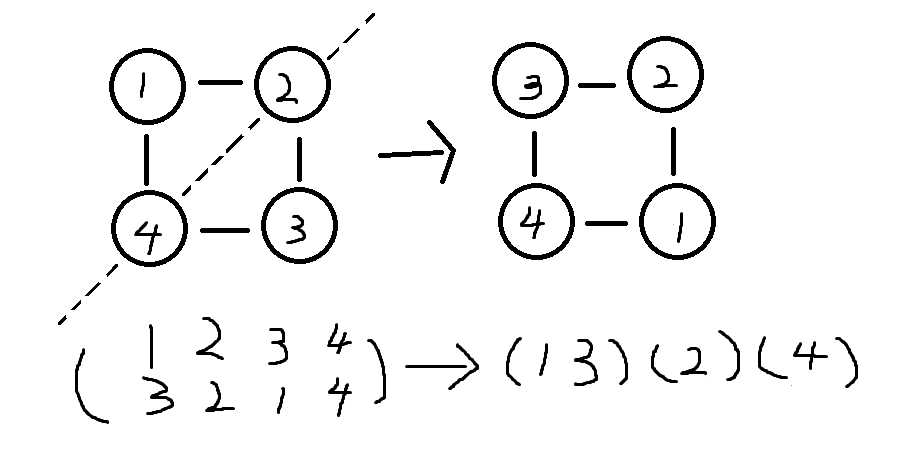循环节个数为3
共可以对角线对称n/2次，循环节长度为2，循环节个数为(n-2)/2+2个
所以到这里我们就把所有情况讨论了。
代码 By：大奕哥
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdlib> 4 #include<cstdio> 5 #include<cstring> 6 using namespace std; 7 int n,m,sum; 8 int gcd(int x,int y) 9 { 10 if(!y)return x; 11 return gcd(y,x%y); 12 } 13 int quick_mod(int a,int b) 14 { 15 int ans=1; 16 while(b) 17 { 18 if(b&1)ans=ans*a; 19 a=a*a;b>>=1; 20 } 21 return ans; 22 } 23 int main() 24 { 25 while(~scanf("%d%d",&m,&n)&&n&&m) 26 { 27 sum=0;for(int i=1;i<=n;++i)sum+=quick_mod(m,gcd(n,i)); 28 if(n&1)sum+=n*quick_mod(m,(n+1)/2); 29 else sum+=(n/2)*(quick_mod(m,n/2)+quick_mod(m,(n+2)/2)); 30 sum=sum/(n*2);printf("%d\n",sum); 31 } 32 return 0; 33 }
