朴素贝叶斯文本分类简单介绍

时间：2017-12-29 20:56:36 阅读：267 评论：0 收藏：0 [点我收藏+]

标签：ast 之间 logs -- mode rac possible class 回归

本文介绍朴素贝叶斯算法如何对文本进行分类。比如，每个用户的购物评论就是一篇文本，识别出这篇文本属于正向评论还是负面评论就是分类的过程，而类别就是：{正面评论，负面评论}。正面评论为Positive，用标识符‘+‘表示；负面评论为Negative，用标识符‘-‘表示。

一，分类目标

寻找文本的某些特征，然后根据这些特征将文本归为某个类。

The goal of classification is to take a single observation, extract some useful
features, and thereby classify the observation into one of a set of discrete classes.

使用监督式机器学习方法对文本进行分类：首先假设已经有分好类的N篇文档：(d₁,c₁)、(d₂,c₂)、(d₃,c₃)……(d_n,c_n)

d_i表示第i篇文档，c_i表示第i个类别。目标是：寻找一个分类器，这个分类器能够：当丢给它一篇新文档d，它就输出d （最有可能）属于哪个类别c

二，分类器的介绍

①Generative classifier

朴素贝叶斯分类器属于Generative classifier。　　

②Discriminative classifier

逻辑回归属于Discriminative classifier。

Generative classifiers like naive Bayes build a model of each class. Given an observation,they return the class most likely to have generated the observation. 
Discriminative classifiers like logistic regression instead learn what features from the input are most useful to discriminate between the different possible classes.

三，词袋模型（Bag Of Words）

前面提到，文本分类需要寻找文本的特征。而词袋模型就是表示文本特征的一种方式。给定一篇文档，它会有很多特征，比如文档中每个单词出现的次数、某些单词出现的位置、单词的长度、单词出现的频率……而词袋模型只考虑一篇文档中单词出现的频率(次数)，用每个单词出现的频率作为文档的特征（或者说用单词出现的频率来代表该文档）。词袋模型的示意图如下：

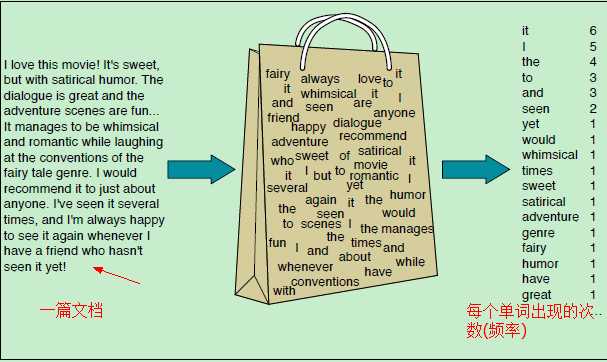
技术分享图片

We represent a text document as if it were a bag-of-words, 
that is, an unordered set of words with their position ignored, keeping only their frequency in the document.

四，朴素贝叶斯分类器

朴素贝叶斯分类器是一个概率分类器。假设现有的类别C={c₁，c₂，……c_m}。给定一篇文档d，文档d最有可能属于哪个类呢？这个问题用数学公式表示如下：

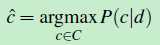技术分享图片（公式一）

c^{^}就是：在所有的类别C={c₁，c₂，……c_m} 中，使得：条件概率P(c|d)取最大值的类别。使用贝叶斯公式，将（公式一）转换成如下形式：

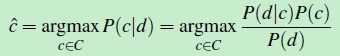技术分享图片 (公式二)

对类别C中的每个类型，计算 [p(d|c)*p(c)]/p(d) 的值，然后选取最大值对应的那个类型c_i ，该c_i就是最优解c^{^}，因此，可以忽略掉分母 p(d)，（公式二）变成如下形式：

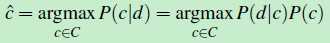技术分享图片 (公式三)

这个公式由两部分组成，前面那部分P(d|c) 称为似然函数，后面那部分P(c) 称为先验概率。

前面提到使用词袋模型来表示文档d，文档d的每个特征表示为：d={f₁,f₂,f₃……f_n}，那么这里的特征f_i其实就是单词w_i出现的频率（次数），公式三转化成如下形式：

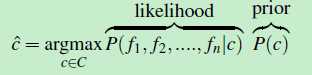技术分享图片 (公式四)

对文档d 做个假设：假设各个特征之间是相互独立的。那么p(f₁,f_2……f_n|c)=p(f₁|c)*p(f₂|c)*……*p(f_n|c)，公式四转化成如下形式：

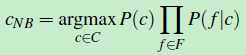技术分享图片（公式五）

由于每个概率值很小（比如0.0001）若干个很小的概率值直接相乘，得到的结果会越来越小。为了避免计算过程出现下溢(underflower)，引入对数函数Log，在 log space中进行计算。然后使用词袋模型的每个单词w_i 出现频率作为特征，得到如下公式

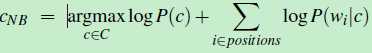技术分享图片（公式六）

五，训练朴素贝叶斯分类器

训练朴素贝叶斯的过程其实就是计算先验概率和似然函数的过程。

①先验概率P(c)的计算

P(c)的意思是：在所有的文档中，类别为c的文档出现的概率有多大？假设训练数据中一共有N_doc篇文档，只要数一下类别c的文档有多少个就能计算p(c)了，类别c的文档共有N_c篇，先验概率的计算公式如下：

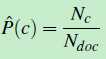技术分享图片 (公式七)

【先验概率其实就是准备干一件事情时，目前已经掌握了哪些信息了】关于先验信息理解，可参考：这篇文章。

For the document prior P(c) we ask what percentage of the documents in our training set are in each class c. 
Let Nc be the number of documents in our training data with
class c and Ndoc be the total number of documents

②似然函数P(w_i|c)的计算

由于是用词袋模型表示一篇文档d，对于文档d中的每个单词w_i，找到训练数据集中所有类别为c的文档，数一数单词w_i在这些文档（类别为c）中出现的次数：count(w_i,c)

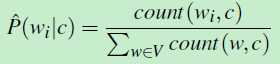然后，再数一数训练数据集中类别为c的文档一共有多少个单词技术分享图片。计算二者之间的比值，就是似然函数的值。似然函数计算公式如下：

技术分享图片（公式八）

其中V，就是词库。（有些单词在词库中，但是不属于类别C，那么 count(w,c)=0）

Here the vocabulary V consists of the union of all the word types in all classes, not just the words in one class c.

从上面计算似然函数的过程来看，其实相当于一个发掘（统计）潜藏规律的过程。

六，unknow words的情形

假设只考虑文本二分类：将文档分成 positve类别，或者negative类别，C={positive, negative}

在训练数据集中，类别为positive的所有文档都没有包含单词w_i = fantastic（fantastic可能出现在类别为negative的文档中）

那么 count(w_i=fantastic，c_i=positive)=0 。那么：

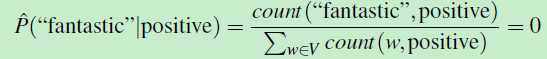
技术分享图片

而注意到前面公式五中的累乘，整篇文档的似然函数值为0，也就是说：如果文档d中有个单词fantastic在类别为c的训练数据集文档中从未出现过，那文档d被分类到类别c的概率为0，尽管文档d中还有一些其他单词（特征），而这些单词所代表的特征认为文档d应该被分类到类别c中

But since naive Bayes naively multiplies all the feature likelihoods together, zero
probabilities in the likelihood term for any class will cause the probability of the
class to be zero, no matter the other evidence!

解决方案就是 add-one smoothing。（不介绍了），其实就是将“出现次数加1”。似然函数公式变成如下形式：

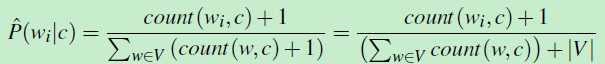技术分享图片（公式九）

其中|V|是词库中所有单词的个数。

七，朴素贝叶斯分类示例

假设训练数据集有五篇文档，其中Negative类别的文档有三篇，用符号 ‘-‘ 标识；Positive类别的文档有二篇，用符号 ‘+‘ 标识，它们的内容如下：

-  just plain boring
-  entirely predictable and lacks energy
-  no surprises and very few laughs


+  very powerful
+  the most fun film of the summer

测试数据集T 有一篇文档d_t，内容如下：