前缀和心得

今天做牛客网西南民大的题遇到了二维前缀和的题目，是个比较经典出过很多次的题目了，

看来光掌握一维前缀和还是远远不够的，二维前缀和也必须很熟练。

前缀和

前缀和可以理解为数学上的数列的前n项和（对于一个一维数组的前缀和）。

我们定义一个数组a的前缀和数组sum[i]=a[1]+a[2]+...+a[i],一般用for循环从1遍历到n，sum[i]=sum[i-1]+a[i].有点DP的意味，从前一个推出后一个。将中间结果保存下来, 避免重复计算, 用以提高运算效率。

int init() {
    for(int i = 1; i <= n; i++) sum[i] = sum[i-1] + a[i];
}
int get(int l, int r) {
    return sum[r] - sum[l-1];
}

二维前缀和

与一维前缀和类似，设sum[i][j]表示所有a[i‘][j‘]（1≤i‘≤i,1≤j‘≤j）的和。

有一点像“矩形的面积”那样，把一整块区域的值都加起来。

前缀和的用途

一般用来求区间和。

对于一维的情况，现在给你一个数列a，要求你回答m次询问，每次询问下标j到k的和。朴素的做法显然是对于每一次询问都执行一次相加操作，然后输出结果。这样做是对的，但是m过大的时候就会导致计算次数过多而超时。

超时的原因一目了然，重复计算。那么我们应该如何改进方案呢？想象一下，我们如果提前计算好了每一个位置的前缀和，再用s[k]-s[j]，结果不就是我们这次询问的答案吗！这样使得计算量大大减小。

对于二维区间和也是类似的。

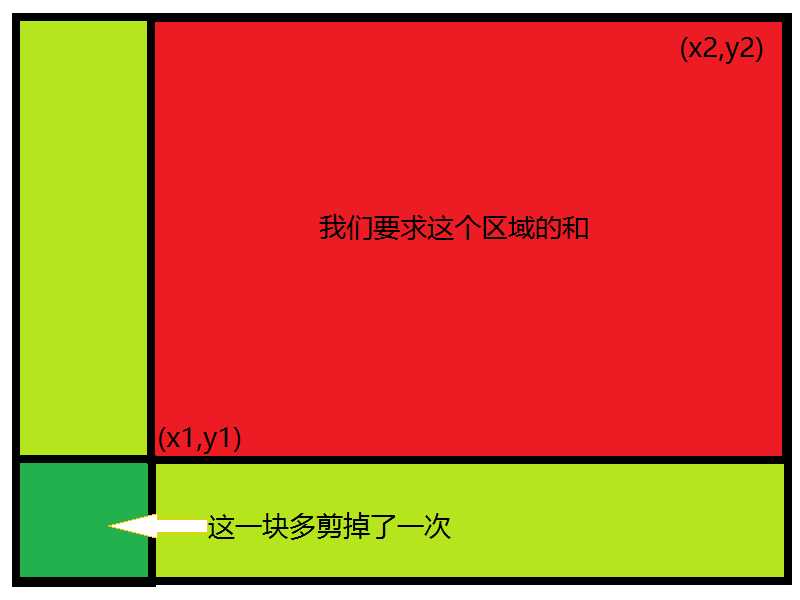
借助这个图片。假设在这个矩阵（二维数组）中，我们要求和的是上图中红色区域。现在我们已经预处理好了所有点的前缀和。现在给定两个点（x1，y1），（x2，y2）。我们要求以这两个点连线为对角线的一个子矩阵的数值之和。暴力法为直接挨个相加，早晚的TLE。考虑前缀和的快速做法。

首先可以把s[x2][y2]求出来，它代表整个大矩形的前缀和，然后我们分别减去左边多的一块前缀和和下边多出来的一块前缀和，但这还不是最终答案！显然，当我们减去两个多余的区间时，下边的一小块被减了两次，应该加回来。

所以对一次查询的答案ans为s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]

这个二维前缀和也称为差分序列。

int init() {
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + a[i][j];
        }
    }
}
int get(int x1, int y1, int x2, int y2) {
    return sum[x1][y1] - sum[x1][y2 - 1] - sum[x2 - 1][y1] + sum[x2 - 1][y2 - 1];
}

应用问题 

核心就两个字：降维。

面对许多高维问题，往往前缀和是最先想到的降维方法。 
这样在降维的基础上，许多更进一步的优化才能实现。

【推荐题目】：

1.http://acm.hdu.edu.cn/showproblem.php?pid=5084 hdu 5084 前缀和预处理 

/*
如图，a[2][2]的前缀和就是2+3+2+7，a[1][4]的前缀和就是2+3+4+8 
以此类推，每一个坐标的前缀和，都是该坐标到矩阵左上角的数字之和； 
这样，任意子矩阵的数字和，可以在O（1）时间内查询； 
*/ 
for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        b[i][j]+=b[i][j-1];

 for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        b[i][j]+=b[i-1][j];//计算前缀和