数学软件实训任务二
一 题目:MATLAB程序综合设计及应用
二 目的:熟练掌握MATLAB程序设计的基本方法,会根据MATLAB程序设计的
三 要求:
1 熟练掌握控制流的基本语法结构。
2 会熟练应用for循环,while循环及分支语句if …else和switch…case等进行混合编程,处理实际问题。
四 实训内容:
1 方程求根的二分法及程序设计
(1)方程求根的二分法的基本原理
取[a,b]的中点$\xi \displaystyle _{1}=\frac{a+b}{2}$,计算 $f(\xi _{1})$.
如果$f(\xi _{1})=0$;那么$\xi=\xi_{1}$;
如果 $f(\xi _{1})$与$f(a)$同号,那么取$a_{1}=\xi_{1}$,$b_{1}=b$,由$f(a_{1})*f(b_{1})<0$,即知$a_{1}<\xi <b_{1}$,且$b_{1}-a_{1}=\frac{b-a}{2}$;
如果$f(\xi _{1})$与$f(b)$同号,那么取$a_{1}=a,b_{1}=\xi _{1}$,由$f(a_{1})*f(b_{1})<0$,即知$a_{1}<\xi <b_{1}$,且$b_{1}-a_{1}=\frac{b-a}{2}$;
总之,当$\xi \neq \xi_{1}$时,可求得$a_{1}<\xi<b_{1}$,且$b_{1}-a_{1}=\frac{b-a}{2}$.
以[a1,b1]作为新的隔离区间,重复上述做法,当$\xi\neq\xi_{2}=\frac{a_{1}+b_{1}}{2}$时,可求得
$a_{2}<\xi <b_{2}$,且$b_{2}-a_{2}=\frac{b-a}{2^{2}}$.
如此重复n次,可求得$a_{n}<\xi<b_{n} $,$b_{n}-a_{n}=\frac{b-a}{2^{n}}$.由此可知,如果以$a_{n}$或$b_{n}$作为$\xi$的近似值,那么其误差小于$\frac {b-a} {2^{n}}$.如图14-23是二分法的原理示意图.
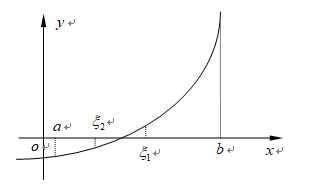
图 14-23 二分法原理示意图
二分法的优点是对函数的要求低(只要求满足零点定理的条件),方法简便、可靠,程序设计容易,事先估计次数容易,收敛速度恒定。
(2)二分法程序设计
(3)绘出函数$f(x)=x^{3}+1.1x^{2}+0.9x-1.4$的图像,找出根的隔离区间,然后用所编写的二分法程序求方程$f(x)=x^{3}+1.1x^{2}+0.9x-1.4=0$实根的近似值,使误差不超过$10^{-3}$.
