题目背景
跑步是一项有意思的运动,尤其是可以开发人的脑筋。常神牛很喜欢跑步。
题目描述
常神牛跑步的场地是一个多边形(边数≤20,每个顶点用英文大写字母表示),并且在这个多边形内部,还会有一些小道,连接两个不相邻的顶点。所有的边长和小道都是双向通行的举例来说,下面一个图:
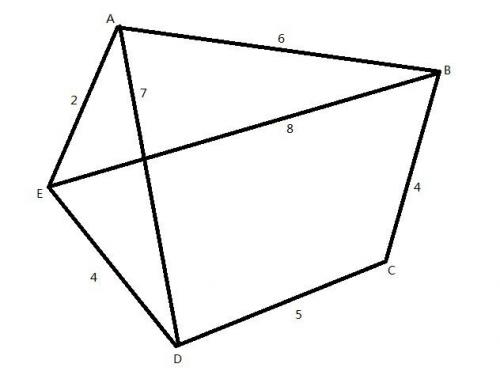
假设常神牛从A点跑到D点,最短的路径是A-E-D(长度为6)。
现在告诉你多边形的边数n,多边形每条边的长度,多边形内的连线数k,每条连线的两个端点及长度,以及起始点和结束点,请你输出最短路径的长度。但是常神牛有点强迫症,如果两点之间有多条道路直接连接,他会选择最长的那条。
注意:输入数据不保证起点和终点不同,也不保证小道的起点和终点不同。在读入过程中,如果两点之间有多条小道,那么它们间的距离为这些小道的最大值。所以,如果读入一个小道起点和终点相同,那么这个点到它本身的距离不为0。
输入输出格式
输入格式:
输入文件为run.in。
第一行,2个数,n,k。
第二行,n个数,分别表示多边形每条边的长度(按顺时针次序依次给出,即分别为AB,BC,CD,DE……的长度)。
以下k行,每行两个字母和一个数,两个字母表示该连线的起止点,数字表示长度。
最后一行,两个字母,分别为他跑步的起点和终点。
所有的一行的字母、数字之间用一个空格隔开。
输出格式:
输出文件为run.out。
一行,一个数,表示最短路的长度。
输入输出样例
说明
对于20%的数据,k=0;
对于50%的数据,k≤10;
对于100%的数据,1≤n≤20,0≤m≤50,k≤100,所有路径长度均不大于1000。
思路:这是我第一次跪在scanf上,用scanf输入竟然会RE简直不可思议。floyed最短路即可。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 30 using namespace std; int n,k; int map[MAXN][MAXN]; int main(){ memset(map,0x3f,sizeof(map)); scanf("%d%d",&n,&k); for(int i=1;i<=n;i++){ int x; scanf("%d",&x); map[i][i%n+1]=map[i%n+1][i]=x; } for(int i=1;i<=k;i++){ char a,b;int x; cin>>a>>b>>x; if(map[a-‘A‘+1][b-‘A‘+1]<1000) map[a-‘A‘+1][b-‘A‘+1]=map[b-‘A‘+1][a-‘A‘+1]=max(map[a-‘A‘+1][b-‘A‘+1],x); else map[a-‘A‘+1][b-‘A‘+1]=map[b-‘A‘+1][a-‘A‘+1]=x; } for(int i=1;i<=n;i++) if(map[i][i]>1000) map[i][i]=0; for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i!=j&&i!=k&&j!=k&&map[i][j]>map[i][k]+map[k][j]) map[j][i]=map[i][j]=map[i][k]+map[k][j]; char a,b; cin>>a>>b; cout<<map[a-‘A‘+1][b-‘A‘+1]; }
