目录
数据可视化
梯度下降
结果可视化
|
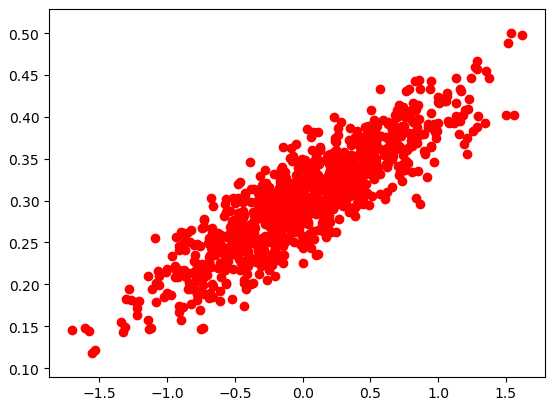
数据可视化 |
import numpy as np import tensorflow as tf import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围 num_points = 1000 vectors_set = [] for i in range(num_points): x1 = np.random.normal(0.0, 0.55) y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03) vectors_set.append([x1, y1]) # 生成一些样本 x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] plt.scatter(x_data,y_data,c=‘r‘) plt.show()
|
梯度下降 |
# -*- coding: utf-8 -*- import numpy as np import tensorflow as tf import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围 num_points = 1000 vectors_set = [] for i in range(num_points): x1 = np.random.normal(0.0, 0.55) y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03) vectors_set.append([x1, y1]) # 生成一些样本 x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] # 生成1维的W矩阵,取值是[-1,1]之间的随机数 W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name=‘W‘) # 生成1维的b矩阵,初始值是0 b = tf.Variable(tf.zeros([1]), name=‘b‘) # 经过计算得出预估值y y = W * x_data + b # 以预估值y和实际值y_data之间的均方误差作为损失 loss = tf.reduce_mean(tf.square(y - y_data), name=‘loss‘) # 采用梯度下降法来优化参数 optimizer = tf.train.GradientDescentOptimizer(0.5) #参数是学习率 # 训练的过程就是最小化这个误差值 train = optimizer.minimize(loss, name=‘train‘) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) # 初始化的W和b是多少 print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) # 执行20次训练 for step in range(20): sess.run(train) # 输出训练好的W和b print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) ‘‘‘ W = [ 0.72134733] b = [ 0.] loss = 0.204532 W = [ 0.54246926] b = [ 0.31014919] loss = 0.0552976 W = [ 0.41924465] b = [ 0.30693138] loss = 0.029155 W = [ 0.33045709] b = [ 0.30471471] loss = 0.0155833 W = [ 0.26648441] b = [ 0.30311754] loss = 0.00853772 W = [ 0.22039121] b = [ 0.30196676] loss = 0.00488007 W = [ 0.18718043] b = [ 0.3011376] loss = 0.00298124 W = [ 0.16325161] b = [ 0.30054021] loss = 0.00199547 W = [ 0.14601055] b = [ 0.30010974] loss = 0.00148373 W = [ 0.13358814] b = [ 0.29979959] loss = 0.00121806 W = [ 0.12463761] b = [ 0.29957613] loss = 0.00108014 W = [ 0.11818863] b = [ 0.29941514] loss = 0.00100854 W = [ 0.11354206] b = [ 0.29929912] loss = 0.000971367 W = [ 0.11019413] b = [ 0.29921553] loss = 0.00095207 W = [ 0.10778191] b = [ 0.29915532] loss = 0.000942053 W = [ 0.10604387] b = [ 0.29911193] loss = 0.000936852 W = [ 0.10479159] b = [ 0.29908064] loss = 0.000934153 W = [ 0.1038893] b = [ 0.29905814] loss = 0.000932751 W = [ 0.10323919] b = [ 0.2990419] loss = 0.000932023 W = [ 0.10277078] b = [ 0.29903021] loss = 0.000931646 W = [ 0.10243329] b = [ 0.29902178] loss = 0.00093145 ‘‘‘
|
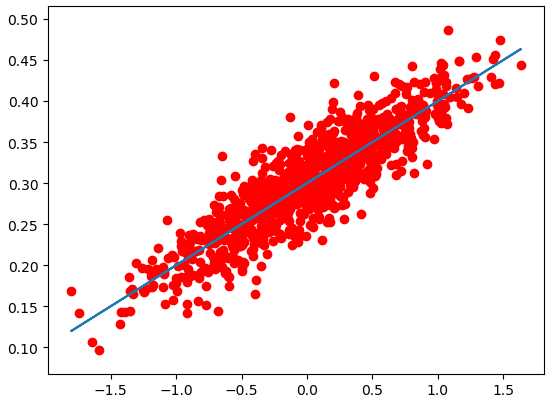
结果可视化 |
# -*- coding: utf-8 -*- import numpy as np import tensorflow as tf import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围 num_points = 1000 vectors_set = [] for i in range(num_points): x1 = np.random.normal(0.0, 0.55) y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03) vectors_set.append([x1, y1]) # 生成一些样本 x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] # 生成1维的W矩阵,取值是[-1,1]之间的随机数 W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name=‘W‘) # 生成1维的b矩阵,初始值是0 b = tf.Variable(tf.zeros([1]), name=‘b‘) # 经过计算得出预估值y y = W * x_data + b # 以预估值y和实际值y_data之间的均方误差作为损失 loss = tf.reduce_mean(tf.square(y - y_data), name=‘loss‘) # 采用梯度下降法来优化参数 optimizer = tf.train.GradientDescentOptimizer(0.5) #参数是学习率 # 训练的过程就是最小化这个误差值 train = optimizer.minimize(loss, name=‘train‘) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) # 初始化的W和b是多少 print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) # 执行20次训练 for step in range(20): sess.run(train) # 输出训练好的W和b print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) plt.scatter(x_data,y_data,c=‘r‘) plt.plot(x_data,sess.run(W)*x_data+sess.run(b)) plt.show()