题目大意 一个人打游戏,需要不超过$R$秒通过$n$关,第$i$关有$P_{i}$的概率用$F_{i}$秒通过,$\left(1 - P_{i}\right)$的概率用$S_{i}$通过($F_{i} < S_{i}$),通过每一关可以选择重置游戏,然后从头开始,或者去打下一关。问不超过$R$秒通过所有关卡的期望耗时。
转移是显然的。(如果这个都不会,请自定百度“概率dp入门题”)
然后发现转移有环,还要做决策?
然后列方程吧。。开心地发现不会解。
可惜这里是信息学竞赛,不是数学竞赛。由于转移都需要 dp[0][0] 但是开始不知道它,所以考虑二分它,然后和推出来的 dp[0][0] 作比较。
经过各种瞎猜和乱搞,可以发现一个神奇的事情
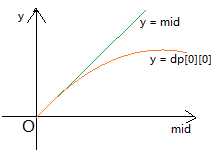
然后就可根据它来确定一次check后,二分的范围。
另外,由于坑人的精度问题,所以最好不要写while (l + eps < r) ,总之我这么写各种因为精度问题的TLE来了。
Code
1 /** 2 * Codeforces 3 * Problem#866C 4 * Accepted 5 * Time: 62ms 6 * Memory: 4316k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const long double eps = 1e-9; 13 const int binary_lim = 80; 14 15 int n, R; 16 int *fs, *ss; 17 double *ps; 18 19 inline void init() { 20 scanf("%d%d", &n, &R); 21 fs = new int[(n + 1)]; 22 ss = new int[(n + 1)]; 23 ps = new double[(n + 1)]; 24 for(int i = 1; i <= n; i++) { 25 scanf("%d%d", fs + i, ss + i); 26 cin >> ps[i]; 27 ps[i] *= 0.01; 28 } 29 } 30 31 boolean vis[51][5105]; 32 double f[51][5105]; 33 34 double dfs(int d, int t, double &mid) { 35 if(d == n) return (t > R) ? (mid) : (0); 36 if(vis[d][t]) return f[d][t]; 37 vis[d][t] = true; 38 f[d][t] = (dfs(d + 1, t + fs[d + 1], mid) + fs[d + 1]) * ps[d + 1] + (dfs(d + 1, t + ss[d + 1], mid) + ss[d + 1]) * (1 - ps[d + 1]); 39 if(mid < f[d][t]) f[d][t] = mid; 40 return f[d][t]; 41 } 42 43 double dp(double mid) { 44 memset(vis, false, sizeof(vis)); 45 return dfs(0, 0, mid); 46 } 47 48 inline void solve() { 49 double l = 0, r = 1e9; 50 for(int i = 0; i < binary_lim; i++) { 51 double mid = (l + r) / 2; 52 if(dp(mid) < mid) r = mid; 53 else l = mid; 54 } 55 printf("%.9lf", l); 56 } 57 58 int main() { 59 init(); 60 solve(); 61 return 0; 62 }

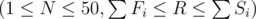 , the number of levels and number of seconds you want to complete the game in, respectively.
, the number of levels and number of seconds you want to complete the game in, respectively. 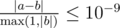 .
.