给定一个二分图G(V,E),V为顶点集,E为边集,在G的一个子图M中,M的边集E中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
求二分图最大匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)。
在这里我们主要讲解匈牙利算法。生活中,一个二分图最大匹配的典型应用是男女配对问题。假设有N个男生和M个女生,一个男生可以同时喜欢一个或者多个女生,当然也可以不喜欢任何女生。“喜欢”这种关系可以通过图模型来构建,若男生i和女生j互相喜欢,则在含有N+M个顶点的图中,存在一无向条边i--j。在上述图中,求解通过怎样的配对安排,使得配对的人数最多。
匈牙利算法框架
1. 初始化子图M为空
2. 若找到一个增广路径P,通过取反操作可以获得更多匹配数的子图M‘,M=M‘
3. 重复步骤2直到无法找到一个增广路径
何谓增广路径?
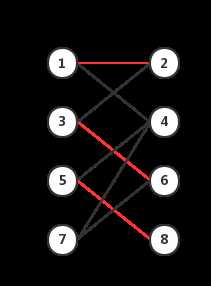
上图红色的三条边(1,2),(3,6),(5,8)为已经匹配的三条边。顶点7为未匹配点,从该点开始,找到一条路径:
7-->6-->3-->2-->1-->4
该路径即为一条增广路径(红色标记的为匹配边,黑色的为未匹配边)。增广路径有如下性质:
- 非匹配边和匹配边交替出现,其长度必定为奇数,且非匹配边比匹配边多一条
- 路径的起点和终点都是非匹配点(起点和终点不是同一个点)
- M为G的最大匹配当且仅当不存在相对于M的增广路径
利用性质“增广路径的非匹配边比匹配边多一条”,然后将非匹配边和匹配边反转,就可以不断增加匹配点和匹配边。上图反转后的结果图如下:
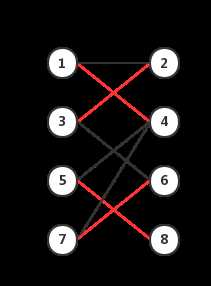
不断迭代,直到不能找到增广路径,即得到最大匹配(增广路定理)。
bool g[1011][1011]; bool isVisited[1011]; //标记点i是否被访问过 int matched[1011]; //表示点i匹配到的在另一边的点的编号int n, m; //分别表示左边和右边顶点的个数 bool DFS(int u){ for(int i = 1; i <= m; i++){ if(g[u][i] && !isVisited[i]){ isVisited[i] = true; if(!matched[i] || DFS(matched[i])){ //如果点i没有被访问或者从点matched[i]出发可以找到一条在增广路径 matched[i] = u;//设置匹配的点为u return true; } } } return false; } int maxMatch(){ int res = 0; memset(matched, 0, sizeof matched); for(int i = 1; i <= n; i++){ memset(isVisited, 0, sizeof isVisited); if(DFS(i)) res++; } return res; }
个人理解:匈牙利算法在理解上还是很直观的。假设遍历左边的点,对于第i个点,接着逐一访问与点i相连的右边的点,若右边的点为未访问状态,则开始访问。若该点,假设为点s,还未配对,则直接将该点与i配对;若已配对,则查看与s已经配对的点j是否可以改变配对对象而让i与s配对,这就是找增广路径的过程。当点j无法改变配对对象s时,则表示已经达到最大二分匹配。
