Description
米特是D星球上一种非常神秘的物质，蕴含着巨大的能量。在以米特为主要能源的D星上，这种米特能源的运输和储
存一直是一个大问题。D星上有N个城市，我们将其顺序编号为1到N，1号城市为首都。这N个城市由N-1条单向高速
通道连接起来，构成一棵以1号城市（首部）为根的树，高速通道的方向由树中的儿子指向父亲。树按深度分层：
根结点深度为0，属于第1层；根结点的子节点深度为1，属于第2层；依此类推，深度为i的结点属于第i+l层。建好
高速通道之后，D星人开始考虑如何具体地储存和传输米特资源。由于发展程度不同，每个城市储存米特的能力不
尽相同，其中第i个城市建有一个容量为A[i]的米特储存器。这个米特储存器除了具有储存的功能，还具有自动收
集米特的能力。如果到了晚上六点，有某个储存器处于未满的状态，它就会自动收集大气中蕴含的米特能源，在早
上六点之前就能收集满；但是，只有在储存器完全空的状态下启动自动收集程序才是安全的，未满而又非空时启动
可能有安全隐患。早上六点到七点间，根节点城市（1号城市）会将其储存器里的米特消耗殆尽。根节点不会自动
搜集米特，它只接受子节点传输来的米特。早上七点，城市之间启动米特传输过程，传输过程逐层递进：先是第2
层节点城市向第1层（根节点城市，即1号城市）传输，直到第1层的储存器满或第2层的储存器全为空；然后是第3
层向第2层传输，直到对于第2层的每个节点，其储存器满或其予节点（位于第3层）的储存器全为空；依此类推，
直到最后一层传输完成。传输过程一定会在晚上六点前完成。
由于技术原因，运输方案需要满足以下条件：
(1)不能让某个储存器到了晚上六点传输结束时还处于非空但又未满的状态，这个时候储存器仍然会启动自动收集
米特的程序，而给已经储存有米特的储存器启动收集程序可能导致危险，也就是说要让储存器到了晚上六点时要么
空要么满；
(2)关于首都——即1号城市的特殊情况， 每天早上六点到七点间1号城市中的米特储存器里的米特会自动被消耗
殆尽，即运输方案不需要考虑首都的米特怎么运走；
(3)除了1号城市，每个节点必须在其子节点城市向它运输米特之前将这座城市的米特储存器中原本存有的米特全部
运出去给父节点，不允许储存器中残存的米特与外来的米特发生混合；
(4)运向某一个城市的若干个来源的米特数量必须完全相同，不然，这些来源不同的米特按不同比例混合之后可能
发生危险。
现在D星人已经建立好高速通道，每个城市也有了一定储存容量的米特储存器。为了满足上面的限制条件，可能需
要重建一些城市中的米特储存器。你可以，也只能，将某一座城市（包括首都）中屎来存在的米特储存器摧毁，再
新建一座任意容量的新的米特储存器，其容量可以是小数（在输入数据中，储存器原始容量是正整数，但重建后可
以是小数），不能是负数或零，使得需要被重建的米特储存器的数目尽量少。
Input
第一行是一个正整数N，表示城市的数目。接下来N行，每行一个正整数，其中的第i行表示第i个城市原来存在的米
特储存器的容量。再接下来是N-I行，每行两个正整数a，b表示城市b到城市a有一条高速通道(a≠b)。
N<500000，A[j]<10^8
Output
输出文件仅包含一行，一个整数，表示最少的被重建（即修改储存器容量）的米特储存器的数目。
Sample Input
5
5
4
3
2
1
1 2
1 3
2 4
2 5
5
4
3
2
1
1 2
1 3
2 4
2 5
Sample Output
3
HINT
【样例解释】
一个最优解是将A[1]改成8，A[3]改成4，A[5]改成2。这样，2和3运给1的量相等，4和5运给2的量相等，且每天晚上六点的时候，1，2满，3，4，5空，满足所有限制条件。
题目大意
给一棵树，每个点有一个权值，要求修改一些点的权值，使得：
①同一个父亲的儿子权值必须相同
②父亲的取值必须是所有儿子权值之和
题解
有这样一个结论，当这棵树的任何一个节点的权值确定之后，其余所有节点的权值便都可算出来。
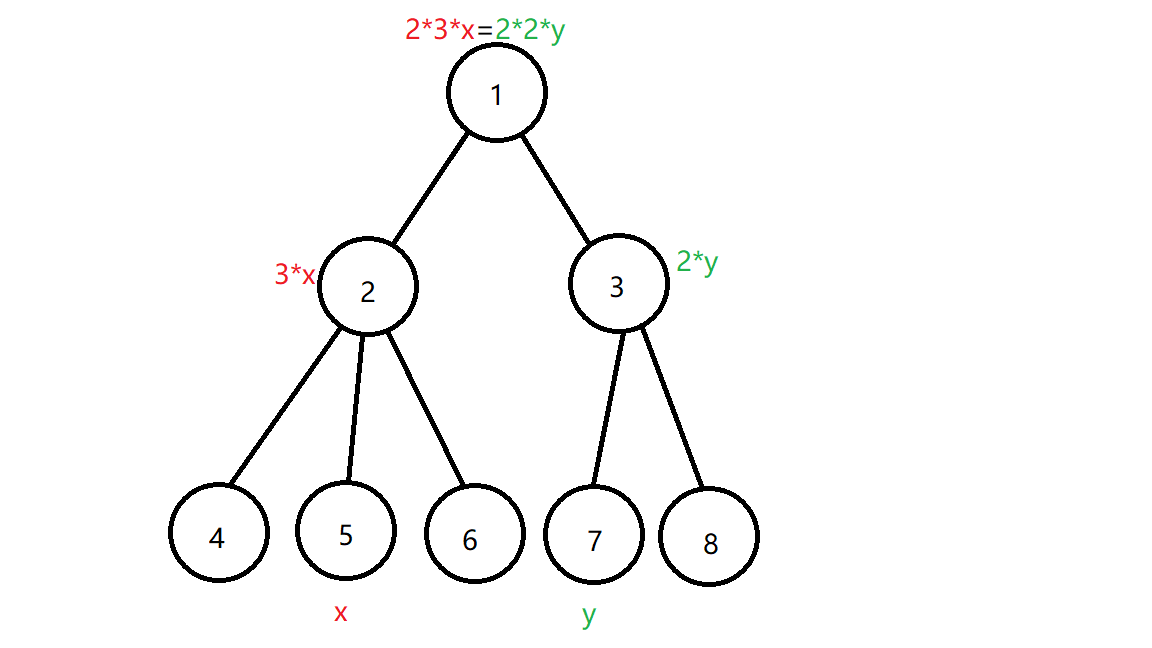
例如下图：
若我们确定了 $5$ 号节点的权值为 $x$ ，那么 $7$ 号节点的权值 $y$ 可以算出 $y = \frac{3}{2} \cdot x$ 。
现在我们将每一条边定向，方向为从父亲指向儿子，对于每个节点，统计每个节点的出度，做一遍树上前缀积 $prod_u$ 。例如上图中 $prod_5 = 6$ ， $prod_7 = 4$ ，特别地 $prod_1 = 1$ 。
我们假设 $u$ 节点的权值是不变的，那么必然有修改后的根节点的权为 $w = a_u \cdot prod_u$。
记 $f_u = prod_u*a_u$ ，我们将树上 $f_u$ 相同的点放在一组，现在问题就变成了求点数最多的一组的点的个数。
由于乘积过大，直接 $hash$ 。
1 //It is made by Awson on 2018.1.3 2 #include <set> 3 #include <map> 4 #include <cmath> 5 #include <ctime> 6 #include <queue> 7 #include <stack> 8 #include <cstdio> 9 #include <string> 10 #include <vector> 11 #include <cstdlib> 12 #include <cstring> 13 #include <iostream> 14 #include <algorithm> 15 #define LL long long 16 #define LD long double 17 #define Max(a, b) ((a) > (b) ? (a) : (b)) 18 #define Min(a, b) ((a) < (b) ? (a) : (b)) 19 using namespace std; 20 const int N = 500000; 21 const int MOD1 = 1e6+9; 22 const int MOD2 = 1e6+7; 23 const int MOD3 = 1e6-3; 24 25 int a[N+5], u, v, n; 26 struct tt { 27 int to, next; 28 }edge[(N<<1)+5]; 29 int path[N+5], top, degree[N+5]; 30 int hash1[MOD1+5], hash2[MOD2+5], hash3[MOD3+5]; 31 int ans1, ans2, ans3; 32 33 void add(int u, int v) { 34 edge[++top].to = v; 35 edge[top].next = path[u]; 36 path[u] = top; 37 } 38 void dfs(int u, int fa, int num1, int num2, int num3) { 39 int tmp, d = --degree[u]; 40 tmp = ++hash1[(LL)num1*a[u]%MOD1], ans1 = Max(ans1, tmp); 41 tmp = ++hash2[(LL)num2*a[u]%MOD2], ans2 = Max(ans2, tmp); 42 tmp = ++hash3[(LL)num3*a[u]%MOD3], ans3 = Max(ans3, tmp); 43 for (int i = path[u]; i; i = edge[i].next) 44 if (edge[i].to != fa) dfs(edge[i].to, u, (LL)num1*d%MOD1, (LL)num2*d%MOD2, (LL)num3*d%MOD3); 45 } 46 void work() { 47 scanf("%d", &n); 48 for (int i = 1; i <= n; i++) scanf("%d", &a[i]); 49 for (int i = 1; i < n; i++) { 50 scanf("%d%d", &u, &v); 51 add(u, v), add(v, u); ++degree[u], ++degree[v]; 52 } 53 ++degree[1]; 54 dfs(1, 0, 1, 1, 1); 55 printf("%d\n", n-Min(Min(ans1, ans2), ans3)); 56 } 57 int main() { 58 work(); 59 return 0; 60 }
