https://www.luogu.org/problemnew/show/3455#sub
http://www.lydsy.com/JudgeOnline/problem.php?id=1101
Description
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a
,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
Input
第一行包含一个正整数n,表示一共有n组询问。(1<=n<= 50000)接下来n行,每行表示一个询问,每行三个
正整数,分别为a,b,d。(1<=d<=a,b<=50000)
Output
对于每组询问,输出到输出文件zap.out一个正整数,表示满足条件的整数对数。
Sample Input
4 5 2
6 4 3
Sample Output
3
2
——————————————————————————————
因为莫比乌斯反演才学,所以都是先看神犇博客再做。
预备知识:
1.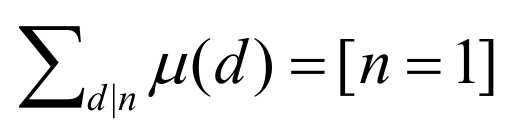
(而且hzw的博客有数学公式,我没有,所以不是特别好看,想看更加易懂的题解就戳上面吧。)
这题让你求∑∑[gcd(x,y)==d](x<=a,y<=b)的值。
显然可以化成∑∑[gcd(x,y)==1](x<=a/d,y<=b/d)
有知识1可得∑∑∑miu(c)(x<=a/d,y<=b/d,c|gcd(x,y))
又因为d|gcd(x,y)导出c|x&&c|y所以x可取值个数为a/d/c,b为b/d/c(都为整除,下同)。
所以可得∑miu(c)*a/d/c*b/d/c(c<=a/d&&c<=b/d)提取公因式得a/d/c*b/d/c*∑miu(c)。
将a/d看作整体,我们发现a/d/c又可以套用[CQOI2007]余数之和的方法分块,将复杂度减少至根号a/d。
#include<cstdio> #include<queue> #include<cctype> #include<cstring> #include<cmath> #include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int N=50010; int miu[N],su[N],sum[N]; bool he[N]; void Euler(int n){ int tot=0; miu[1]=1; for(int i=2;i<=n;i++){ if(!he[i]){ su[++tot]=i; miu[i]=-1; } for(int j=1;j<=tot;j++){ if(i*su[j]>=n)break; he[i*su[j]]=1; if(i%su[j]==0){ miu[i*su[j]]=0;break; } else miu[i*su[j]]=-miu[i]; } } for(int i=1;i<=n;i++)sum[i]=sum[i-1]+miu[i]; return; } int solve(int a,int b){ if(a>b)swap(a,b); int ans=0,pos; for(int i=1;i<=a;i=pos+1){ pos=min(a/(a/i),b/(b/i)); ans+=(sum[pos]-sum[i-1])*(a/i)*(b/i); } return ans; } int main(){ Euler(50001); int t; scanf("%d",&t); while(t--){ int a,b,d; scanf("%d%d%d",&a,&b,&d); printf("%d\n",solve(a/d,b/d)); } return 0; }
